《算法笔记》—— "迷宫求解" 之 深度优先搜索（DFS）

走过路过的小伙伴们，点个赞再走呗 ^ _ ^，你的支持是我前进的动力
迷宫相关算法文章：
《算法笔记》—— “迷宫求解” 之 广度优先搜索（BFS）

何为DFS？
简单点来说就是 在某一时刻，列出它的所有可能性，即当下需要干什么 . . .

---

废话不多说，我们以实例来讲解 DFS的使用.
我们需要做的求解迷宫的出路，利用DFS来求解 . . .

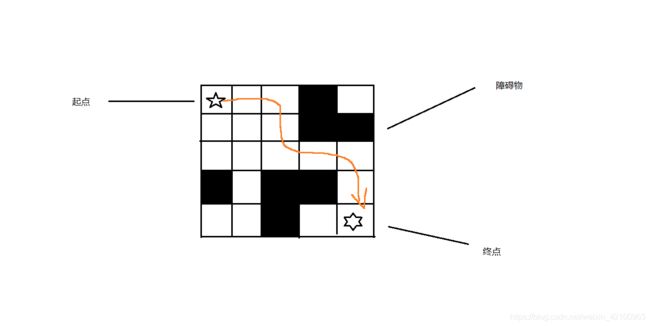
例如下图所示：

我画出的就是一种可以解出迷宫的路线，当然利用DFS可以解出更多的路线，此文章不会深究…

下面我会将起点称之为 A，终点称之为 B.

我们很容易的知道，当A每走一步时，他都有四个方向可以选择，这就是我开头所说的，他在这一时刻有四个可能性发生，当A以一种可能性移动时，他在当前又有四个可能性，这里小伙伴们应该容易的想到，这是一种递归的原理，当然他的终止条件就是 A 找到 B 了 . . .

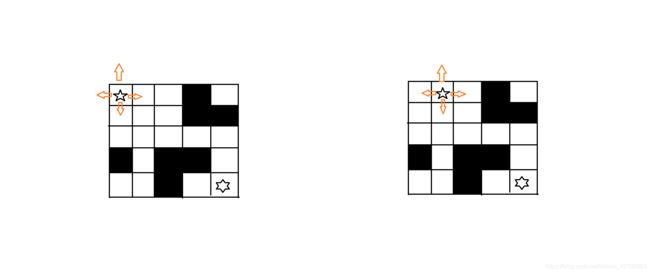
原理如下图所示：

当起点向右迈出一步时，它的可能性又有四种，同理，当起点向下迈出一步时，也有四种可能性.

聪明的小伙伴会发现，上面的图是会有越位的可能性，越位就是指 A 出去迷宫了，当然这种可能性是不允许的，我们只需要一个判断即可 . . .
我们也会发现，当 A 移动了一步时，当的所选可能性是有一个后退的方向，这种情况我们可以标记出这些位置已经走过了，避免重复的可能性 . . .

.

现在我们所知道的有：

1. A 每走一个位置都有四个方向所选择（当前点的所有可能性）
2. A 走过的路需要标记
3. 判断 A是否越界
4. 需要终止条件
5. 递归思想

.

好了，当我们知道这些东西时，就差不多理解了 DFS的基本原理 . . .
下面让我们来试一下 DFS如此写出来吧

---

.

DFS 代码解析

1. 函数封装 A 的当前位置，递归思想

void dfs(int x, int y)
{
}

2. 终止条件

void dfs(int x, int y)
{
    if(x == 4 && y == 4)	// B 的位置我们假设为 4，4
    {
        Yes = 1;		// 用于标记已经找到
        return;			// ************必须指定返回语句************
    }
}

3. 需要探索的四个方向，顺时针方向

// A 的横纵坐标的变化

int direction[4][2] = {
   0, 1,
   1, 0,
   0, -1,
   -1, 0
};

4. 获取 A 的四个方向的可能性

for(; i < 4; i++) // 4种方向  
{
    int nx = x + direction[i][0];  // 当前探索的方向 
    int ny = y + direction[i][1];
}

5. *********** 核心部分，递归思想 ***********

for(; i < 4; i++) // 4种方向  
{
    int nx = x + direction[i][0];  // 当前探索的方向 
    int ny = y + direction[i][1];
  
    // 判断 A 的当前位置是否已经出去迷宫了	
    if(nx < 0 || ny < 0 || nx > 4 || ny > 4)
        continue; 
        
    // 当前的路没有走过、并且当前的路不是障碍物    
    if(flag[nx][ny] == 0 && map[nx][ny] == 0)
    {
       flag[nx][ny] = 1;	// 走过的路标记
       dfs(nx, ny);		// 递归思想，当前步的下一步
       flag[nx][ny] = 0;	// ******当前步取消标记，用于上一步换个方向继续探索******
    } 
}

我相信 flag[nx][ny] = 0; 这一句大家应该会有点迷惑，下面我通过画图来解释这句代码的意思.

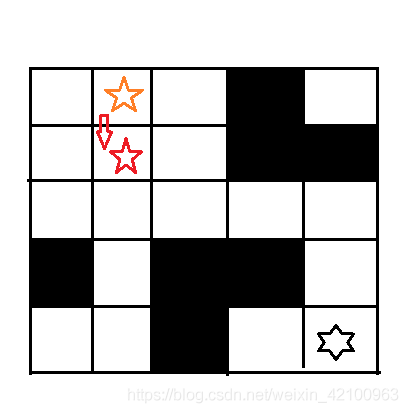
例如下图所示：

• 首先我们将 A 向下移动到 红色星星的位置
  

这时我们已经将 红色星星的位置标记为已经走过了 . . .
.

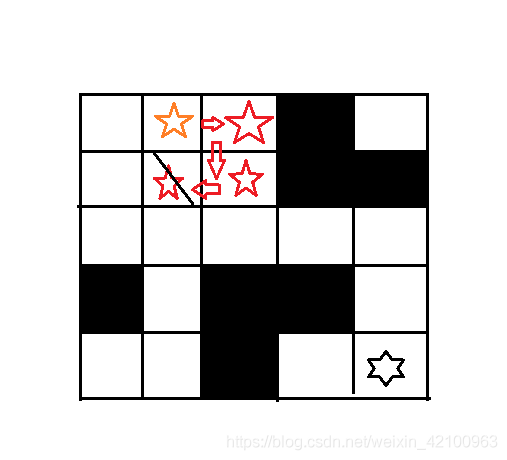
2. 我们将 A 继续向右边探索，将有如下的可能性

如果我们不把第一步向下的可能性走过的路取消掉，那么其它的所有可能性都不能再走 . . .

.

---

DFS其实就是将所有可能性，通过当下需要干什么的思想来进行完成 . . .

DFS核心的思想就是递归的使用，栈的原理，和二叉树的前序、后序遍历一个方式 . . .
此处可以看看我一篇文章：红黑树基本功能 —— C++实现

下面让我们来看这 DFS的完整例子
代码如下：

#include 

// 地图大小即数据，1 表示障碍物
int map[5][5] = {
    0 ,0 ,0 ,1 ,1 ,
    0 ,0 ,0 ,1 ,1 , 
    0 ,1 ,0 ,0 ,0 ,
    0 ,0 ,0 ,1 ,1 ,
    0 ,0 ,0 ,0 ,0
};

int flag[5][5];  // 标记是否走过的路

int direction[4][2] = {
    0, 1,
    1, 0,
    0, -1,
    -1, 0
};
 
int Yes = 0;	// 用于标记是否查找到

void dfs(int x, int y);

int main()
{
    flag[0][0] = 1;  // 初始位置标记为以走过
    
    dfs(0, 0);	     // 开始搜索
    
    if(Yes)
    {
        printf("Yes, I found it !");
    }
    else
    {
        printf("No, I do not found it !");
    }
    
    return 0; 
} 

void dfs(int x, int y)
{
    if(x == 4 && y == 4)
    {
        Yes = 1;
        return;
    }
    
    int i = 0;
    for(; i < 4; i++) // 4种方向  
    {
        int nx = x + direction[i][0];  // 当前探索的方向 
        int ny = y + direction[i][1];
        
        if(nx < 0 || ny < 0 || nx > 4 || ny > 4)
   	        continue; 
        
        if(flag[nx][ny] == 0 && map[nx][ny] == 0)
        {
   	       flag[nx][ny] = 1;
   	       dfs(nx, ny);
   	       flag[nx][ny] = 0;
  	    } 
    }
}

运行程序，效果如下，发现我们已经查找了终点：

我们把地图改一下，把终点周围用障碍物围起来：

int map[5][5] = {
    0 ,0 ,0 ,1 ,1 ,
    0 ,0 ,0 ,1 ,1 , 
    0 ,1 ,0 ,0 ,0 ,
    0 ,0 ,0 ,1 ,1 ,
    0 ,0 ,0 ,1 ,0
};

如果如下：

好了，你们快去试试吧，BFS 和 DFS可以求解出很多的问题，比如人工智能贪吃蛇、连连看等等 . . .

.

---

作者：浪子花梦