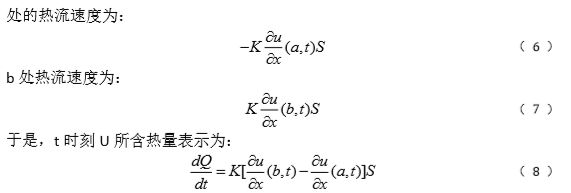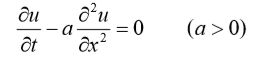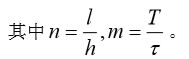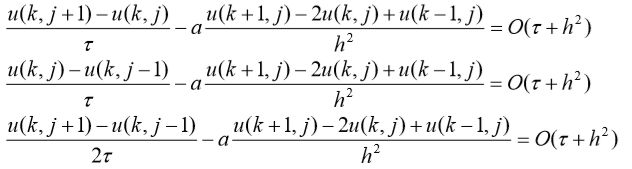2018国赛数学建模笔记

负责部分：搜集文献，推导一维热传导方程，提出解析解，第二问循环求解，论文写作

 

写作心得体会：

1、摘要很重要，基本上凭摘要初筛。必须指明研究的主要内容，使用的主要方法，得到的主要结论和成果

 

摘要

（第1段） 说一下你研究问题的背景及意义

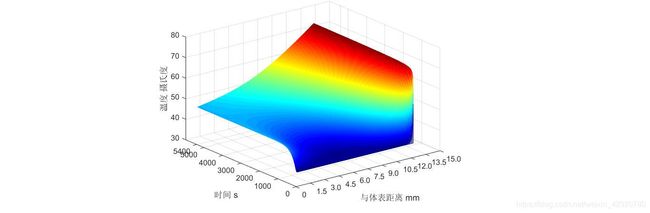
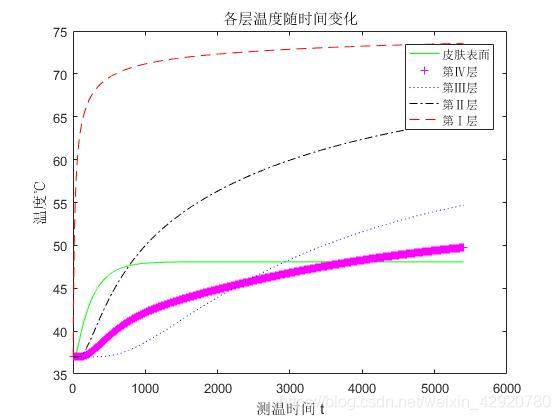
（第2段） 对于问题1我们首先建立了抛物型一维热传导模型，借助前向差分方法用MATLAB求解数值解。在考虑辐射、对流之后，可以对模型进行适当修改。

（第3段） 对于问题2我们用MATLAB进行循环迭代求最优厚度

（第4段） 对于问题3我们结合热导率公式，线性规划L2最优厚度

 

流程  

一、问题重述

二、模型假设

三、符号说明

物理背景

四、模型建立与求解

推导一维热传导方程 

偏微分方程的解析解 

偏微分方程的数值解 

模型优化

问题二、三

五、误差分析、模型检验

六、模型评价和推广

---

一、问题重述

先简要叙述一下研究问题的背景及内容，再将题目转述。

二、模型假设

1. 为使假人各部位受热相同而将假人形态近似看成圆柱体；

2. 假人体内温度恒定在 37℃ ，服装各层及皮肤表面各处的初始温度与体内温度一致，即 37℃；

3. 假设空气层为 IV 层；

4. 假设热传导传递到织物的过程中是均匀的；

5. 假设热传递为一维传递，即垂直于皮肤方向进行；

6. 假设温度传递过程中织物的材料没有发生热溶解，结构也几乎不变，即各材料的所有属性参数值保持不变（在模型优化时纳入考虑）；

7. 先假设简单模型仅存在热传导，而改进模型进一步考虑热辐射、热对流。暖体假人没有汗液系统，不考虑湿传递（水汽、汗液等影响）等；

8. 织物之间、织物与空气层之间的温度变化都是连续的，但温度梯度是跳跃的。

三、符号说明

物理背景

对于多层防护服，当织物与皮肤间空气层厚度小于或等于 6.4mm 时，由于空气层间隙太小，气体无法形成对流运动[5]，所以此问题背景下热传递方式主要有热传导与热辐射。 又由于热辐射是物体通过电磁波传递能量的，假人恒定温度为 37℃，在这个温度下所产生的电磁波传递的能量较热传导的能量非常小，可忽略不计，故本问之中热量仅通过热传导方式传递。

其他论文1    其他论文3

四、模型建立与求解

推导一维热传导方程 

  假设：（1）细杆横截面面积为常数S且很小，因此在任何时刻，都可以把横截面上的温度视作相同；

             （2）细杆侧面完全绝热，即热量只能通过两端流入或流出。 

方法一：

方法二：

Q为负，表示流出；正，流入

 

偏微分方程的解析解 

一是求解比较困难（物理数学相关知识欠缺），二是即时求出解析解为级数形式，无法确定具体数值

过程：先方程求通解，再根据初始边界条件求参数值

 

偏微分方程的数值解 

列方程

在研究热传导过程随时间变化的非定常物理问题时，常常会遇到抛物型方程。其简单的形式为一维热传导方程：

根据题意，属于初边值定解问题：

 

求解方程——偏微分方程的差分解法 

差分法（difference methods，简称DM），是一种微分方程数值方法，是通过有限差分来近似导数，从而寻求微分方程的近似解。

1、先对求解区域作网格剖分，将自变量的连续变化区域用有限离散点（网格点）集代替

2、通过用网格点上函数的差商代替导数，将含连续变量的偏微分方程定解问题化成只含有限个未知数的代数方程组。

对 xt 平面进行网格剖分，分别取 ,h 为 t方向与h方向的步长，得到一维热传导方程的不同的差分近似：

对时间分别采用向前、向后及中心差商公式， 对厚度采用二阶中心差商公式

利用前向差分法(详解）求解热传导方程的 MATLAB 程序     

%*****************************************************

function U=forwdif(f,c1,c2,a,b,c,n,m);         %定义函数

%Input - f=u(x,0) as a string 'f'

%         - c1=u(0,t) and c2=u(a,t)

%         - a and b right endpoints of [0,a] and [0,b]

%         - c the constant in the heat equation

%         - n and m number of grid points over [0,a] and [0,b]

%Output - U solution matrix;  

 

%Initialize parameters and U

h=a/(n-1);k=b/(m-1);             %横纵坐标个数

r=c^2*k/h^2;s=1-2*r;     应为c*k/h^2

U=zeros(n,m);  

 

%Boundary conditions

U(1,1:m)=c1;U(n,1:m)=c2;                  %↓↓↓↓第一秒和最后一秒在衣服各处的温度分布↓↓↓↓↓↓

 

%Generate first row

U(2:n-1,1)=feval(f,h:h:(n-2)*h)';           %第一列为u(x,0)的分布

 

%Generate remaining rows of U  

for j=2:m 
   for i=2:n-1

      U(i,j)=s*U(i,j-1)+r*(U(i-1,j-1)+U(i+1,j-1));

   end

end  

 

U=U';

%*****************************************************

利用上述函数，我们可以编写如下程序计算例 2 的数值解。

c=1;a=3;b=3;c1=0;c2=9;n=4;m=7;

f=@(x) x.^2;

sol=forwdif(f,c1,c2,a,b,c,n,m) 

 

最后利用Matlab将U可视化

服装内部温度分布图 

3、讨论差分格式解对于微分方程解的收敛性及误差估计。

模型优化

考虑：服装各材料属性参数值是随温度的升高而增大的；

          高温作业服所处的外界环境（通常为高温空气）存在热辐射和热对流，并且与皮肤相邻的空气层存在热对流。(但厚度<8mm时可忽略)                         

假设：能量转移从火焰到外壳时，包含热对流和热辐射辐射。由于外壳阻挡了大部分的辐射，因此在织物层传递过程中，可以忽略辐射；

列式：

参考文献[1][2]：在无限小的织物单元上的能量平衡产生微分方程

显热容=比热*密度

参考文献[1]

 

参考文献[1][2]

参考文献[2]

参考文献[3]

最后将方程差分，得到： 

参考文献[4]

问题二、三

 

五、误差分析、模型检验

• 前向误差分析

补充知识

 

• 
• 模型未考虑湿度和温度对材料的属性参数的影响，这就会导致 热传导率/导热系数 与实际产生误差

各种物质的热导率数值主要靠实验测定，其理论估算是近代物理和物理化学中一个活跃的课题。热导率一般与压力关系不大，但受温度的影响很大。纯金属和大多数液体的热导率随温度的升高而降低，但水例外；非金属和气体的热导率随温度的升高而增大。传热计算时通常取用物料平均温度下的数值。此外，固态物料的热导率还与它的含湿量、结构和孔隙度有关。一般含湿量大的物料热导率大。 

六、模型评价和推广

 

[1] Fan, J., Luo, Z., & Li, Y. . Heat and moisture transfer with sorption and condensation in porous clothing assemblies and numerical simulation. International Journal of Heat and Mass Transfer, 2000,43(16), 2989–3000.

[2] Trorvl D A.Heat Transfer in Thin Fibrous Materials Under High Heat Flux Conditions[D] Edmonton：University
of Alberta,1997:1—134

[3] Ahmed Ghazy.Numerical simulation of heat transfer in firefighters’ protective clothing with multiple air gaps during flash fire exposure[J]．Numerical Heat Transfer，2012，61(8):569—593

[4] 卢琳珍.多层热防护服装的热传递模型及参数最优决定[D].浙江理工大学, 2017.

[5] 潘斌.热防护服装热传递数学建模及参数决定反问题[D].浙江:浙江理工大学,2016.