你还在为排序而苦恼吗?最全的排序来喽
简言:
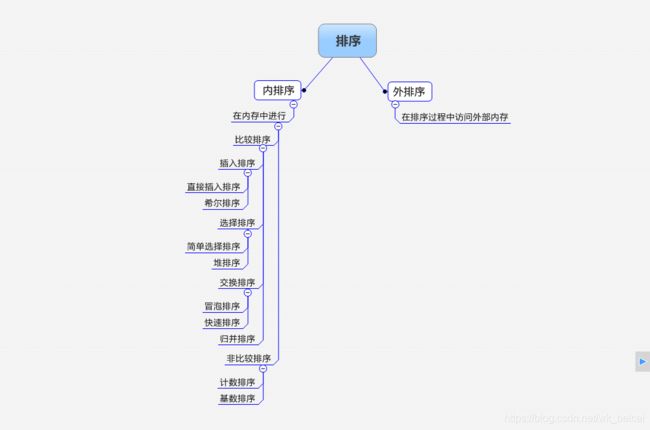
排序算法可以分为内部排序和外部排序。
内部排序是数据记录在内存中进行排序。
外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。
2. 各种排序的稳定性:
稳定性的排序有:冒泡排序,插入排序,归并排序,基数排序。
不稳定的排序有:选择排序,快速排序,希尔排序,堆排序。
1) 冒泡排序
代码展示:
public static void main(java.lang.String[] args) {
//定义一个数组
int[] arr = {12,24,34,1,43,6,8,15};
/**
* 通过循环的方式 俩俩比较
* */
for (int i = 1; i < arr.length; i++) {
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
String result = "";
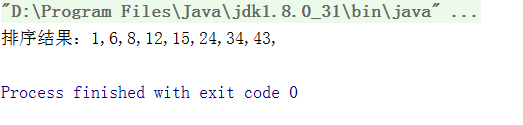
for(int i = 0;i运行结果:
冒泡排序思想:
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
2)选择排序
代码展示:
public static void main(java.lang.String[] args) {
//定义一个数组
int[] arr = {12,24,34,1,43,6,8,15};
// 总共要经过 N-1 轮比较
for (int i = 0; i < arr.length - 1; i++) {
//定义一个最小值
int min = i;
// 每轮需要比较的次数 N-i
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
// 将找到的最小值复制给定义的最小值
min = j;
}
}
// 将找到的最小值和i位置所在的值进行交换
if (i != min) {
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
String result = "";
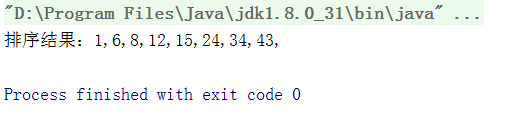
for(int i = 0;i运行结果:
选择排序思想:
在为排序中找到最小的元素,存放到排序序列的最初位置,在从生育为排序中找到最小的元素,重复第二步,知道所有元素排序完毕。
3) 插入排序
代码展示:
public static void main(java.lang.String[] args) {
//定义一个数组
int[] arr = {12,24,34,1,43,6,8,15};
// 从下标为1的元素开始选择合适的位置插入
for (int i = 1; i < arr.length; i++) {
// 记录要插入的数据
int tmp = arr[i];
// 从已经排序的序列最右边的开始比较,找到比其小的数
int j = i;
while (j > 0 && tmp < arr[j - 1]) {
arr[j] = arr[j - 1];
j--;
}
// 存在比其小的数,插入
if (j != i) {
arr[j] = tmp;
}
}
String result = "";
for(int i = 0;i运行结果:
插入排序思想:
从起始位置一次扫描未排序序列到末尾,将扫描到的每个元素插入有序序列的适当位置,
4) 快速排序
代码展示:
public static void main(java.lang.String[] args) {
//定义一个数组
int[] arr = {12,24,34,1,43,6,8,15};
int[] ints = quickSort(arr, 0, arr.length - 1);
String result = "";
for(int i = 0;i运行结果:
快速排序思想:
从数列中挑出一个元素,称为基准。重新排序数列,所有元素比基准值小的放在基准前面,所有元素比基准值大的摆放在基准的后边,然后递归的把小于基准值元素的子数列和大于基准值元素的子数列排序
5)堆排序
代码展示:
public static void main(java.lang.String[] args) throws Exception {
//定义一个数组
int[] arr = {12,24,34,1,43,6,8,15};
int[] sort = sort(arr);
String result = "";
for(int i = 0;i 0; i--) {
swap(arr, 0, i);
len--;
heapify(arr, 0, len);
}
return arr;
}
private static void buildMaxHeap(int[] arr, int len) {
for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
heapify(arr, i, len);
}
}
private static void heapify(int[] arr, int i, int len) {
int left = 2 * i + 1;
int right = 2 * i + 2;
int largest = i;
if (left < len && arr[left] > arr[largest]) {
largest = left;
}
if (right < len && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
swap(arr, i, largest);
heapify(arr, largest, len);
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
运行结果:
堆排序思想:
创建一个堆,把堆首和尾互换,把堆的尺寸缩小1,并调用shift_down(0),把新的数组顶端数据调整到相应位置。
重复步骤,知道堆的尺寸为1.
6.计数排序
代码展示:
public static void main(java.lang.String[] args) throws Exception {
//定义一个数组
int[] arr = {12,24,34,1,43,6,8,15};
int[] sort = sort(arr);
String result = "";
for(int i = 0;i 0) {
arr[sortedIndex++] = j;
bucket[j]--;
}
}
return arr;
}
private static int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}
运行结果:
计数排序思想:
花O(n)的时间扫描一下整个序列 A,获取最小值 min 和最大值 max
开辟一块新的空间创建新的数组 B,长度为 ( max - min + 1)
数组 B 中 index 的元素记录的值是 A 中某元素出现的次数
最后输出目标整数序列,具体的逻辑是遍历数组 B,输出相应元素以及对应的个数