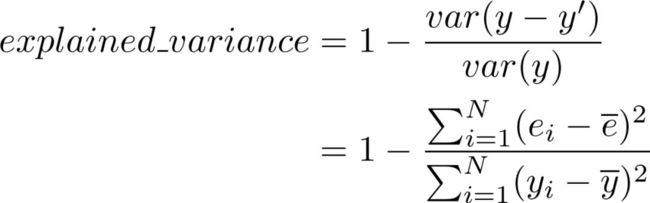机器学习基础,回归模型评估指标
![]()
文章发布于公号【数智物语】 (ID:decision_engine),关注公号不错过每一篇干货。
来源 | CrossHands
作者 | AhongPlus
回归模型中常用的评估指标可以分如下几类:
1. MAE系列,即由Mean Absolute Error衍生得到的指标;
2. MSE系列,即由Mean Squared Error衍生得到的指标;
3. R²系列;
注:在英语中,error和deviation的含义是一样的,所以Mean Absolute Error也可以叫做Mean Absolute Deviation(MAD),其他指标同理可得;
01
MAE系列
MAE 全称 Mean Absolute Error (平均绝对误差)。
更多参考:https://en.wikipedia.org/wiki/Mean_absolute_error
设N为样本数量, 为实际值,
为实际值, 为预测值,那么 MAE 的定义如下
为预测值,那么 MAE 的定义如下
由 MAE 衍生可以得到:
Mean Absolute Pencentage Error (MAPE,平均绝对百分比误差),相当于加权版的 MAE。
MAPE 可以看做是 MAE 和 MPE (Mean Percentage Error) 综合而成的指标 。
。
从 MAPE 公式中可以看出有个明显的 bug——当实际值 为 0 时就会得到无穷大值(实际值
为 0 时就会得到无穷大值(实际值 的绝对值<1也会过度放大误差)。为了避免这个 bug,MAPE一般用于实际值不会为 0 的情形。
的绝对值<1也会过度放大误差)。为了避免这个 bug,MAPE一般用于实际值不会为 0 的情形。
Sungil Kima & Heeyoung Kim(2016) 提出 MAAPE(mean arctangent absolute percentage error) 方法,在保持 MAPE 的算法思想下克服了上面那个 bug
更多参考 A new metric of absolute percentage error for intermittent demand forecasts,Sungil Kima & Heeyoung Kim, 2016。
考虑Absolute Error  可能存在 Outlier 的情况,此时 Median Abosulte Error (MedAE, 中位数绝对误差)可能是更好的选择。
可能存在 Outlier 的情况,此时 Median Abosulte Error (MedAE, 中位数绝对误差)可能是更好的选择。
02
MSE系列
MSE全称Mean Squared Error(均方误差),也可以称为Mean Squared Deviation (MSD).
更多参考:https://en.wikipedia.org/wiki/Mean_squared_error
由MSE可以衍生得到均方根误差(Root Mean Square Error, RMSE, 或者RMSD)
更多参考:https://en.wikipedia.org/wiki/Root-mean-square_deviation
RMSE可以进行归一化(除以全距或者均值)从而得到归一化的均方根误差(Normalized Root Mean Square Error, NRMSE).
RMSE还有其他变式:
1. RMSLE(Root Mean Square Logarithmic Error)
2. RMSPE(Root Mean Square Percentage Error)
对于数值序列出现长尾分布的情况,可以选择MSLE(Mean squared logarithmic error,均方对数误差),对原有数据取对数后再进行比较(公式中+1是为了避免数值为0时出现无穷值)。
03
R²系列
R²(R squared, Coefficient of determination),中文翻译为“决定系数”或者“拟合优度”,反映的是预测值对实际值的解释程度。
注意:R²和相关系数的平方不是一回事(只在简单线性回归条件下成立)。
回归模型中,增加额外的变量会提升R²,但这种提升可能是虚假的,因此提出矫正的R²(Adjusted R²,符号表示为 或
或 )来对模型中的变量个数进行“惩罚”(
)来对模型中的变量个数进行“惩罚”( )。
)。
公式中P表示回归模型中变量(特征)的个数。
和R²计算方式很相近的另一个指标是Explained Variance Score.
更多关于R²参考 :
1. ttps://en.wikipedia.org/wiki/Coefficient_of_determination
2. https://blog.minitab.com/blog/adventures-in-statistics-2/regression-analysis-how-do-i-interpret-r-squared-and-assess-the-goodness-of-fit
3. https://www.displayr.com/8-tips-for-interpreting-r-squared/
综上,在选用评价指标时,需要考虑
1. 数据中是否有0,如果有0值就不能用MPE、MAPE之类的指标;
2. 数据的分布如何,如果是长尾分布可以选择带对数变换的指标,中位数指标比平均数指标更好;
3. 是否存在极端值,诸如MAE、MSE、RMSE之类容易受到极端值影响的指标就不要选用;
4. 得到的指标是否依赖于量纲(即绝对度量,而不是相对度量),如果指标依赖量纲那么不同模型之间可能因为量纲不同而无法比较;
更多关于指标选择可以参考A Survey of Forecast Error Measures(2013)这篇文章。
参考资料:
1. https://machinelearningmastery.com/metrics-evaluate-machine-learning-algorithms-python/
2. A Survey of Forecast Error Measures, 2013
3. http://www.damienfrancois.be/blog/files/modelperfcheatsheet.pdf
4. https://scikit-learn.org/stable/modules/model_evaluation.html
5. A new metric of absolute percentage error for intermittent demand forecasts,Sungil Kima & Heeyoung Kim, 2016
6. Accuracy in forecasting: A survey, Essam Mahmoud, 1984
![]()
![]()
星标我,每天多一点智慧
![]()