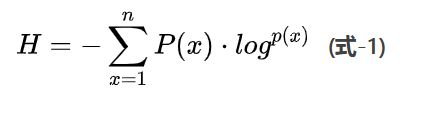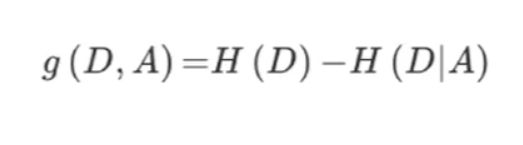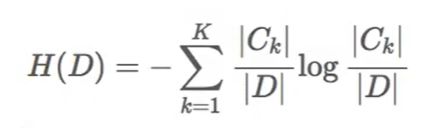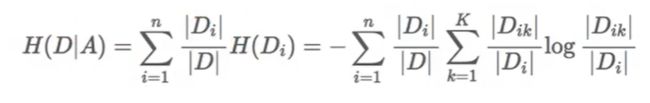信息熵-信息的数学度量，决策树的划分依据-信息增益，常见的决策树算法、优缺点，决策树算法-分类树案例

目录

1.决策树 

2.信息熵-信息的数学度量

3.决策树的划分依据-信息增益

4.常见的决策树算法

5.决策树算法-分类树

6.决策树优缺点、改进方式

参考文章

---

 

1.决策树 

　简而言之，决策树是一棵树，其中每个分支节点代表多个备选方案之间的选择，每个叶节点代表一个决策。它是一种监督学习算法，主要用于分类问题，适用于分类和连续输入和输出变量。 是归纳推理的最广泛使用和实用的方法之一（归纳推理是从具体例子中得出一般结论的过程）。决策树从给定的例子中学习和训练数据，并预测不可见的情况。

程序设计中的条件分支结构（if-then）就是决策树思想的体现，最终的决策树就是利用这类结构分隔数据的一种学习分类方法。

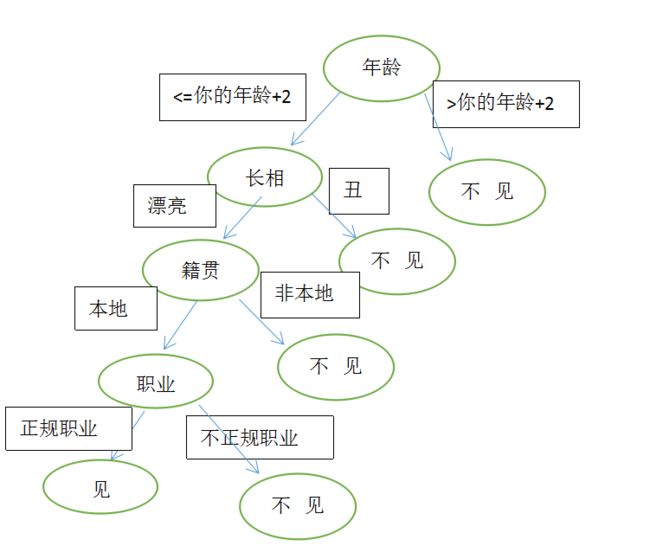
比如：媒婆给你介绍女朋友，你们的对话如下：

你：多大年纪？

媒婆：26

你：漂亮吗？

媒婆：漂亮

你：哪人呢？

媒婆：本地人

你：做的工作正规吗？

媒婆：正规工作

这一系列问答就构成了决策树，并且有一定的优先顺序，如下：

 

 

2.信息熵-信息的数学度量

在了解信息熵之前，先看下面这个例子：

假设有32只球队争夺世界杯，要求猜测冠军是哪只球队，最少需要猜几次可以得出正确答案？

学习过二分法的读者很容易得出结论：5次。

这个答案是如何得出呢？利用决策树思想做五次决策，如：

第一次：冠军是否在1-16号队伍中？

答：是的

第二次：冠军是否在1-8号队伍中？

答：是的

第三次：冠军是否在1-4号队伍中？

答：是的

第四次：冠军是否在1-2号队伍中？

答：是的

第五次：冠军是否是1号队伍？

答：不是

五次决策后得出结论：冠军是2号队伍

那么对于2^n只队伍（n取整数，n>=1），需要做决策的次数是以2为底，2的对数：log2^(2^n)=n

 

信息熵

对需要交流的人类而言，通讯犹如吃饭睡觉一样重要。就像人类不断探索水稻增产一样，不断改进通讯质量与速度的科学研究一直是全世界方兴未艾的事业。1948年，博士毕业后就在贝尔实验室里研究通讯技术的电子工程师克劳德 • 香农（Claude Shannon, 1916-2001）在《贝尔系统技术杂志》（Bell System Technology Journal）上分两期发表了他一生中也许是最有名的一篇论文：《通讯的数学理论》（A mathematical theory of communications,1948），引入了一条全新的思路，震撼了整个科学技术界，开启了现代信息论研究的先河。在这一伟大的贡献中，他引进的“信息熵”之一般概念举足轻重：它在数学上量化了通讯过程中“信息漏失”的统计本质，具有划时代的意义

 

香农最初并没有借用“熵”这个词汇来表达他关于信息传输中的“不确定性”的度量化。他甚至都不太知晓他所考虑的量与古典热力学熵之间的类似性。他想把它称为“information（信息）”，但又认为这个名词太过大众化，已被普通老百姓的日常话语用滥了。他又考虑过就用单词“uncertainty（不确定性）”，但它却更像抽象名词，缺乏量化的余地，确实难于定夺。终于有一天，他遇见了天才的数学家冯 • 诺依曼（John von Neumann, 1903-1957）。真是找对了人！冯·诺依曼马上告诉他：

就叫它熵吧，这有两个好理由。一是你的不确定性函数已在统计物理中用到过，在那里它就叫熵。第二个理由更重要：没人真正理解熵为何物，这就让你在任何时候都可能进能退，立于不败之地。

 

香农的信息熵本质上是对我们司空见惯的“不确定现象”的数学化度量。譬如说，如果天气预报说“今天中午下雨的可能性是百分之九十”，我们就会不约而同想到出门带伞；如果预报说“有百分之五十的可能性下雨”，我们就会犹豫是否带伞，因为雨伞无用时确是累赘之物。显然，第一则天气预报中，下雨这件事的不确定性程度较小，而第二则关于下雨的不确定度就大多了。

 

球队夺冠不确定性分析

（1）

根据香农对于信息熵的定义可知，假如32只球队每只球队的夺冠概率相同，设n为球队总数，1/n为任意一只球队夺冠的概率，则有1/n=1/32

如果我们用符号 H(1/n，1/n，...1/n) 来表示一个样本空间的不确定度，根据香农提供的公式，有：

H=-(1/nlog1/n+1/nlog1/n+1/nlog1/n..+1/nlog1/n)

（关于公式的推导可参考文章最下方的链接）

所以32只球队在每只球队夺冠概率相同的情况下，则(这里的log以2为底,下面为演示省略2）：

H=-(1/32*log1/32+1/32*log1/32+1/32*log1/32..+1/32*log1/32)

=-(1/32*log2^(-5)+1/32*log22^(-5)+1/32*log2^(-5)+..+1/32*log2^(-5))

=-（1/32 * (-5) * 32）=5 bit

（此处不可省略负号，因为概率是小于1的，对概率求log自然也小于1，需取负号进行补正）

（2）

计算出信息熵的大小后，香农进一步提出：

当一个样本里的所有事件等概率的情况下，此时的信息熵为最大值，设n为球队标号，设pn为标号为n的球队夺冠概率，则有：

H(p1,p2,p3...pn) <= H(1/n,1/n,1/n...1/n)

谁是世界杯冠军的信息量应该比5bit少，根据香农的研究，它的准确信息量应该是

H=-(p1logp1+p2logp2+...p32logp32)

H即信息熵，单位为bit

公式为：

（3）

当这32只球队夺冠概率相同时，对应的信息熵为5bit

但是在实际生活中，每只球队的夺冠概率是不同的，强队的夺冠概率大于弱队，如德国队，巴西队，葡萄牙这些夺冠热门。

假设德国队得冠概率为1/4，巴西队夺冠概率为1/4，葡萄牙夺冠概率1/8，中国队夺冠概率1/32，其余队伍夺冠概率为pn，那么就有

H=-(1/4log1/4+1/4log1/4+1/8log1/8+1/32log1/32+.....+pnlogpn)<5bit

 

结论：

当得到一个确定信息后，信息熵就减小了，所以信息和消除不确定性是相联系的。信息熵越大，不确定性就越强，信息熵越小，确定性就越强，已知信息也就越多。

始终记住一句话：信息熵是描述信息的数学符号，当信息熵的大小越大时，不确定性就越强。当信息熵为0，不确定性就被完全消除了，此时的信息就是绝对可信的。

 

3.决策树的划分依据-信息增益

什么是信息增益

当得知一个特征条件之后减少的信息熵的大小

计算公式

D为信息集合，H(D)为D信息下未增益前的信息熵大小，H(D|A)为给定条件A下的D的信息条件熵。g(D,A)为特征A对训练数据集D的信息增益，定义为集合D的信息熵H(D)与特征A给定条件下的D的信息条件熵H（D|A）之差，公式为:

信息熵H(D)计算公式，D为总样本数，Ck为类别为i的样本数：

 

条件熵H(D|A)公式，D为总样本数，Di为在某个特征条件下条件为i的样本数，Dik为在Di的条件下类别为k的样本数。

补充：需要注意的是，若未标明底数的情况下，大多数情况下log以2为底

 

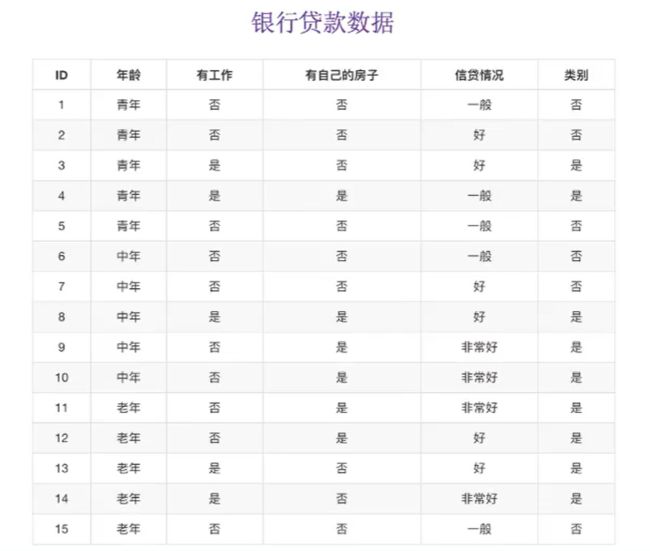
有这么一组银行贷款数据，我们需要根据每个ID的信息判断此ID是否有资格贷款。当我们得到一个样本，要判断此样本是否有贷款资格，根据信息熵的思想，我们要消除不确定性因素，当所有因素对消除不确定性重要性相等时，信息熵为最大值。

表格仅列举了部分影响因素，如年龄，有工作，有自己的房子，信贷情况。在实际情况中，不同的因素对贷款资格评估有着不同的影响性。

利用信息熵和条件熵公式，我们来求年龄的条件熵g(D|年龄)

g(D|年龄) = H(D)-H(D|年龄)

=-(9/15log9/15+6/15log6/15)  -  [5/15H(青年)+5/15H(中年)+5/15H(老年)]

=-[0.971 + 1/3[ -(2/5log2/5+3/5log3/5) - (2/5log2/5+3/5log3/5) - (4/5log4/5+1/5log1/5)]

=-(0.971 + 1/3( -0.9709 -0.9709 -0.7219))

=0.1718

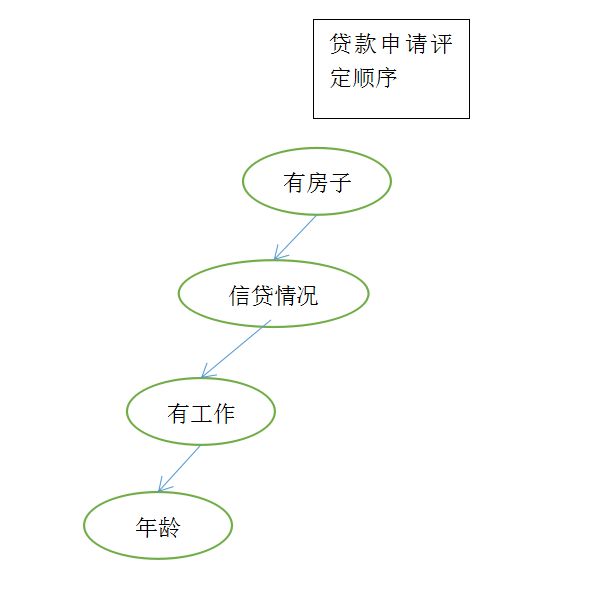
既然我们有了这两个公式，就可以根据前面的是否通过贷款申请的例子来计算出决策特征顺序

我们让A1、A2、A3、A4分别表示年龄，工作，房子，信贷情况四个特征

依次计算出的信息增益为0.1718,、0.324、0.420、0.363

相比较而言A3即有房子的信息增益最大，所以A3为最大信息增益

此时可以结合决策树思想来做划分，比如有自己的房子对评估影响性非常大（房子可做资产抵押），所以排到第一位，其次为信贷情况，有无工作，年龄

 

 

 

4.常见的决策树算法

• ID3:信息增益，最大准则
• C4.5：信息增益比，最大准则
• CART：回归树：平方误差最小    或  分类树：基尼系数，最小准则

 

5.决策树算法-分类树

泰坦尼克号人员存活情况估计

网址：http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt

部分样本如下：

"row.names","pclass","survived","name","age","embarked","home.dest","room","ticket","boat","sex"

"1","1st",1,"Allen, Miss Elisabeth Walton",29.0000,"Southampton","St Louis, MO","B-5","24160 L221","2","female"
"2","1st",0,"Allison, Miss Helen Loraine", 2.0000,"Southampton","Montreal, PQ / Chesterville, ON","C26","","","female"
"3","1st",0,"Allison, Mr Hudson Joshua Creighton",30.0000,"Southampton","Montreal, PQ / Chesterville, ON","C26","","(135)","male"
"4","1st",0,"Allison, Mrs Hudson J.C. (Bessie Waldo Daniels)",25.0000,"Southampton","Montreal, PQ / Chesterville, ON","C26","","","female"

第一行为特征信息，分别对应：行号，票类别，存活，姓名，年龄，登陆地，出发地，房间号，票，船，性别。

票类别是指1，2，3，对于高铁票如一等座，二等座，商务座。

我们抽取对存活有影响的特征，如票类别，年龄，房间号，性别

 

sklearn决策树API：sklearn.tree.DecisionTreeClassifier(criterion='',max_depth='',random_state='')

• criterion默认是gini系数，也可以选择信息增益熵entropy
• manx_depth:树的深度
• random_state:随机数种子 

上程序

import math
import pandas as pd
from  sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

def decision():
    train=pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")

    #特征为'pclass','age','room','sex'
    #目标值survived
    x=train[['pclass','age','room','sex']]
    y=train['survived']

    #age的缺失值使用平均数填补
    #房间号的缺失值用0补充（可能产生不好的情况）
    x['age'].fillna(x['age'].mean(), inplace =True)
    x['room'].fillna(0, inplace=True)

    #划分特征和目标值的测试集，训练集，比例0.25
    x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25)

    #对特征值做one-hot编码处理
    dv=DictVectorizer(sparse=False)

    #使用训练的集的预估器结果
    #对训练集和测试集做转化
    x_train=dv.fit_transform(x_train.to_dict("records"))
    x_test=dv.transform(x_test.to_dict("records"))

    print(dv.get_feature_names())
    print(x_train)

    #使用决策树算法进行测试集预测
    dec=DecisionTreeClassifier()
    #训练集学习
    dec.fit(x_train,y_train)

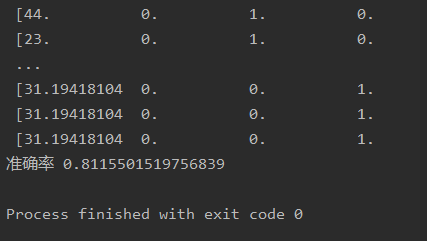
    print("准确率",dec.score(x_test,y_test))

if __name__=="__main__":
    decision()

预估准确性： 

导出决策树：

Seklearn API：sklearn.tree.export_graphviz(estimator,out_file='tree.dot',feature_name=[''])

在程序里导入export_graphviz方法，在调用决策树函数后导出

from sklearn.tree import export_graphviz
export_graphviz(dec,out_file="./tree.dot")

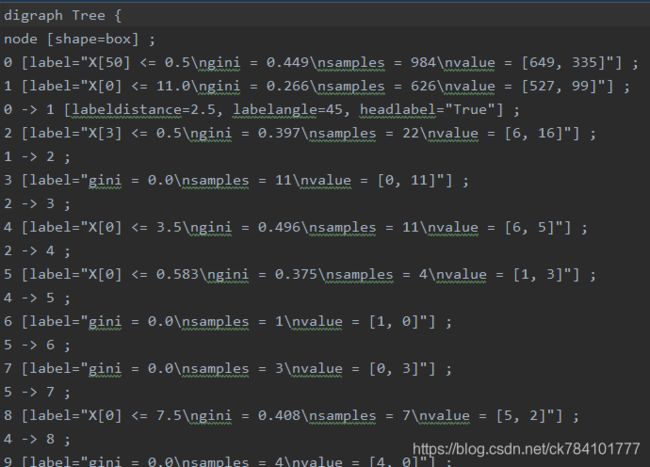
导出结果为.dot文件，如下

若想将dot文件转换为pdf或Png格式，需安装graphviz

ubuntu : apt install graphviz

centos: yum install graphviz

windows:http://www.graphviz.org/官网下载

执行命令

dot-Tpng tree.dot -o tree.png

dot-Tpdf tree.dot -o tree.pdf

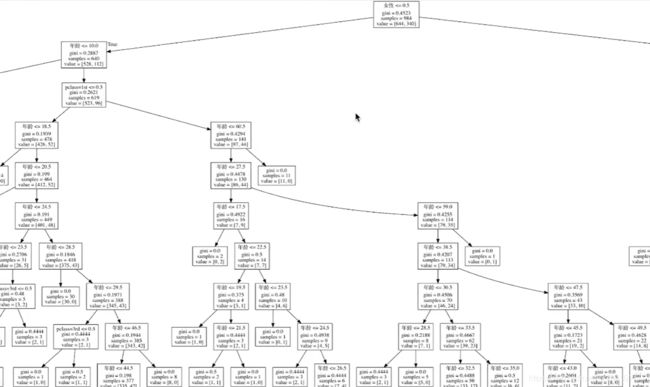
 生成形如下图的结构：

补充：

可选择基尼系数或信息增益熵作为划分标准，或调整数的深度进行优化调参，进一步提升准确率

• criterion默认是gini系数，也可以选择信息增益熵entropy
• manx_depth:树的深度

 

6.决策树优缺点、改进方式

优点

• 简单的理解和解释，树木可视化，可看到决策过程
• 需要很少的数据处理，其他技术通常需要做数据归一化或标准化

缺点

• 对于各类别样本数量不一致的数据, 信息增益偏向于那些更多数值的特征
• 容易过拟合
• 忽略属性之间的相关性

改进方式

• cart剪枝算法：CART剪枝算法从“完全生长“的决策树的底端剪去一些子树，使决策树变小（模型变简单），从而能够对未知数据有更准确的预测。
• 随机森林

 

参考文章

信息的度量——熵 https://www.jianshu.com/p/9f1bb824f912

信息熵 https://www.cnblogs.com/IamJiangXiaoKun/p/9455689.html

信息熵是什么【推荐】https://www.zhihu.com/question/22178202

基尼系数https://www.jianshu.com/p/abfec6ecf974

决策树优缺点 https://www.jianshu.com/p/655d8e555494