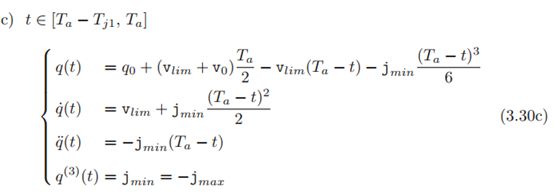分段式S形速度规划算法

1 典型七段式S形速度曲线

典型7段式S形曲线位置q、速度v、加速度a、加加速度j的波形如图所示：

位置q和时间t的关系式：

2 分段式S形曲线速度规划

已知初速度V0,末速度Ve,最大速度Vmax，路程距离s，最大加速度amax,最大jerk（加加速度）jmax,要规划位置、速度、加速度、加加速度随时间变化的曲线。具体步骤如下：

1） 假设能够达到最大速度Vmax，此时计算加速时间Ta和减速时间Td

此时需要判断最大加速度amax是否能够达到

在加速阶段，有关系式：

推导出：

由于匀加速和匀减速阶段是对称的,所以在临界情况下有：

则当 (Vmax-V0)j

当(Vmax-V0)j

此时最大加速度为 alim=j*Tj1

否则，存在匀加速阶段，匀加速度阶段加速度为amax，此时有关系式：

这里T2为匀加速阶段的时间。上式可以推导出Ta=Tj1+(Vmax-V0)/amax

同理，可以求出减速阶段的时间Tj2和Td。

加速段时间Ta和减速度时间Td都求出以后，可以求匀速段时间Tv。由对称性，加速段平均速度为(V0+Vmax)/2，减速度时间平均速度为(Ve+Vmax)/2，则有关系式：

Tv*Vmax+Ta*(v0+Vmax)/2+Td*(Ve+Vmax)/2=s

求出Tv=s/Vmax-Ta(V0/Vmax+1)/2+Td*(Ve/Vmax+1)/2

若Tv>0，则有匀速阶段，匀速度Vmax，此时可以按照第1节的公式求出7段式轨迹各段的位置、速度、加速度和加加速度。

若Tv<=0,则证明不能达到最大速度Vmax。

2） 不能达到最大速度Vmax

此时不存在匀速阶段。首先假设此时能够达到最大加速度Vmax，此时有：

其中 

这里具体delta的推导见论文《数控系统S型曲线加减速快速规划研究》。

若计算得到的Ta<2*Tj1或Td<2*Tj1，那么最大加速度amax没有达到，此时可以通过减少amax,直到满足Ta>2*Tj1或Td>2*Tj2为止。

3 Matlab实现代码

%通过直接确定轨迹参数的方法，计算并且画出双S曲线。
%定义变量 , 现在的初始值都按找书中的例子给定
q0 = 0  
q1 = 10
vmax = 10
max = 10
v0 = 0
v1 = 0
amax = 20
jmax = 30
count=0

%根据轨迹规划的流程，首先根据初始调节与限制条件判断是否存在云加速段
%首先按照能够达到最大速度vmax，来计算Ta,Tb,Tj1 Tj2, Tv
if (vmax -v0)*jmax < amax^2
    if v0>vmax
        Tj1 = 0; 
        Ta = 0;
        alima = 0;
    else
        Tj1 = ((vmax - v0)/jmax)^0.5;
        Ta = 2*Tj1;
        alima = Tj1 * jmax;
    end
else
    Tj1 = amax/jmax;
    Ta = Tj1 + (vmax-v0)/amax;
    alima = amax;
end

if (vmax -v1)*jmax < amax^2
    Tj2 = ((vmax - v1)/jmax)^0.5;
    Td = 2*Tj1;
    alimd = Tj2* jmax;
else
    Tj2 = amax/jmax;
    Td = Tj2 + (vmax-v1)/amax;
    alimd = amax;
end
    
Tv = (q1 - q0)/vmax - Ta/2*(1+v0/vmax) - Td/2*(1+v1/vmax)
T = Tv + Ta + Td
%Tv>0 说明可以达到最大速度，进入计算轨迹，并画图
p  = [];
vc = [];
ac = [];
jc = [];
if Tv > 0
    vlim = vmax;
    T = Tv + Ta + Td
else
    Tv = 0;
    %说明没有办法达到最大速度，判断是否能够达到最大加速度
    %首先重新计算Ta,Tb
    amax_org = amax;
    delta = (amax^4)/(jmax^2) + 2*(v0^2+v1^2) + amax*(4*(q1 - q0) - 2*amax/jmax*(v0+v1));
    Tj1 = amax/jmax
    Ta = (amax^2/jmax - 2*v0 + delta^0.5)/2/amax
    Tj2 = amax/jmax
    Td = (amax^2/jmax - 2*v1 + delta^0.5)/2/amax
    vlim = v0 + (Ta - Tj1)*alima
    while Ta < 2*Tj1||Td < 2*Tj2
        count = count+1;
        amax = amax - amax_org*0.1;
        alima = amax;
        alimd = amax;
        if amax>0
            delta = (amax^4)/(jmax^2) + 2*(v0^2+v1^2) + amax*(4*(q1 - q0) - 2*amax/jmax*(v0+v1));
        else
            delta = (amax^4)/(jmax^2) + 2*(v0^2+v1^2) - amax*(4*(q1 - q0) - 2*amax/jmax*(v0+v1));
        end
        Tj1 = amax/jmax;
        Ta = (amax^2/jmax - 2*v0 + delta^0.5)/2/amax;
        Tj2 = amax/jmax;
        Td = (amax^2/jmax - 2*v1 + delta^0.5)/2/amax;
        vlim = v0 + (Ta - Tj1)*alima;
        vlima = vlim;
        vlimb = v1 - (Td - Tj2)*alimd;
    end
    disp('这里打印出计算出来的Ta,Tb,')
    Tj1
    Ta
    Td
    amax
    if Ta <0||Td<0
        if v0>v1
            %这里只需要一个减速段
            Ta =0;
            Tj1 = 0;
            alima = 0;
            Td = 2*(q1 - q0)/(v1 + v0);
            Tj2 = (jmax*(q1 - q0) - (jmax*(jmax*(q1 - q0)^2 + (v1 + v0)^2*(v1 - v0)))^0.5)/jmax/(v1 + v0);
            alimd = -jmax*Tj2
            vlim = v1 - (Td - Tj2)*alimd
            alimd = -alimd
        else
            Td =0;
            Tj2 = 0;
        
            Ta = 2*(q1 - q0)/(v1 + v0);
            Tj1 = (jmax*(q1 - q0) - (jmax*(jmax*(q1 - q0)^2 - (v1 + v0)^2*(v1 - v0)))^0.5)/jmax/(v1 + v0);
            alima = jmax*Tj1;
            vlim = v0 + (Ta - Tj1)*alima
        end
    end

%     amax = amax_org;
%     while Td < 2*Tj2
%         amax = amax - amax_org*0.1;
%         alimb = amax;
%         Tj2 = amax/jmax;
%         Td = (amax^2/jmax - 2*v1 + delta^0.5)/2/amax;     
%     end
    
%     if Td <0
%         Td =0;
%         Tj2 = 0;
%         
%         Ta = 2*(q1 - q0)/(v1 + v0);
%         Tj1 = (jmax*(q1 - q0) - (jmax*(jmax*(q1 - q0)^2 - (v1 + v0)^2*(v1 - v0)^0.5)))/jmax/(v1 + v0);
%         alima = jmax*Tj1;
%         vlim = v0 + (Ta - Tj1)*alima
%     end
    Tj1
    Tj2
    Ta
    Td
    alima
    alimd
    T = Tv + Ta + Td
%     vlim = v0 + alima * Tj1^2 + (Ta - 2*Tj1)*alima
     
end
for t = 0:0.001:T
%         加速段轨迹
        if t>=0&&t= Tj1&&t<(Ta - Tj1)
            q = q0 + v0*t + alima/6*(3*t^2 - 3*Tj1*t + Tj1^2);
            p = [p q];
            v = v0 + alima*(t - Tj1/2);
            vc = [vc v];
            a = alima;
            ac = [ac a];
            jc = [jc 0];
        elseif t>=(Ta - Tj1)&&t < Ta
            q = q0 + (vlim + v0)*Ta/2 - vlim*(Ta - t) + jmax*(Ta - t)^3/6;
            p = [p q];
            v = vlim - jmax*(Ta - t)^2/2;
            vc = [vc v];
            a = jmax*(Ta - t);
            ac = [ac a];
            jc = [jc -jmax];
         %匀速段   
        elseif t>=Ta&&t<(Ta + Tv)
            q = q0 + (vlim + v0)*Ta/2 + vlim*(t - Ta);
            p = [p q];
            v = vlim;
            vc = [vc v];
            a = 0;
            ac = [ac 0];
            jc = [jc 0];           
        %减速段    
        elseif t>=(T - Td)&&t <(T - Td + Tj2)
            q = q1 - (vlim + v1)*Td/2 + vlim*(t - T + Td) - jmax*(t - T + Td)^3/6;
            p = [p q];
            v = vlim - jmax*(t - T + Td)^2/2;
            vc = [vc v];
            a = -jmax*(t - T + Td);
            ac = [ac a];
            jc = [jc -jmax];
        elseif t>=(T - Td + Tj2)&&t<(T - Tj2)
            q = q1 - (vlim + v1)*Td/2 + vlim*(t - T + Td) - alimd/6*(3*(t - T + Td)^2 -3*Tj2*(t - T + Td) + Tj2^2);
            p = [p q];
            v = vlim - alimd*(t - T + Td - Tj2/2);
            vc = [vc v];
            a = -alimd;
            ac = [ac a];
            jc = [jc 0];
        elseif t>=(T - Tj2)&& t

当q0 = 0, q1 = 10, v0 = 1, v1 = 0,vmax = 5, amax = 10, jmax = 30时，为典型的7段式S曲线，

当q0 = 0, q1 = 10, v0 = 1, v1 = 0,vmax = 10, amax = 10, jmax = 30时，为5段式S曲线：

当q0 = 0, q1 = 10, v0 = 7, v1 = 0,vmax = 10, amax = 10, jmax = 30时，为4段式S曲线：

当q0 = 0, q1 = 10, v0 = 7.5, v1 = 0,vmax = 10, amax = 10, jmax = 30时，为3段式S曲线：