【附原版word下载】数据结构《家族关系查询系统》课程设计
原版Word下载:下载链接
| 一、设计目的、内容及要求 1、设计目的 ⑴根据实际问题的具体情况,结合数据结构与算法课程中的基本理论和基本算法,正确分析出数据的逻辑结构,合理的选择相应的存储结构,并能设计出解决问题的有效算法。 ⑵提高程序设计和调试能力。测试员通过上机实习,验证自己设计的算法的正确性。学会有效利用基本调试方法,迅速找出程序代码中的错误并且修改。 ⑶培养算法分析能力。分析所设计的算法与数据结构描述,深刻理解程序中的代码含义,进一步提高程序设计水平。 2、设计内容及要求 ⑴分析问题,完成本题目要求的基本功能,程序能正确运行,无明显错误,为解决问题设计算法。 ⑵分析问题的特点,介绍算法说明部分,给出主要模块的算法描述。通过规范的程序流程图或伪代码描述,来体现各算法本身的逻辑结构。 ⑶经过上机调试,源程序运行正确,并且实现算法要求的功能,解决课程设计题目中给出的问题后,分析探讨测试结果。进一步体会:程序=数据结构+算法 |
| 二、预期的设计成果
1、使用C++编程语言实现家族关系查询系统的各项功能,并添加适当注释; 2、撰写课程设计实验报告一份,包括封皮、任务书、正文(任务分配、简介、算法说明、测试结果、分析与探讨)、附录(源代码)等。 |
| 三、进程安排
12月11日上午:查阅资料,确定分组、扮演角色和选题; 12月13日—18日:根据不同的角色,展开讨论,分工完成自己负责的任务; 12月20日:答辩验收。 |
目录
一、任务分配
二、简介
(一)课程设计项目背景
(二)程序具有的功能:
三、算法说明
(一)数据结构的定义
(二)总体设计
1.建立家族关系函数:
2.打开家族关系函数:
3.建立家族关系树函数:
4.添加新成员函数:
5.查找成员是否存在函数:
6.查找成员祖先函数:
8.确定成员是第几代函数:
9.查找成员双亲函数:
10.查找成员兄弟函数:
11.查找成员的子孙后代函数:
12.查找成员堂兄弟函数:
13.查找一个成员的所有孩子函数:
14.主函数:统筹调用各个函数实现相应功能
四、测试结果
(一)测试用例
1、新建一个家族关系
2、打开一个家族关系
3、添加新成员的信息
4、查找一个成员的祖先
5、查找一个成员的祖先路径
6、确定一个成员是第几代
7、查找一个成员的双亲
8、查找一个成员的兄弟
9、查找一个成员的堂兄弟
10、查找一个成员的孩子
11、查找一个成员的子孙后代
12、退出系统
(二)执行错误
(三)逻辑错误
1、open()方法错误
2、检测方法参数的必要性以及正确性
3、append()添加失败
4、append()添加成员#消失
五、分析与探讨
附录 主要源代码
原版Word下载
一、任务分配
·程序员:***。主要任务:负责算法的设计,并完成源代码的编写。
·测试员:***。主要任务:负责设计测试用程序,并对实验结果进行整理分析,最后完成实验报告的第四、第五部分内容,即测试结果与分析探讨部分。
·文档员:***。主要任务:负责撰写实验报告的第一、第二、第三部分内容,即实验内容简介与算法描述。同时完成整个文档的整合,使整篇报告排版、文字风格统一。
二、简介
(一)课程设计项目背景
家谱是一种以表谱形式,记载一个以血缘关系为主体的家族世系繁衍和重要人物事迹的特殊图书载体。家谱是中国特有的文化遗产,是中华民族的三大文献之一,属珍贵的人文资料,对于历史学,民族学,人口学和经济学的深入研究,均有不可替代的重要功能,本项目对家谱管理进行简单的模拟。
设计功能能够将信息存入文件中,以便下次访问,能够对当前家族添加新成员,实现动态查询。在家族关系查询中包括了许多查询功能,可通过输入不同的命令和参数有选择的实现各种查询。编写程序时,创造性的加入了修改成员信息功能,并能及时更新保存。
(二)程序具有的功能:
- 新建一个家族关系并建立文本文件。
- 建立家族关系树。
- 打开一个家族关系。
- 添加新成员信息。
- 查找一个成员是否存在。
- 查找一个成员的祖先。
- 查找一个成员的祖先路径。
- 确定一个成员是第几代。
- 查找一个成员的双亲。
- 查找一个成员的兄弟。
- 查找一个成员的堂兄弟。
- 查找一个成员的孩子。
- 查找一个成员的子孙后代。
- 删除一个成员。
三、算法说明
(一)数据结构的定义
因为家族的成员之间存在一个对多个的层次结构,所以不能用线性表来表示和实现。家谱从形式上看像一颗倒长的树,所以用树形结构来表示比较合适。
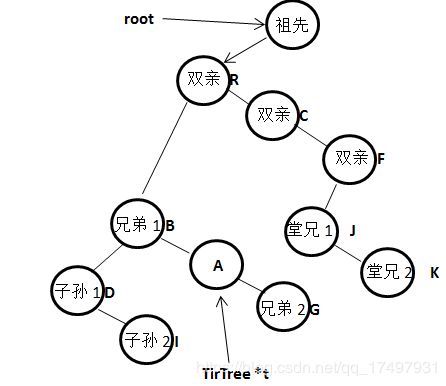
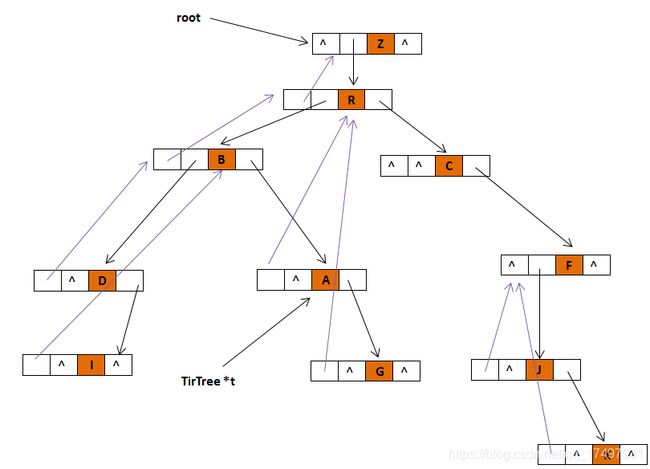
本实验采用树状结构,队列以及文件操作。将家族关系信息转化为二叉树信息,树型结构采用三叉链来实现,队列采用链式队列实现。直观看来树是以分支关系定义的层次结构,为了能够用二叉树表示祖先、孩子、兄弟三种关系,特采用图1以下存储关系(左孩子右兄弟表示法),则能在二叉树上实现家谱的各种运算。
全局变量定义:
DataType fname[MAXNUM],family[50][MAXNUM];宏定义:
#define MAXNUM 20
typedef char DataType;树的三叉链表存储结构定义为: //利用队列的存储结构来辅助创建三叉链表
| parent |
lchild |
data |
rchild |
typedef struct TriTNode //用结构体存储每一个家族成员的基本信息
{
DtatType data[MAXNUM];
struct TriTNode *parent; //用结构体存储双亲结点
struct TriTnode *lchild; //用结构体存储左孩子结点
struct TriTNode *rchild; //用结构体存储右孩子结点
}TriTree;
队列的结点结构:
typedef struct Node //用结构体存储表示队列结点
{
TriTree *info;
struct Node *next;
}Node;
链接队列类型定义: //队列采用链式队列实现
typedef struct
{
struct Node *front; //头指针
struct Node *rear; //尾指针
}LinkQueue;
(二)总体设计
实验由主函数、建立家族关系函数、建立家族关系树函数、打开家族关系函数、查找成员是否存在函数、添加新成员函数、查找成员祖先函数、查找成员祖先路径函数、查找成员为第几代函数、查找成员双亲函数、查找成员兄弟函数、查找成员堂兄弟函数、查找成员所有孩子函数和查找成员子孙后代函数14个函数共同组成。其功能描述如下:
1.建立家族关系函数:
TriTree *Create(DataType familyname[MAXNUM])输入形式:
输入时每个结点信息占一行,一个结点有多个兄弟时,以“@”作为兄弟结点结束标志,结点若无孩子,直接以“@”代替,最后以“#”作为结束标志。
图1 家族关系树
图1所示的家族关系,输入的结点信息的序列为:
祖’\n’@’\n’父’\n’父’\n’父’\n’@’\n’子’\n’@’\n’子1’\n’子2’\n’@’\n’@’\n’孙1’\n’孙2’\n’@’\n’#2.打开家族关系函数:
TriTree *Open(DataType familyname[MAXNUM])基本思想:
①输入家族关系名,以家族关系名为文件名打开文件。
②如果家族关系不存在,返回空;如果存在,打开文件,读取文件。
③将文件中的每行信息一次存储在数组family[]中。
3.建立家族关系树函数:
TriTree *TriTreeCreate()基本思想:
采用指针数组作为队列,保存输入的结点地址。指针root永远指向队头结点,即双亲结点。队列的尾指针指向当前结点,头指针指向当前结点的双亲节点。输入的结点信息已经存储在字符数组family中。
实现步骤:
①将信息复制到字符串数组ch中,如果ch不是“@”,则建立一个新结点。
②若新结点是第一个结点,则它是根结点,将其入队,指针tree指向这个根结点。
③如果不是根结点,则将当前结点链接到双亲结点上,即当前结点的双亲指针就是队头元素,然后将当前结点入队列。
④判断flag的值,如果flag=0,表明当前结点没有左孩子,那么当前结点就是双亲结点的左孩子。否则,当前结点就是双亲的右孩子。
⑤用指针root指向刚刚入队的结点。
⑥继续复制数组family的下一个元素。
⑦如果ch是“@”,则flag=0(因为“@”后面的第一个孩子为左孩子),同时判断“@”是否为第一次出现,如果是第一次,则令标志start=1;如果不是第一次出现,则出队列,root指向队头元素(实际上root总是指向双亲结点)。
⑧继续执行⑥及以下,直到遇到“#”结束。函数返回跟指针tree。
4.添加新成员函数:
Void Append(TriTree *t)
添加新成员要根据其双亲确定其在家族中的位置;以写入方式打开文件。
程序流程图:
图2 添加新成员
添加的新成员要根据其双亲确定其在家族中的位置。首先判断该双亲是否在此家族关系中,若存在,则查找其双亲,将新结点插入其双亲的最后一个孩子之后;若没有孩子,则直接作为左孩子插入。以写入的方式打开文件,如果文件打开,则更新family数组中信息,并查找新成员的双亲所在位置和与其对应的“@”个数,如果“@”个数小于双亲位置,则添加“@”使之相等,新成员插入到最后“@”之前。最后将family数组中信息写入文件保存,关闭文件。
5.查找成员是否存在函数:
TriTree * Search(TriTree *t,DataType str[])用递归算法实现。如果树空,返回NULL。如果根结点就是要查找的成员,返回根结点;否则,队规查找它的左右子树。
TriTree * Search(TriTree *t,DataType str[])函数相关描述:
如果树空,则返回NULL,如果找到,则返回该成员指针;如果没找到,遍历左右子树进行递归查找,结点不为空就查找。
6.查找成员祖先函数:
Void Ancesstor(TriTree * t)基本思想:
①判断输入的姓名是否在该家族中存在;
②若存在,则返回该家族的根结点信息。
伪代码:
Void AncesstorPath(TriTree *t)
{
If(结点t==根节点)
Printf(”%s无祖先!”)
Else
While(1){
T指针访问当前成员祖先;
Printf(祖先信息);
If(t指针==NULL)
break;
}
}
7.查找成员所有祖先路径函数:
Void AncesstorPath(TriTree *t)查找一个成员的所有祖先路径,需要从他的双亲一直向上找到根结点。
程序流程图:
图3 查找成员所有祖先路径
函数描述:
对于结点t,先判断它是否是根结点(根结点的双亲为NULL),如果是根结点,直接输出它本身;如果不是,查找它的双亲指针指向的结点,将双亲输出。继续查找,直到找到根结点。
8.确定成员是第几代函数:
Void Generation(TriTree *t)该成员到根结点之间的祖先个数即可以确定该成员为第几代。
基本思想:
①从结点t开始一直向上查找到根结点。
②查找过程中用变量count(初值=1)计数,最后输出count。
程序流程图:
图4 确定一个成员是第几代
函数描述:
确定一个成员是第几代,只要知道从它本身到根结点包括的祖先个数就可以。因而对于结点t,从本身开始一直向上查找到根结点,查找的过程中用变量count(初值为1)计数,最后输出count。
9.查找成员双亲函数:
Void Parent(TriTree *t)基本思想:
①先判断结点t是否是根结点,若不是根结点,直接输出该结点双亲指针指向结点信息;
②若是根结点,输出提示信息,结点无双亲。
伪代码:
Void Parent(TriTree *t)
{
If (t!==根结点)
Printf 双亲->结点信息; //该节点双亲指针指向的结点信息
Else
Printf (”%s无双亲!”);
}
10.查找成员兄弟函数:
Void Brothers(TriTree *t,DataType str[])成员的兄弟为其双亲除了该成员以外的所有孩子。
数据结构关系图:
图5 成员A树状结构图
图6 成员A树状结构图
结合图5和图6分析查找一个成员兄弟函数的基本思想:
输入成员t和家族关系树,假设图6为用户输入的家族关系树,待查找的成员是结点A。由图5可得关于成员A的家族关系树状结构图。即在内存中的实际存储形式(左孩子右兄弟表示法)。
图5和图6便于理解和讨论查找成员A的兄弟的过程而设置。由图5显然可知成员A的兄弟结点:兄弟1 B和兄弟2 G。图6为关于图5数据结构的详细表示图,即树状结构采用三叉链表实现。
结合图6,对于结点t,先判断他是否为根结点(t->parent==NULL)?若是根结点,则无兄弟;否则,将对结点t的双亲结点R操作(t=t->parent)。
判断双亲R的左孩子(t=t->lchild)和左孩子的兄弟(t=t->lchild->rchild)是否都存在?若只有左孩子,则左孩子就是待查找的成员A,不算。如果都不存在,则无兄弟。如果都存在,即如图6的兄弟1 B结点和兄弟2 G结点,对结点B操作(t=t->lchild)。
如果结点B不是结点A,则将结点B输出。
接着查找结点A(t=t->rchild),判断结点A是否是结点A,若不是,则将结点信息输出,继续查找结点G(t=t->rchild),以此类推直到NULL为止。
11.查找成员的子孙后代函数:
Void InOrder(TriTree *t) //中序遍历函数
void Descendants(TriTree *t) //查找一个成员的子孙后代函数一个成员的子孙后代就是其左子树上的所有结点,所以对其左子树进行中序遍历即可。
Void InOrder(TriTree *t)函数的思想:
如果二叉树存在,则中序遍历左子树,然后访问成员,继续访问中序遍历右子树,知道二叉树为空。
void Descendants(TriTree *t)函数的思想:
查找一个成员的子孙后代,首先判断当前结点是否存在左孩子,如果存在则调用InOrder()函数,中序遍历当前结点的左右子树,直到当前结点左孩子为空。
12.查找成员堂兄弟函数:
Void Consin(TriTree *t)一个成员的堂兄弟为其双亲的双亲节点的所有孩子的孩子(该成员除外)。
图7 查找成员堂兄弟_树形结构
如果结点t的双亲和双亲的双亲(爷爷)都存在。首先考虑爷爷的左孩子,即双亲1(t=t->parent->parent->lchild)。
如果爷爷的左孩子不是结点t的双亲,那么爷爷还有其他的孩子,如:双亲2、双亲3。
先对爷爷的左孩子的左孩子结点访问(temp=t->lchild),如果不是结点t,就输出,即输出堂兄1。
接着同样,对爷爷左孩子的左孩子的右孩子(输出堂兄2)、右孩子(t=t->rchild)的右孩子一直访问下去(输出兄弟c),直到无右孩子为止。
如果爷爷还有其他孩子,那么就对爷爷的左孩子的右孩子、爷爷的左孩子的右孩子的右孩子…即对爷爷的其他孩子做相同的处理。
13.查找一个成员的所有孩子函数:
Void Children(TriTree *t)一个成员的所有孩子包括左孩子和左孩子的右孩子、左孩子的右孩子的右孩子…直到右孩子为空为止。
基本思想:
①判断结点t是否有左孩子,如果没有,输出没有孩子。
②如果有左孩子,输出左孩子的信息。
③判断左孩子的右孩子是否为空,若不为空(存在右孩子),输出右孩子的右孩子的信息。
④循环判断结点是否有右孩子,有就输出,直到右孩子为空。
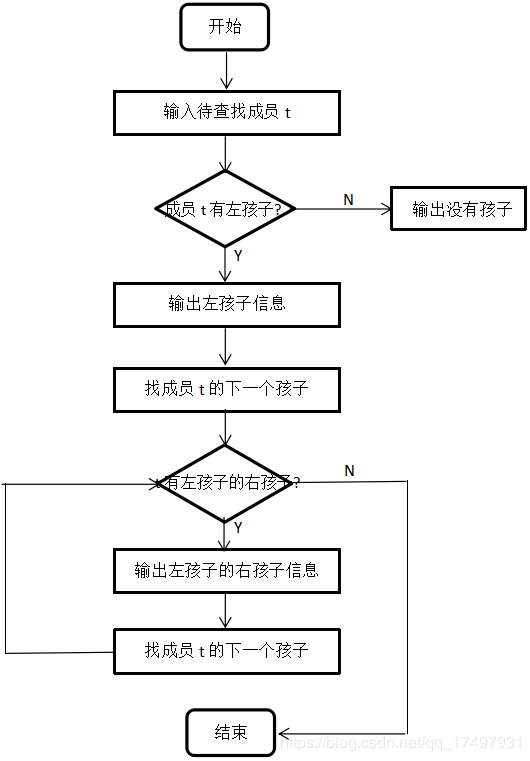
程序流程图:
图8 查找所有成员孩子
函数描述:
首先判断结点t是否有左孩子,如果没有,输出没有孩子;如果有左孩子,输出左孩子的信息,然后判断左孩子的右孩子是否为空,若不为空(存在右孩子),输出左孩子的右孩子的信息,接着循环判断结点是否有右孩子,有就输出,直到右孩子为空。
14.主函数:统筹调用各个函数实现相应功能
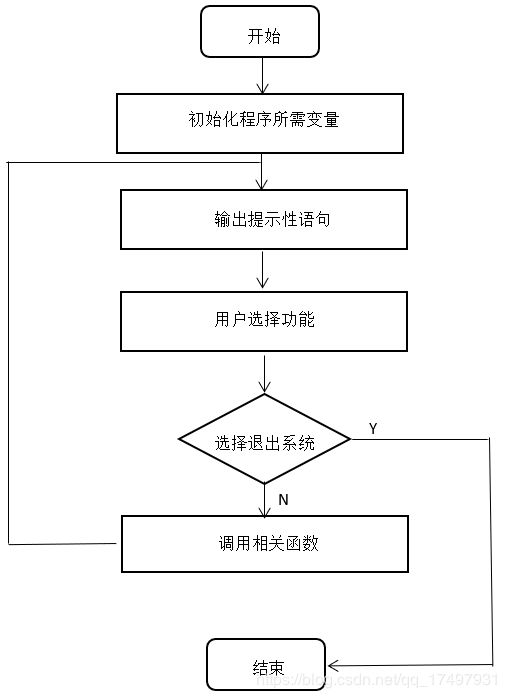
int main(int argc,char *argv[])程序流程图:
图9 主函数流程图
首先,初始化程序中所需要的变量;在输出用户界面,等待用户进行操作。用户通过键盘方向键选择功能,根据用户选择的功能调用相关的函数。
四、测试结果
(一)测试用例
表1 测试用例表
| 测试用例ID |
测试功能 |
测试步骤 |
预期结果 |
备注 |
| 1 |
新建一个家族关系 |
选择新建家族关系 |
新建一个家族关系,名字为a |
家族a如果已经存在,可以直接打开也可以重新建立 |
| 2 |
打开一个家族关系 |
选择打开家族关系 |
打开a的家族关系 |
无 |
| 3 |
添加新成员的信息 |
选择添加新成员 |
为d添加一个孩子z |
先输入孩子再输入双亲的名字 |
| 4 |
查找一个成员的祖先 |
选择查找成员祖先 |
返回h的祖先a |
无 |
| 5 |
查找一个成员的祖先路径 |
选择查找祖先路径 |
返回h的祖先路径z->d->a |
以路径的格式返回 |
| 6 |
确定一个成员是第几代 |
选择成员是第几代 |
返回z为第三代 |
返回数字 |
| 7 |
查找一个成员的双亲 |
选择查找成员双亲 |
返回z的双亲为d |
无 |
| 8 |
查找一个成员的兄弟 |
选择查找成员兄弟 |
返回z没有兄弟 |
兄弟 |
| 9 |
查找一个成员的堂兄弟 |
选择查找堂兄弟 |
返回z的堂兄弟e.f.g |
堂兄 |
| 10 |
查找一个成员的孩子 |
选择查找成员孩子 |
返回z没有孩子 |
成员可能没有孩子 |
| 11 |
查找一个成员的子孙后代 |
选择查找子孙后代 |
返回z没有后代 |
成员可能没有后代 |
| 12 |
退出系统 |
选择退出 |
系统退出 |
无 |
1、新建一个家族关系
图10 新建家族关系
需求测试:
用户根据程序需求的格式进行输入,兄弟输入结束以@为标志,结束标志为#。
界面测试:
选择新建家族关系,输入新建家族关系名称a(建立家族关系并且名字为a),当家族关系不存在,程序界面给用户提示“请按层次输入结点,每个结点信息占一行,兄弟输入结束以@为标志,结束标志为#”,输入正确的家族关系并以#结束,系统界面提示“家族关系已成功建立”。
选择新建家族关系,输入新建家族关系名称a,家族关系已经存在,系统界面提示“家族关系已存在,重新建立按Y,直接打开按N”;
功能测试:
选择新建家族关系,程序提示请输入家族名称,输入家族名称a,程序提示“请按层次输入结点,每个结点信息占一行,兄弟输入结束以@为标志,结束标志为#”,再次输入
a
@
b
c
d
@
e
@
f
g
@
@
h
i
@
#程序提示家族关系已经建立。
选择新建家族关系,程序提示“家族关系已存在,重新建立按Y,直接打开按N”,输入N,程序返回家族关系已成功打开。
选择新建家族关系,程序提示“家族关系已存在,重新建立按Y,直接打开按N”,输入Y,程序提示“请按层次输入结点,每个结点信息占一行,兄弟输入结束以@为标志,结束标志为#”,再次输入
a
@
b
c
d
@
e
@
f
g
@
@
h
i
@
#程序提示家族关系已经建立。
可靠性:输入家族关系后正确的存储家族关系,不能出现位置错乱问题。
易用性:输入的格式是否符合正常的家族关系格式。
用户文档:输入方式的格式、限制、条件等有详细描述。
压力测试:多次输入家族关系,并且多次输入同名字的家族关系,确保程序正确性。
2、打开一个家族关系
图11 打开家族关系
需求测试:
选择打开家族关系,打开一个家族关系,如果需要打开的家族关系已经存在,则显示“家族关系已成功打开”。如果家族关系不存在则显示“家族关系不存在”。
界面测试:
选择打开家族关系,并输入a(打开名字为a的家族关系),当家族关系已经存在,程序界面给用户提示“家族关系已成功打开”,输入不存在的家族关系,程序界面给用户显示“家族关系不存在”。
功能测试:
选择打开家族关系,请输入家族关系时输入a,家族关系已打开。选择打开家族关系,请输入家族关系时输入aaa,,显示aaa的家族关系不存在。
可靠性:多次打开家族关系,最后操作的家族关系为最后打开的家族关系。
易用性:输入打开的家族关系名称直接打开。
用户文档:输入方式的格式、限制、条件等有详细描述。
压力测试:多次打开家族关系,确保每一次都成功打开。
3、添加新成员的信息
图12 添加一个新成员
需求测试:
选择添加新成员,添加一个新的家族成员,依次输入新成员的名字,再输入双亲的名字,当输入双亲的名字存在时,程序提示成员添加成功,当输入的双亲节点的名字不存在时,程序提示该成员不存在。
界面测试:
选择添加新成员,程序界面提示“请输入要添加成员的名字”,输入新成员的名字并回车,程序界面提示“请输入其父亲的名字”,当输入新成员的父亲存在时,程序界面提示“新成员添加成功”,当新添加的成员双亲结点不存在时,程序界面提示“该成员不存在,不能为其添加子女”。
功能测试:
选择添加新成员,依次输入z,再次输入d。程序提示新成员添加成功。选择添加新成员,依次输入x,再次输入aaa,程序提示aaa不存在,不能为其添加子女。
可靠性:多次输入新成员添加的新成员家族关系正确。
易用性:一次输入新成员和其父亲的名字,即可添加成功。
用户文档:输入方式的格式、限制、条件等有详细描述。
压力测试:多次输入新成员,确保添加新成员后家族关系正确。
4、查找一个成员的祖先
图13 查找一个成员的祖先
需求测试:
选择查找成员祖先,查找一个成员的祖先。
界面测试:
选择查找成员祖先,程序显示请输入成员名字,程序界面该成员的祖先为a。
选择查找成员祖先,程序显示请输入成员名字,程序界面提示该成员不存在。
功能测试:
选择查找成员祖先,程序显示a。
可靠性:同一个家族中所有人的祖先都为同一人。
易用性:输入成员便可查看祖先。
用户文档:输入方式的格式、限制、条件等有详细描述。
5、查找一个成员的祖先路径
图14 查找一个成员的祖先路径
需求测试:
选择查找祖先路径,程序应清晰的返回该成员到其祖先的路径,用->指示。
界面测试:
选择查找祖先路径,请输入成员名称,输入成员,若成员存在,返回其到祖先的路基。
选择查找祖先路径,请输入成员名称,输入成员,若成员不存在,返回该成员不存在。
功能测试:
选择查找祖先路径,输入成员名称z,程序返回z->d->a。
选择查找祖先路径,输入成员名称zzz,程序返回该成员不存在。
可靠性:输入任何一个存在的成员都应该返回其到祖先的路径。
易用性:一次输入成员的名字即可返回到祖先的路径。
用户文档:输入方式的格式、限制、条件等有详细描述。
6、确定一个成员是第几代
图15 查找一个成员是第几代
需求测试:
选择成员是第几代,可以查看当前成员为第几代成员。
界面测试:
选择成员是第几代,程序界面提示输入成员名称,如果z存在,返回z是第几代。如果z不存在,程序提示该成员不存在。
功能测试:
选择成员是第几代,输入成员名字z,程序提示z为第三代。
选择成员是第几代,输入成员名字zzz,程序提示该成员不存在。
可靠性:输入家族中的成员都可以查看为第几代成员。
易用性:输入成员名返回数字为第几代。
用户文档:输入方式的格式、限制、条件等有详细描述。
7、查找一个成员的双亲
图16 查找一个成员的双亲
需求测试:
选择查找成员双亲,查看一个成员的双亲结点。
界面测试:
选择查找成员双亲,程序提示请输入成员名称,输入成员名称,如果该成员存在,返回该成员的双亲。如果该成元宝不存在,提示该成员不存在。
功能测试:
选择查找成员双亲,输入查找的成员z,程序提示z的双亲为d。
选择查找成员双亲,输入查找的成员zzz,程序提示该成员不存在。
可靠性:输入一个成员,可以查看双亲结点。
用户文档:输入方式的格式、限制、条件等有详细描述。
8、查找一个成员的兄弟
图17 查找一个成员的兄弟
需求测试:
选择查找成员兄弟,查看一个成员的兄弟。
界面测试:
选择查找成员兄弟,程序提示请输入成员名字,输入成员的名字,如果该成员不存在,提示该成员不存在。如果该成员存在,并且该成员存在兄弟,返回该成员的兄弟名字,如果该成员没有兄弟,返回该成员无兄弟。
功能测试:
选择查找成员兄弟,输入zzz,返回该成员不存在。
选择查找成员兄弟,输入z,返回该z无兄弟。
选择查找成员兄弟,输入d,返回d的所有兄弟bc。
可靠性:输入一个成员,可以查看兄弟结点。
用户文档:输入方式的格式、限制、条件等有详细描述。
9、查找一个成员的堂兄弟
图18 查找一个成员的堂兄弟
需求测试:
选择查找堂兄弟,查看一个成员的堂兄弟。
界面测试:
选择查找堂兄弟,程序提示请输入成员名字,输入成员的名字,如果该成员不存在,提示该成员不存在。如果该成员存在,并且该成员存在堂兄弟,返回该成员的堂兄弟名字,如果该成员没有堂兄弟,返回该成员无堂兄弟。
功能测试:
选择查找成员堂兄弟,输入zzz,返回该成员不存在。
选择查找成员堂兄弟,输入z,返回z的所有堂兄弟eg。
可靠性:输入一个成员,可以查看堂兄弟结点。
用户文档:输入方式的格式、限制、条件等有详细描述。
10、查找一个成员的孩子
图19 查找一个成员的孩子
需求测试:
选择查找成员孩子,查看一个成员的孩子。
界面测试:
选择查找成员孩子,程序提示输入成员的名称,输入成员的名字,若该成员不存在,则提示该成员不存在,若该成员存在,但是没有孩子,程序提示该成员没有孩子,若成员有孩子,则显示该成员的所有孩子。
功能测试:
选择查找成员孩子,输入zzz,返回该成员不存在。
选择查找成员孩子,输入z,返回z无孩子。
选择查找成员孩子,输入d,返回d的所有孩子z。
可靠性:输入一个成员,可以查看孩子结点。
用户文档:输入方式的格式、限制、条件等有详细描述。
11、查找一个成员的子孙后代
图20 查找一个成员的后代
需求测试:
选择查找子孙后代,查看一个成员的所以子孙后代。
界面测试:
选择查找子孙后代,程序提示输入成员的名称,输入成员的名字,若该成员不存在,则提示该成员不存在,若该成员存在,但是没有子孙后代,程序提示该成员没有后代,若成员有后代,则显示该成员的所有后代的名字。
功能测试:
选择查找成员孩子,输入zzz,返回该成员不存在。
选择查找成员孩子,输入z,返回z无后代。
选择查找成员孩子,输入d,返回d的所有子孙后代z。
可靠性:输入一个成员,可以查看子孙后代。
用户文档:输入方式的格式、限制、条件等有详细描述。
12、退出系统
结束程序输入,成功退出程序。
(二)执行错误
测试过程:
运行程序出现编译错误。
1.第一次出现的错误及原因:
Open()方法未声明。
open()方法已经创建,未声明引用。
TriTreeCreate()方法未声明。
TriTreeCreate()方法已经创建,未声明引用。
解决方法:
创建方法引用说明。
2.第二次出现的错误及原因:
若创建家族关系树时不输入@,程序非法结束。创建三叉链表时程序非正常终止。
逻辑判断输入的为#结束输入,输入的为@为下一个双亲结点的孩子。若没有输入@,函数一直循环判断@的循环,即使输入#也不会判断到结束。数组最大[20],数组下标越界,函数错误。
解决方法:
固定输入格式,如下:
1
@
2
3
4
@
#以确保结束输入之前当前结点的兄弟结点输入结束。
3.第三次出现的错误及原因:
exit()方法无法退出
![]()
当用户输入完成一次结束时,检测用户输入的是否真确或者符合要求,当用户输入错误或者程序执行结束时返回while()让用户重新输入时,当前while()结束的位置在switch()之前,当用户输入需要执行的函数时程序并不会执行switch()里边的方法调用,而直接返回让用户重新输入。
应从return之前返回,确保程序执行完函数调用。而不应该从switch()之前返回。
(三)逻辑错误
1、open()方法错误
进行家族关系操作之前需要新建或者打开一个家族关系。
测试过程:
运行程序,输入”open(a)”并回车。
预期结果:
程序正确运行,并显示家族关系已打开。
实际结果:
程序停止工作。
修改过程:
open()方法用于打开三叉链表;
如果三叉链表不存在则新建一个三叉链表直接打开,如果三叉链表存在则打开文件中的三叉链表。
通过两个函数引用可见一个有参数一个没有参数,而程序中只给出一个没有参数的方法,所以当打开文件中的三叉链表时程序出错,结束工作。
通过函数重载,获得有参的重载函数。
2、检测方法参数的必要性以及正确性
建立家族关系添加家族成员等一系列操作都需要输入所需的参数,这里需要保证参数的必要性,正确性。
测试过程:
创建一个新的家族关系时。运行程序,输入”create”,回车。
预期结果:
家族关系没有名字,家族关系创建失败。
实际结果:
家族关系已成功建立。
同样打开一个没有名字文件输入”open”,结果家族关系打开成功。
修改过程:
取得输入的参数
首先,如果输入的方法不存在,则应该显示无匹配函数,请重新输入!。
其次判断输入的方法是否需要参数,如append()和exit()不需要输入参数,可以跳过。其他的函数则需要输入函数,如果没有参数则显示请输入参数!!!并要求用户重新输入。
3、append()添加失败
添加新成员时,要求“请输入要添加的成员和其父亲,以回车分隔!”,输入新成员名之后提示成员不存在。
测试过程:
运行程序。输入“append”,输入新成员姓名“wang”,输入新成员父亲姓名“zhang”。
预期结果:
程序可以正常运行,提示输入“请输入要输入的成员名字”。输入新成员名称,提示“请输入其父亲的名字”,输入其父亲的名字,显示新成员添加成功。
实际结果:
提示“该成员不存在!”。
修改过程:
程序提示先输入新成员名字,再输入其父亲的名字。
原本代码结构:
可见输入的新成员和父亲名称只获取了父亲的名称,并没有获取新成员的名称,应为先获取新成员的名字,然后检测其父亲结点是否存在,加入存在则添加成功,加入不存在则应显示“该成员不存在”。
修改代码结构:
4、append()添加成员#消失
程序提供给家族添加一个新成员。添加成员后应保证结构正确。
测试过程:
输入“append”,输入新成员姓名“wang”,输入新成员父亲姓名“zhang”
预期结果:
新成员添加成功,且添加位置正常。
实际结果:
新成员添加成功,存储文件结束标志“#”消失。再次打开该家族关系,由于没有家族结束标志#,一直读取家族成员,直至数组下标越界,程序错误结束。
修改过程:
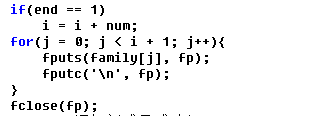
查看添加的成员是否成功,添加一个新成员,其余成员位置往后移动一个。
j 修改方法: j<=i+1让#也后移一位,保证#不被覆盖。 本程序巧妙地将家族关系信息转换为二叉树信息,利用队列来创建三叉链表,存储家族关系信息,能够将信息存入文件中,以便下次访问,能对当前家族添加新成员,实现动态查询。在家族关系查询中包含了许多查询功能,通过输入不同的命令和参数有选择的实现各种查询,操作方便,实用性强。在编写程序时,可加入修改成员信息功能,并能及时更新保存。 通过本次课程设计,让我们成员对C语言和数据结构有了一次比较深入的复习和整理,同时也加深了我对程序的理解,特别是对一个大程序,来怎样对它进行编写。本次课程设计是我们成员认清了今后应该努力地方向,同时也暴漏了自己在平时学习中的不足。 通过此次设计是我们成员对数据结构有了更深的理解。在编写某个具体程序时,应根据其数据特点选择适当的逻辑结构、存储结构及其相应的算法,提高算法执行的效率。在编写程序时,应特别注意编写的程序结构要清楚,并且正确易读,要符合规范,平时就要这样要求自己。本课程设计在一定程度上也培养了我们小组成员自己的数据抽象能力。 总之,本次课程设计使我们受益匪浅,学到不少课本之外的知识,也认识到自己的不足。在以后需要加强自己训练,学以致用,学会自我总结,吸取教训,积累经验,在学习和实践中不断提升自己。 五、分析与探讨
附录 主要源代码
/////////建立家族关系并存入文件/////////
TriTree * Create(DataType familyname[MAXNUM]){
int i = 0;
DataType ch,str[MAXNUM]; //ch存储输入的y或n,str存储输入的字符串
TriTree * t;
FILE * fp;
strcpy(fname, familyname); //以家族名为本文件名存储
strcat(fname,".txt");
fp = fopen(fname, "r"); //以读取方式打开
if(fp){ //文件已存在
fclose(fp);
printf("\n\n\n\t\t\t%s的家族关系已存在!重新建立请按“Y”,直接打开请按“N”\n",familyname);
ch = getchar();
getchar(); //接收回车
if(ch == 'N' || ch == 'n'){
t = Open(familyname); //直接打开
return t;
}
}
if(!fp || ch == 'Y' || ch == 'y'){//重新建立
fp = fopen(fname, "w"); //以写入方式打开文件,不存在则新建
system("cls");
printf("\t *\t 请按层次输入节点,每个节点信息占一行 *\n");
printf("\t *\t 兄弟输入结束以“@”为标志,结束标志为“#” *\n");
printf("\n\t请输入: ");
gets(str);
fputs(str,fp);
fputc('\n',fp);
strcpy(family[i], str); //将成员信息存储到字符数组中
i++; //family数组下标后移
while(str[0] != '#'){
printf("\t请输入: "); //以点提示符提示继续输入
gets(str);
fputs(str, fp); //写到文件中,每个信息占一行
fputc('\n',fp);
strcpy(family[i], str); //将成员信息存储到字符数组中
i++; //family数组下标后移
}
fclose(fp); //关闭文件
t = TriTreeCreate(); //根据family数组信息创建三叉树
printf("\n\n\t\t\t家族关系已成功建立!\n");
return t;
}
}
/////////建立家族关系树/////////
TriTree * TriTreeCreate(){
TriTree * t, *x = NULL, *tree, *root = NULL;
LinkQueue * q = LQueueCreateEmpty();//建立一个空队列,存储指向树的指针
int i = 0, flag = 0, start = 0;
DataType str[MAXNUM]; //存放family数组中信息
strcpy(str, family[i]);
i++;
while(str[0] != '#'){ //没遇到结束标志
while(str[0] != '@'){ //没遇到兄弟节点继续查找
if(root == NULL){ //空树
root = (TriTree * )malloc(sizeof(TriTree));
strcpy(root->data, str);
root->parent = NULL;
root->lchild = NULL;
root->rchild = NULL;
LQueueEnQueue(q, root);
tree = root;
} else{ //不为空
t = (TriTree * )malloc(sizeof(TriTree));
strcpy(t->data, str);
t->lchild = NULL;
t->rchild = NULL;
t->parent = LQueueGetFront(q);//当前节点的双亲为队头元素
LQueueEnQueue(q, t);
if(!flag)
root->lchild = t;
else
root->rchild = t;
root = t;
}
flag = 1;
strcpy(str, family[i]);
i++;
}
if(start != 0){ //标记不是第一次出现“@”
LQueueDeQueue(q, x);
if(q->front != NULL)
root = LQueueGetFront(q);//root为队头元素
}
start = 1; //标记已出现过“@”
flag = 0; //“@”后面的结点一定为左孩子
strcpy(str, family[i]);
i++;
}
return tree;
}
/////////打开一个家族关系/////////
TriTree * Open(DataType familyname[MAXNUM]){
int i = 0, j = 0;
DataType ch;
FILE * fp;
TriTree * t;
strcpy(fname, familyname); //以家族名为文本名存储
strcat(fname, ".txt");
fp = fopen(fname, "r");
if(fp == NULL){
printf("\n\n\t\t\t%s的家族关系不存在!\n",familyname);
return NULL;
} else{
ch = fgetc(fp); //按字符读取文件
while(ch!=EOF){ //读到文件尾结束
if(ch != '\n'){
family[i][j] = ch;
j++; //将文件信息存储到family数组中
} else{
family[i][j] = '\0';
i++; //行下标后移
j = 0; //列下标归零
}
ch = fgetc(fp);
}
fclose(fp);
t = TriTreeCreate(family); //建立三叉链表
printf("\n\n\t\t\t家族关系已打开!\n");
return t;
}
}
/////////向家族中添加一个新成员/////////
void Append(TriTree *t){
int i = 0, j, parpos = 1, curpos, num, end = 0, count = -1;
DataType chi[MAXNUM], par[MAXNUM];
TriTree * tpar, * temp;
FILE * fp;
printf("\n\n\t\t\t请输入要添加的成员的名字:");
gets(chi);
printf("\n\t\t\t请输入其父亲的名字:");
gets(par);
tpar = Search(t, par);
if(tpar == NULL)
printf("\n\n\t\t\t%s成员不存在,不能为其添加子女!\n",par);
else{
temp = (TriTree * )malloc(sizeof(TriTree));
temp->parent = tpar;
strcpy(temp->data, chi);
temp->lchild = NULL;
temp->rchild = NULL;
if(tpar->lchild != 0){
tpar = tpar->lchild;
while(tpar->rchild != NULL)
tpar = tpar->rchild;
tpar->rchild = temp;
} else
tpar->lchild = temp;
fp = fopen(fname,"w");
if(fp != 0){
while(strcmp(par, family[i]) != 0 && family[i][0] != '#'){
if(family[i][0] != '@')
parpos++;
i++;
}
i = 0;
while(family[i][0] != '#'){
if(family[i][0] == '@')
count++;
if(count == parpos)
curpos = i;
i++;
}
if(count < parpos){
num = parpos - count;
for(j = i; j <= i + num; j++)
strcpy(family[j], "@\0");
strcpy(family[i + num + 1], "#\0");
strcpy(family[i + num - 1], chi);
end = 1;
} else{
for(j = i; j >= curpos; j--)
strcpy(family[j+1], family[j]);
strcpy(family[curpos], chi);
}
if(end == 1)
i = i + num;
for(j = 0; j <= i + 1; j++){
fputs(family[j], fp);
fputc('\n', fp);
}
fclose(fp);
printf("\n\n\t\t\t添加新成员成功!\n");
} else
printf("\n\n\t\t\t添加新成员失败!\n");
}
}
/////////删除一个成员/////////
void txtDel(DataType str[]){
int i = 0, j;
FILE * fp;
fp = fopen(fname,"w");
if(fp != 0){
i = 0;
while(family[i][0] != '#')
i++;
for(j = 0; j <= i + 1; j++){
if(strcmp(family[j-1], "@\0") == 0 && strcmp(family[j+1], "@\0" == 0) j += 2;
if(strcmp(family[j], str) == 0) //如果找到,就j++跳过此元素
j++;
fputs(family[j], fp);
fputc('\n', fp);
}
fclose(fp);
}
}
void Delete(TriTree *t){
int i = 0, j, parpos = 1, curpos, num, end = 0, count = -1;
DataType chi[MAXNUM], par[MAXNUM];
TriTree * ta = t;
if(t->lchild){ //如果有孩子提示先删除孩子
printf("\n\n\t\t\t%s有孩子,请先删除其孩子!\n\n", t->data);
} else if(t->parent->lchild->data == t->data){
txtDel(t->data); //删除txt中记录
if(t->rchild)
t->parent->lchild = t->rchild;//删除其有右孩子 else
t->parent->lchild = NULL;//如果没有右孩子,删除其父节点的左孩子指针
free(t); //释放空间
printf("\n\n\t\t\t成员删除成功!\n\n");
} else{
if(t->parent->lchild->rchild) //其父亲做孩子有右孩子,也就是有兄弟
t = t->parent->lchild;//t只指向其父亲左孩子,也就是要删除成员的兄弟
while(ta->rchild){ //t有右孩子
if(ta->data == t->rchild->data){//判断要删除的成员是否是t的右孩子
txtDel(t->data); //删除txt内容
if(t->rchild)
t->parent->lchild = t->rchild;//删除其有右孩子 else
t->parent->lchild = NULL;
free(t); //释放空间
printf("\n\n\t\t\t成员删除成功!\n\n");
break;
} else{
t = t->rchild;
}
}
}
}
/////////查找一个成员的所有祖先路径/////////
void AncesstorPath(TriTree * t){
if(t->parent == NULL)
printf("\n\n\t\t\t%s无祖先!\n",t->data);
else{
printf("\n\n\t\t\t%s所有祖先路径:%s",t->data, t->data);
while(t->parent != NULL){ //若当前成员的双亲部署祖先,则继续查找
printf("-->%s", t->parent->data);
t = t->parent;
}
printf("\n");
}
}
/////////查找一个成员的兄弟/////////
void Brothers(TriTree * t, DataType str[]){
if(t->parent != NULL){
t = t->parent;
if(t->lchild && t->lchild->rchild){ //当前节点的左孩子及其右孩子都存在
printf("\n\n\t\t\t%s的所有兄弟有:",str);
t=t->lchild;
while(t){ //遍历当前成员做孩子的右子树
if(strcmp(t->data, str) != 0)
printf("%s ", t->data);
t = t->rchild;
}
printf("\n");
} else
printf("\n\n\t\t\t%s无兄弟!\n", str);
} else
printf("\n\n\t\t\t%s无兄弟!\n", str);
}
/////////13.查找一个成员的堂兄弟/////////
void Consin(TriTree * t){
int flag = 0;
TriTree * ch = t;
TriTree * temp;
if(t->parent && t->parent->parent){ //当前结点的双亲及其双亲都存在
t = t->parent->parent->lchild; //当前结点等于其祖先的第一个孩子
while(t){ //存在则继续查找
if(strcmp(t->data, ch->parent->data) != 0){ //不是同一结点
if(t->lchild){ //当前结点存在左孩子
temp = t->lchild;
while(temp){ //遍历当前结点左孩子的右子树
if(strcmp(temp->data,ch->data) != 0){
if(!flag) //第一次输入时先输出下句
printf("\n\n\t\t\t%s的堂兄弟:", ch->data);
printf("%s ", temp->data);
flag = 1;
}
temp = temp->rchild;//继续遍历右孩子
}
}
}
t = t->rchild; //继续遍历右孩子
}
printf("\n");
}
if(!flag) //标志没有输出结点
printf("\n\n\t\t\t%s无堂兄弟!\n", ch->data);
}
/////////查找一个成员的所有孩子/////////
void Children(TriTree * t){ //孩子兄弟表示法
if(t->lchild){
printf("\n\n\t\t\t%s的所有孩子有:", t->data);
t = t->lchild;
while(t){
printf("%s ",t->data);
t = t->rchild;
}
printf("\n");
} else
printf("\n\n\t\t\t%s无孩子!\n", t->data);
}
/////////查找一个成员的子孙后代/////////
//中序遍历
void InOrder(TriTree * t){
if(t){
InOrder(t->lchild); //中序遍历左子树
printf("%s ", t->data); //访问成员
InOrder(t->rchild); //中序遍历右子树
}
}
//查找一个成员的子孙后代
void Descendants(TriTree * t){
if(t->lchild){
printf("\n\n\t\t\t%s的所有子孙后代有:", t->data);
InOrder(t->lchild);
printf("\n");
} else
printf("\n\n\t\t\t%s无后代!\n", t->data);
}
/////////主函数/////////
int main()
{
while(1)
{
showmenu(hOut , menu , NR(menu) , index);
ret = get_userinput(&index , NR(menu));
if(ret == ESC)
break ;
if(ret == ENTER)
{
switch(index)
{
case 0: //创建家族关系
while(1){
printf("\n\n\n\t\t\t请输入家族名称:");
gets(str);
if(strlen(str) > 0)
break;
}
tree = Create(str);
start = 1;
Sleep(2000);
break;
case 1: //打开家族关系
while(1){
printf("\n\n\n\t\t\t请输入家族名称:");
gets(str);
if(strlen(str) > 0)
break;
}
tree = Open(str);
start = 1;
Sleep(2000);
break;
case 2: //添加新成员
noopen();
Append(tree);
Sleep(2000);
break;
case 3: //删除一个成员
noopen();
tempSearch();
Delete(temp);
Sleep(2000);
break;
case 4: //查找成员祖先
noopen();
tempSearch();
Ancesstor(tree);
Sleep(2000);
break;
case 5: //查找祖先路径
noopen();
tempSearch();
AncesstorPath(temp);
Sleep(2000);
break;
case 6: //成员是第几代
noopen();
tempSearch();
Generation(temp);
Sleep(2000);
break;
case 7: //查找成员双亲
noopen();
tempSearch();
Parent(temp);
Sleep(2000);
break;
case 8: //查找成员兄弟
noopen();
tempSearch();
Brothers(temp, str);
Sleep(2000);
break;
case 9: //查找堂兄弟
noopen();
tempSearch();
Consin(temp);
Sleep(2000);
break;
case 10: //查找成员孩子
noopen();
tempSearch();
Children(temp);
Sleep(2000);
break;
case 11: //查找子孙后代
noopen();
tempSearch();
Descendants(temp);
Sleep(2000);
break;
case 12: //退出
printf("\n\n\n\t\t\t ");
exit(OK);
}
}
}
return 0;
}原版Word下载:下载链接