【机器学习】模型评估与选择

内容大多来自

• 统计学习方法——李航

• 机器学习——周志华

  1. 统计学习三要素

  统计学习方法都是有模型、策略和算法构成的，也就是统计学习方法由三要素构成，可以简单地表示为：

方法=模型+策略+算法 方 法 = 模 型 + 策 略 + 算 法

构建一种统计学习方法就是确定具体的统计学习的三要素。

1.1 模型

  统计学习首要考虑的问题是学习什么样的模型，在监督学习过程中，模型就是所要学习的条件概率分布或是决策函数。模型的假设空间（hypothesis space）包含所有可能的条件概率分布或决策函数。例如，假设决策函数是输入变量的线性函数，那么模型的假设空间就是所有这些线性函数构成的函数集合。假设空间中的模型一般由无穷多个。

  假设空间用 F F 表示。假设空间可以定义为决策函数的集合：

F={f|Y=f(X)} F = { f | Y = f ( X ) }

其中， X X 和 Y Y 是定义在输入空间 X X 和输出空间 Y Y 上的变量。这是 F F 通常是有一个参数向量决定的函数族：

F={f|Y=fθ(X),θ∈Rn} F = { f | Y = f θ ( X ) , θ ∈ R n }

参数向量 θ θ 取值于 n n 维欧式空间 Rn R n ，称为参数空间（parameter space）。

  假设空间也可以定义为条件概率的集合：

F={P|P(Y|X)} F = { P | P ( Y | X ) }

其中， X X 和 Y Y 是定义在输入空间 X X 和输出空间 Y Y 上的随机变量。这时 F F 通常由一个参数向量决定的条件概率分布族：

F={P|Pθ(Y|X),θ∈Rn} F = { P | P θ ( Y | X ) , θ ∈ R n }

参数向量 θ θ 取值于 n n 维欧式空间 Rn R n ，称为参数空间（parameter space）。

1.2 策略

  有了模型的假设空间，统计徐诶需要考虑的是按照什么样的准则学习或选择最优的模型。统计学习的目标在于从假设空间中选取最优模型。

  首先引入损失函数与风险函数的概念。

• 损失函数：度量模型以此预测的好坏；
• 风险函数：度量平均一一下模型预测的好坏；

1.2.1 损失函数和风险函数

  监督学习问题是在假设空间 F F 中选取模型 f f 作为决策函数，对于给定的输入 X X ，由 f(X) f ( X ) 给出相应的输出 Y Y ，这个输出的预测值 f(X) f ( X ) 与真实值 Y Y 可能一致也可能不一致，用一个损失函数 (loss function) 或 代价函数 (cost function) 来度量预测错误的程度。损失函数是 f(X) f ( X ) 和 Y Y 的 非负实值函数，记做 L(Y,f(X)) L ( Y , f ( X ) ) .\

  统计学习中常用的损失函数有一下几种

• 0-1 损失函数 (0-1 loss function)

• 平方损失函数 (quadratic loss function)

• 绝对损失函数 (absolute loss function)

• 对数损失函数 (logarithmic loss function)
  

  L(Y,P(Y|X))=−logP(Y|X) L ( Y , P ( Y | X ) ) = − l o g P ( Y | X )

  损失函数值越小，模型也就越好，由于模型的输入，输出 (X,Y) ( X , Y ) 是随机变量，遵循联合分布 P(X,Y) P ( X , Y ) ，所以损失函数的期望是

Rexp(f)=Ep[L(Y,f(X))]=∫X×YL(y,f(x))P(x,y)dxdy R e x p ( f ) = E p [ L ( Y , f ( X ) ) ] = ∫ X × Y L ( y , f ( x ) ) P ( x , y ) d x d y

这是卢纶上模型 f(X) f ( X ) 关于联合分布 P(X,Y) P ( X , Y ) 的平均意义下的损失，称为 风险函数(risk function) 或 期望损失(expected loss)。

  学习的目标就是选择期望风险最小的模型。由于联合分布是未知的，因此期望风险不能直接计算。也正是因为不知道联合概率分布，所以才需要进行学习。这样一来，一方面根据期望风险最小学习模型要用到联合分布，另一方面联合分布优势位置的，所以监督学习就称为一个病态问题。

  给定一个训练数据集

T={(x1,y1),(x2,y2),...,(xN,yN)} T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) }

模型 f(X) f ( X ) 关于训练数据集的平均损失称为 经验风险(empirical risk)或 经验损失(empirical loss)，记做 Remp R e m p ：

Remp(f)=1N∑i=1NL(yi,f(xi)) R e m p ( f ) = 1 N ∑ i = 1 N L ( y i , f ( x i ) )

  期望风险 Rexp R e x p 是模型关于联合分布的期望损失，经验风险 Remp R e m p 是模型关于训练样本集的平均损失。根据大数定律，当样本容量 N N 趋向于无穷时，经验风险趋向于期望风险。所以一个很自然的想法就是利用经验风险估计期望风险。但是，由于现实中训练样本数目有限，甚至很小所以用经验风险估计期望风险常常并不理想，要对经验风险进行一定的较真。这就关系到监督学习的两个基本策略：经验风险最小化和结构风险最小化。

1.2.2 经验风险最小化与结构风险最小化

  在假设空间、损失函数以及训练数据集确定的情况下，经验风险函数式就可以确定。经验风险最小化(empirical risk minimization, ERM) 的策略认为，经验风险最小的模型是最优的模型。根据这一策略，按照经验风险最小化的模型就是求解最优化问题：

minf∈F1N∑i=1NL(yi,f(xi)) m i n f ∈ F 1 N ∑ i = 1 N L ( y i , f ( x i ) )

其中， F F 是假设空间。

  当样本容量足够大的时候，经验风险最小化能够保证有很好的学习效果，在显示中野被广泛采用。比如，极大似然估计就是经验风险最小化的一个例子。当模型是条件概率分布，损失函数是对数损失函数时，经验风险最小化就等价于极大似然估计。

  但是，当样本容量很小时，经验风险最小挂学习的效果就未必很好，会产生过拟合的现象。

  结构风险最小化(structural risk minimization,SRM) 是为了防止过拟合而提出来的策略。结构风险最小化等价于正则化（regularization）。结构风险在经验风险上加上表示模型复杂度的正则化项（regularizer）或罚项(penalty term)。在假设空间、损失函数以及训练数据集确定的情况下，结构风险的定义是：

Rsrm(f)=1N∑i=1NL(yi,f(xi))+λJ(f) R s r m ( f ) = 1 N ∑ i = 1 N L ( y i , f ( x i ) ) + λ J ( f )

其中， J(f) J ( f ) 是模型的复杂度，是定义在假设空间 F F 上的泛函。模型 f f 越复杂，复杂度 J(f) J ( f ) 也就越大；反之，模型 f f 越简单，复杂度 J(f) J ( f ) 也就越小。也就是说，度咋读表示了对复杂模型的惩罚。 λ≥0 λ ≥ 0 是系数，用以权衡经验风险和模型复杂程度。结构风险小需要经验风险与模型复杂度同时小。结构风险小的模型往往队训练数据以及位置的测试数据都有比较好的预测。

  结构风险最小化的策略认为结构风险最小的模型是最优的模型，所以要求最幽默型，就是求解最优化问题：

minf∈F1N∑i=1NL(yi,f(xi))+λJ(f) m i n f ∈ F 1 N ∑ i = 1 N L ( y i , f ( x i ) ) + λ J ( f )

  这样，监督学习问题就变成了经验风险或结构风险函数的自由化问题。这是为经验或结构风险函数是最优化的目标函数。

1.3 算法

  算法是指学习模型的具体计算方法。统计学习基于训练数据集，根据学习策略，从假设空间中选择最幽默型，最后需要考虑使用什么样的计算方法求解最优模型。

  这是，统计学习问题归结为最优化问题，统计学习的算法成为求解最优化问题的算法。如果最优化问题有显式的解析解，这个最优化问题就比较简单。但通常解析解不存在，这就需要用数值计算的方法进行求解。如何保证找到全局最优解，并使求解的过程非常搞笑，就成为一个重要问题。

2. 性能度量

  对学习器的泛化性能进行评估，不仅需要有效可行的实验估计方法，还需要有衡量模型泛化性能的评价标准，这就是性能度量。性能度量反应了任务的额需求，在对比不同模型的能力时，使用不同的性能度量往往会导致不同的评判结果，这意味着模型的 “好坏” 是相对的，什么样的模型是好的，不仅缺绝育算法和数据，还决定于任务需求。

2.1 错误率与精度

  错误率与精度都是既适用于二分类任务，也适用于多分类任务。错误率是分类错误的样本占样本总数的比例，精度则是分类正确的样本数占样本总数的比例。对于样例集 D，分类的错误率定义为：

E(f;D)=1m∑i=1mI(f(xi)≠yi) E ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) ≠ y i )

精度则定义为：

acc(f;D)=1m∑i=1mI(f(xi)=yi)   =1−E(f;D) a c c ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) = y i )       = 1 − E ( f ; D )

更一般的，对于数据分布 D D 和概率密度函数 p(⋅) p ( · ) ，错误率与精度可分别描述为

E(f;D)=∫x∼DI(f(x)≠y)p(x)dx E ( f ; D ) = ∫ x ∼ D I ( f ( x ) ≠ y ) p ( x ) d x

精度为：

E(f;D)=∫x∼DI(f(x)=y)p(x)dx=1−E(f;D)       E ( f ; D ) = ∫ x ∼ D I ( f ( x ) = y ) p ( x ) d x = 1 − E ( f ; D )            

2.2 查准率，查全率与 F1

  在信息检索中，我们经常会关心 “检索出的信息有多少比例是用户感兴趣的”，“用户感兴趣的信息中有多少倍检索出来了”。查准率（precision）与 查全率（recall）是更为实用与此类需求的性能度量。

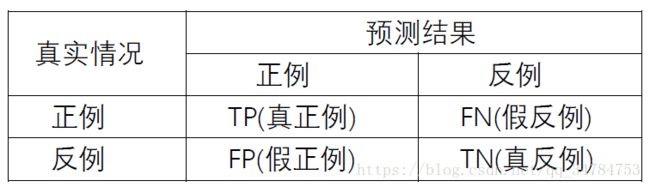
  对于二分类问题，可以将样例格局其真实类别与学习器预测类别的组合划分为 真正例(true positive)、假正例（false positive）、真反例（true negativve）和 假反例（false negative）这四种情形，这里分别令 TP,FP,TN,FN T P , F P , T N , F N 分别表示其对应的样例数，则显然有 TP+FP+TN+FN=  T P + F P + T N + F N =   样例总数。分类结果的混淆矩阵如下所示：

查准率 P 与 查全率 R 分别定义为：

P=TPTP+FP P = T P T P + F P

R:

R=TPTP+FN R = T P T P + F N

  差准率与查全率是一对矛盾的度量。一般来说，查准率较高时，查全率往往偏低，而查全率较高时，查准率往往偏低。

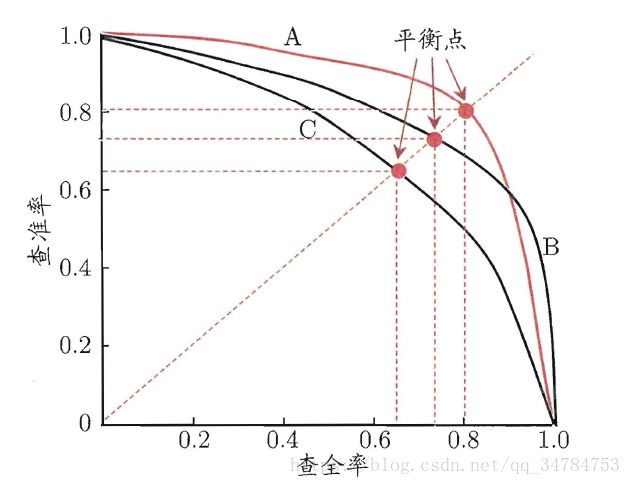
  根绝学习器预测结果对样例进行排序，排在前面的是学习器认为“最可能” 是正例的样本，排在最后的则是学习器认为“最不可能”是正例的样本。按照这个顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率，查准率。以查准率为纵轴，查全率为横轴进行作图，也就得到了“查准率-查全率” 曲线，简称 “P-R” 曲线，简称 P-R 图。

P-R 图能够直观的显示出学习器在样本总体上的查全率、查准率。在进行比较式，如果一个学习器 P-R 曲线被另一个学习器的曲线完全包围住，则可断言后者的性能由于前者。如果两个学习器的 P-R 曲线发生了交叉，则难以一般性的断言两者的优劣，只能在具体的查准率或 查全率条件下进行比较。一般这种时候，还可以比较 P-R 曲线下面积的大小，他在一定程度上表征了学习器在查准率和查全率取得相对 “双高” 的比例。但是这个值不太容易估算，因此，还设计了一些综合考虑查准率。查全率的性能度量。

  平衡点（BEP）就是这样一个度量，它是当 查准率=查全率 时的取值，哪个高认为哪个性能比较好。

但是 BEP 还是过于简化了一些，更为常用的是 F1 度量：

F1=2×P×RP+R=2×TP样例总数+TP−TN F 1 = 2 × P × R P + R = 2 × T P 样 例 总 数 + T P − T N

2.3 ROC 与 AUC

   ROC 的全称是“受试者工作特征” 曲线。和之前的 P-R 曲线类似，我们根据俄学习器的越策结果对杨丽进行排序，按照这个顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值，分别以他们为横、纵坐标作图，就得到了 “ROC” 曲线。ROC 曲线的纵轴是 “真正例率”（TPR），横轴是假正例率（FPR）.

TPR=TPTP+FN T P R = T P T P + F N

FPR:

FPR=FPTN+FP F P R = F P T N + F P

显示 ROC 曲线的图称为 “ROC 图”。下图给出了示意图：

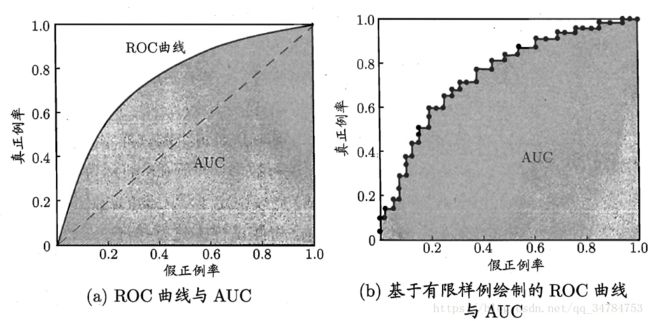
  上图中的对角线对应于 “随机猜测”模型，而点 （0,1）则对应于将所有正例排在所有反例之前的理想模型。上面右图中是利用有限数据绘制的 ROC 曲线，因为数据有限，因此无法画出左图中的类似图像。

  在进行学习器的比较时，与 P-R 图类似，如果一个徐吸气的 ROC 曲线被另一个学习器的曲线完全“包住”，则可断言后者的性能优于前者；如果两个学习器的 ROC 曲线发生交叉，此时如果一定要进行比较，则使用 ROC 曲线下的面积作为判据比较合理。也就是 AUC(area under ROC curve)。