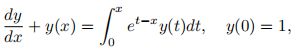《DeepXDE:a deep learning library for solving differential equations》梳理

本论文向我们介绍了一个求解微分方程的神经网络PINNs，和PINNs的Python库DeepXDE

摘要

1.PINNs(Physics-informed neural networks物理信息神经网络)
（1）它使用AD(automatic differentiation，自动微分)把PDE(partial differential equations，偏微分方程)嵌入到神经网络的损失函数中
（2）PINN的算法简单，而且可以求解不同类型的微分方程，对于求解逆问题(inverse problem)也很容易
（3）RAR(residual-based adaptive refinement，基于残差的自适应细化）改善PINNs的训练效率
2.DeepXDE, a Python library for PINNs

Introduction

1.PINNs
（1）a key step is to constrain the neural network to minimize the PDE residual
（2）求解PDEs的传统方法是基于网格的，如FDM(finite difference method)、FEM(finite element method)；神经网络使用自动微分方法，不需要网格
（3）PINNs可以求解不同类型的微分方程，对于求解逆问题只需改变极少的代码

2.DeepXDE
（1）是教学工具，也是研究工具
（2）基于CSG(constructive solid geometry)就可以支持复杂区域
（3） 用户通过callback function(回调函数）就可以很容易监督和修改求解过程

3.论文结构
重点是第二部分，是理论知识；在使用DeepXDE时，仔细看看第三部分

Algorithm and theory of PINNs

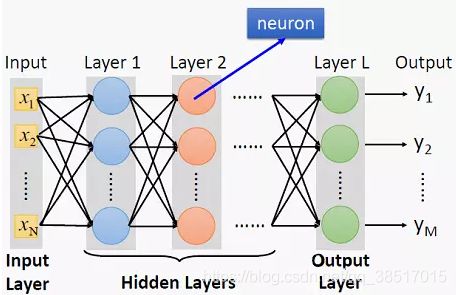
1.深度神经网络
（1）最简单的神经网络是FNN(feedforward neural network)，又被称为MLP(multilayer perceptron)
在本论文中还用了另一种神经网络ResNet(residual neural network), 对于深度网络来说很容易训练
（2）深度神经网络结构
下图是L层神经网络，又称为L-1层隐藏层神经网络

FNN定义如下

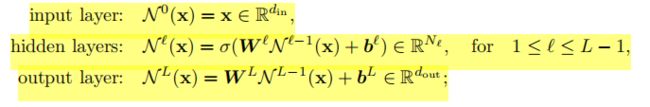
（一些符号的含义看论文，不方便粘贴，也不好打出来）

2.求解PDE的PINNs
(1)带有约束条件的偏微分方程如下

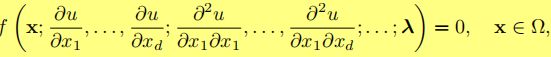
IC(initial condition初始条件)，可以看成狄利克雷条件的特殊情况
（2）
PINN求解PDE的原理图

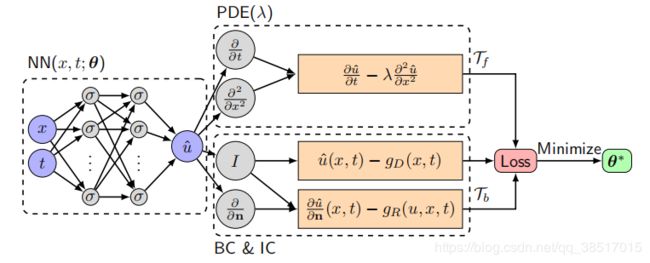
PINN求解PDE的算法步骤

步骤详述
step1:

step2：
得约束神经网络使之满足PDE和边界施加的条件
在整个域上约束很难，所以在一些离散点（训练数据）上约束

Tf、Tb被称为残差点(residual points)

step3: 损失函数

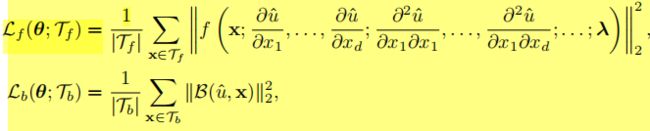
step4:
训练：通过最小化损失函数找到一个好的参数的过程
通常用基于梯度的优化器（如，梯度下降法）最小化损失函数

(3）三种策略选择残差点T

问题：当残差点数目很大时，每一次迭代计算损失函数和梯度花费很大
解决方案：不使用所有残差点，把这些残差点分成一小批一小批，每次迭代只用一批，这种方法称为mini-batch gradient descent

（4）最近研究表明，对于函数逼近，神经网络是低地频到高频学习目标函数的，但是PINNs的学习方式是所有频同时学习（这里的频不太了解指什么）

3.PINNs的逼近理论和误差分析
（1）逼近理论

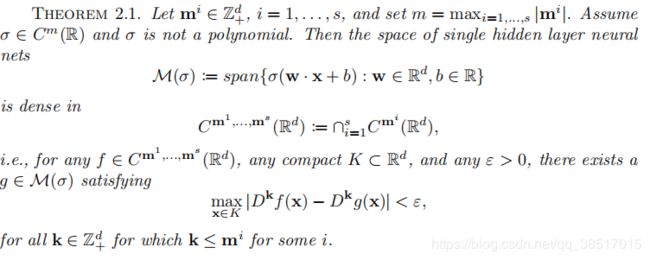
（这个定理没有看懂）
这个定理主要表明：具有足够神经元的前馈神经网络可以同时一致地逼近任意函数及其偏导数，就是存在可以求解PDE的神经网络
（2）误差分析

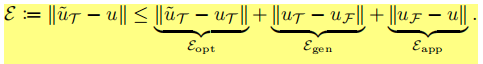
F表示可以由我们选择的神经网络结构表示的所有函数的族
u是PDE的解
uF是F中最接近u的函数
uT，因为训练是在T上
^uT，优化器中求出的逼近解
uF-u是逼近误差
uT-uF是全局误差
^uT-uT是优化误差

4.PINN和FEM的比较

更基本的是，PINNs提供的是非线性的逼近，而FEM提供的线性的逼近

5.PINNs求解IDEs(integro-differential equations,积分微分方程)
（1）IDEs如下

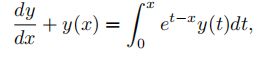
（2）对于微分仍用AD方法，对于积分使用传统方法，如高斯积分（注意会产生误差）

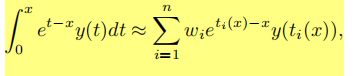
（3）原方程就转化为如下方程

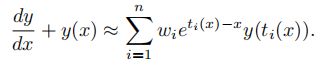
然后就可以用PINNs求解这个方程
下图是求解IDEs的PINNs算法的改进示意图，感觉相当于在原始PINNs的前面加一个预处理，把IDEs转化成普通的PDE

6.PINNs求解逆问题（不太清楚正问题和逆问题）
（1）在逆问题中增加了一些未知参数，同时也增加了在残差点上的额外信息

（2）损失函数


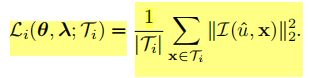
（3）

7.RAR(Residual-based adaptive refinement 基于残差的自适应细化)
问题：残差点通常是随机分布的，大多数情况下能得到较好的结果，但对于某些具有陡峭梯度解的偏微分方程，这可能没那么有效
解决：RAR方法
在PDE残差较大的位置添加更多的残差点
计算某点残差公式如下

什么时候停止：整个域的平均残差小于某个临界值（用户定义）
平均残差公式如下

(V是域的体积）
算法：

（第三步3中的add m new points with the largest residuals in S to T没有看懂）

DeepXDE的使用和定制化

1.使用


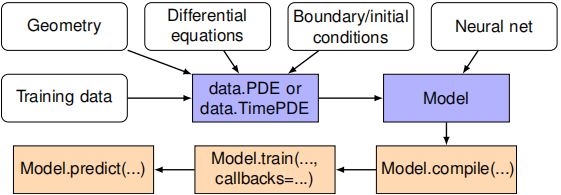
2.定制化
（1）geometry
a.DeepXDE中支持7种基本几何形状：interval,triangle,rectangle,polygon,disk,cuboid,sphere
b.还有CSG技术(constructive solid geometry)，|、-、&三种运算
c.还可以自己定制一个新的几何形状（未具体了解）

（2）neural networks
a.DeepXDE提供了两种神经网络：FNN，ResNet
b.用户也可以添加一个新的网络（未具体了解）

（3）callback
a.用户可以通过回调函数很容易监督神经网络的训练过程并做一些修改
b.常用回调函数有：ModelCheckpoint(保存模型),OperatorPredict(计算对输出应用算子之后的值),FirstDerivative(对输出求对输入的一阶导)等
c.用户也可以自定义一个回调函数(未具体了解)

demonstration examples

用PINNs和DeepXDE求解五个问题
（1）Poisson equation over an L-shaped domain

（2）RAR for Burgers equation

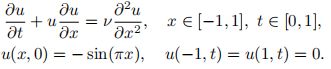
（3） Inverse problem for the Lorenz system

（4） Inverse problem for diffusion-reaction systems

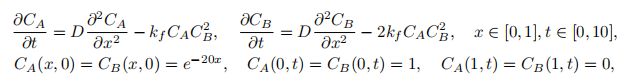
（5）Volterra IDE