leetcode hard模式专杀1269. Number of Ways to Stay in the Same Place After Some Steps
题干: https://leetcode.com/problems/number-of-ways-to-stay-in-the-same-place-after-some-steps/
前言:这题确实TMD有点难。
我一开始尝试用动态规划,但是没找好状态转移方程,可能是直觉不太好,然后尝试用回溯法来做。
之所以用回溯法,是因为我把每一步的决策看成三选一的决策动作,然后通过决策树的回溯遍历,自然可以得到想要的答案,可惜,这棵决策树可能很大,有多大想象一下,树根1个节点,第二层一个树开叉3个节点,第三层就开叉9, 第四层27,
第k层就3^(k-1)个,这种指数级别的增长相当恐怖。
果不其然当OJ使用的case达到二十几层的时候,我的程序就跑不动了。
不得已,只得再次尝试动态规划状态转移方程。
纸上多画画,最终找到一个可用的状态函数: 将用k步走到第i个下标的方案数即为d[k][i]
这个比较好做递推:d[k][i]=d[k-1][i-1]+d[k-1][i]+d[k-1][i+1]
这递推函数在i=0和i=最右侧下标时要做边界修正。
看起来这个递推函数比较好理解,相当于说既然第k步走到了i,那么第k-1步时要么在i-1, 要么在i,要么在i+1
这很合理,可是难就难在列出这么个玩意,哪来的信心它能真的递推出来(之前就发生过一次写完递推函数就stack overflow了)?
这就要靠继续推理了,这玩意的推理我觉得可以在纸上写写初始的几个值,例如dp[0][0],表示通过0次移动走到下标位0的位置,显然方案只有1个,而dp[0][x] (其中x>0)则表示不存在这样的方案,那么全部设置0即可。
这就相当于设置好了第0行
而根据递推函数,第k行的值全都是由第k-1行决定的,所以dp[1]行的值可以完全算出来,以此类推,dp[2]行的值也就可以递推出来。。。
最终只需要取算出来的矩阵的最后一行的第一个元素,即dp[steps][0]
根据这思路,写了下代码,发现tmd依然过不了OJ,不过这次的问题在空间复杂度,而非超时。
我这里只是初始化了一个二维矩阵啊,咋会空间超过呢?
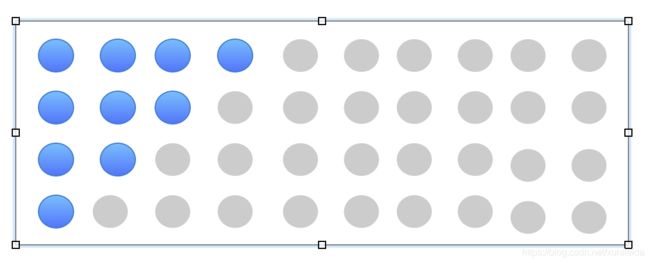
继续画了画图,既然我只需要最后一行的第0列,那么我们需要前面行的那些元素为依赖呢?如果把依赖的位置画一下,就会发现下图这种样子:
这个图中蓝色部分才是我们需要计算的,而灰色部分即使这个矩阵很大,我们用不着它们,去算他们,或者哪怕只是为它们创建存储空间都是浪费,所以我的方案是矩阵做个裁剪,裁到包含蓝色部分的最小矩阵就好。
代码如下:
package com.example.demo.leetcode;
public class NumberofWaystoStayntheSamePlaceAfterSomeSteps {
public int numWays(int steps, int arrLen) {
int M = (int)Math.pow(10,9) + 7;
long[][] dp = new long[steps+1][arrLen];
//初始条件
dp[0][0]=1;
for(int k = 1;k= 2*walk distance, 不满足的可以直接设置0
for(int i=1;i<=steps;i++){
for(int j=0;jsteps){
//不关心这样的位置,因为不可能
continue;
}
if(j==0){
dp[i][j] = (dp[i-1][j]+dp[i-1][j+1])%M;
}else if(j==arrLen-1){
dp[i][j] = (dp[i-1][j-1]+dp[i-1][j])%M;
}else{
dp[i][j] = (dp[i-1][j-1]+dp[i-1][j]+dp[i-1][j+1])%M;
}
}
}
return (int)dp[steps][0];
}
public static void main(String[] args) {
int steps = 2;
int arrLen = 4;
NumberofWaystoStayntheSamePlaceAfterSomeSteps demo = new NumberofWaystoStayntheSamePlaceAfterSomeSteps();
int ret = demo.numWays(steps, arrLen);
System.out.println(ret);
}
}
反思:多画图,对递推关系要反复审查,即要避免stackoverflow,又不要因为担心stackoverflow而不敢写,大胆假设,小心求证。