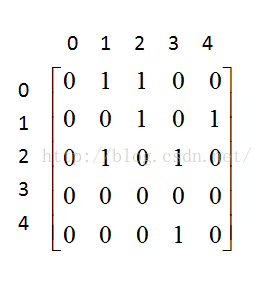java数据结构之图(邻接矩阵和邻接表)
JAVA数据结构之图
1、图的介绍和原理
1.1、图的基本概念
图是由顶点集(VertexSet)和边集(EdgeSet)组成,针对图G,顶点集和边集分别记为V(G)和E(G)。依据图的边集是否为有向,可把图分为有向图和无向图,根据图是否有权重,可以分为有权图和无权图。
图的基本术语:
1:邻接点----在一个无向图中,若存在一条边(Vi,Vj),则称Vi,Vj为此边的两个端点,并称它们互为邻接点;
2:出/入边 -----在一个有向图张,若存在一条边,则称此边为顶点Vi的出边,顶点Vj的一条入边;
3:度/入度/出度----无向图中的度定义为以该顶点为一个端点的边的数目,记为D(V)。有向图的入度定义为多少边指向该顶点,出度是该顶点出边的个数;
1.2、图的表示方式之邻接矩阵
图的表示方式有两种:二维数组表示(邻接矩阵);链表表示(邻接表)。
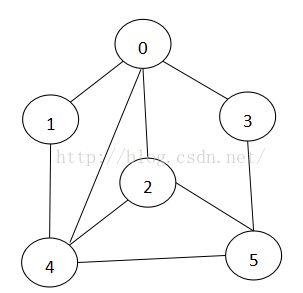
邻接矩阵是表示图形中顶点之间相邻关系的矩阵,对于n个顶点的图而言,矩阵是的row和col表示的是1....n个点。对于无向图 如果顶点b1和b2是连接的,那么在二维矩阵中matrix[b1,b2]和matrix[b2,b1]位置的值置为1,如果是有向图b1指向b2,那么 matrix[b1,b2]=1,matrix[b2,b1]=0;下面用一个例子表示无向图和有向图的邻接矩阵;
无向图
有向图
上面的无向图用邻接矩阵表示的话为: 该有向图用邻接矩阵来表示的话:
如果图是一个带权图,需要把1换为相应边上的权值,把非对角线上的换成一个很大的特定的实数则可,表示相应的边不存在,这个特定的实数通常用无穷大或MaxValue来表示,他要大于图G中所有边的权值(这里就不多加以举例)。
1.3、图的表示方式之邻接表
邻接矩阵与邻接表相比,它会造成空间的一定损失,它需要为每个顶点都分配n个边的空间,其实有很多边都是不存在边,但是邻接表的实现就不一样,它只关心存在的边,不关心不存在的边。邻接表由数组+链表组成对于上面的无向图,邻接表表示为(由于有向和无向的差别不是太大,所以只是画出了无向的邻接表表示):
该图标是为,标号为0的结点的相关联的结点为 1 2 3 4;标号为1的结点的相关联结点为0 4,标号为2的结点相关联的结点为 0 4 5......
2、图的实现
2.1、邻接矩阵表示图
package Graph;
//边集数组 ,存放边的信息
//邻域数组表示 和 邻域表表示 是两种不同的表示方式
//表示的是插入边的元素,边的起点和终点 边的权重
public class EdgeElement {
int fromvex;
int endvex;
int weight;
public EdgeElement(int v1,int v2){
//对于无权重图的初始化
fromvex=v1;
endvex=v2;
weight=1;
}
public EdgeElement(int v1,int v2,int wgt){
//对于有权重图的初始化
fromvex=v1;
endvex=v2;
weight=wgt;
}
}package Graph;
//可以通过边集来得到一个图的构成
public interface Graph {
void creatGraph(EdgeElement d[]); //通过边结点来构建一个图
GraphType graphType(); //返回图的类型 无向无权图 无向有权图 有向无权图 有向有权图 定义一个枚举变量
int vertices(); //返回图的顶点数
int edges(); //返回图的边数
boolean find(int i,int j); //从图中查找一条边(i,j)是否存在
void putEdge(EdgeElement theEdge); //像图中插入一条边 theEdge
void removeEdge(int i,int j); //从图中删除一条边
int degree(int i); //返回顶点i的度
int inDegree(int i); //返回顶点i的入度
int outDegree(int i); //返回顶点i的出度
void output(); //以图的顶点集和边集的形式输出一个图
void depthFirstSearch(int v); //从顶点v开始深度优先搜索整幅图
void breadthFirstSearch(int v); //从顶点v开始广度优先搜索整幅图
}
根据图的边集合创建一个图的邻接矩阵,图有四种类型,有向有权重、有向无权重、无向有权重、无向无权重。需要分为四种情况考虑。取出边结点的fromvex、endvex、weight信息,如果是无向无权重,那么a[fromvex][endvex]=a[endvex][fromvex]=1;如果是无向有权重,那么a[fromvex][endvex]=a[endvex][fromvex]=weight;如果是有向无权重,那么a[fromvex][endvex]=1;如果是有向有权重,那么a[fromvex][endvex]=weight;具体构造图的实现代码如下:
//在邻域数组中写数据
public void creatGraph(EdgeElement[] d) {
int i;
for(i=0;in-1 || v2<0 || v2>n-1 || v1==v2){
System.out.println("边的顶点序号无效,退出运行");
System.exit(0);
}
if(type==GraphType.NoDirectionNoWeight){
a[v1][v2]=a[v2][v1]=1;
}else if(type==GraphType.NoDirectionWeight){
a[v1][v2]=a[v2][v1]=d[i].weight;
}else if(type==GraphType.DirectionNoWeight){
a[v1][v2]=1;
}else{
a[v1][v2]=d[i].weight;
}
}
e=i; //边的数目
} public void putEdge(EdgeElement theEdge) {
int v1,v2;
v1=theEdge.fromvex;
v2=theEdge.endvex;
if(v1<0 || v1>n-1 || v2<0 || v2>n-1 || v1==v2){
System.out.println("边的顶点序号无效,退出运行!");
System.exit(0);
}
if(a[v1][v2]==0 || a[v1][v2]==MaxValue) e++; //边数e的值加一
if(type==GraphType.NoDirectionNoWeight || type==GraphType.NoDirectionWeight){
if(type==GraphType.NoDirectionNoWeight){
a[v1][v2]=a[v2][v1]=1;
}else{
a[v1][v2]=a[v2][v1]=theEdge.weight;
}
}else{
if(type==GraphType.DirectionNoWeight) a[v1][v2]=1;
else{
a[v1][v2]=theEdge.weight;
}
}
} public void removeEdge(int i, int j) {
if(i<0 || i>n-1 || j<0 || j>n-1 || i==j){
System.out.println("边的顶点序号无效,退出运行!");
System.exit(0);
}
if(a[i][j]==0 || a[i][j]==MaxValue){
System.out.println("要删除的边不存在,退出运行!");
System.exit(0);
}
if(type==GraphType.NoDirectionNoWeight){
a[i][j]=a[j][i]=0;
}else if(type==GraphType.NoDirectionWeight){
a[i][j]=a[j][i]=MaxValue;
}else if(type==GraphType.DirectionNoWeight){
a[i][j]=0;
}else a[i][j]=MaxValue;
e--;
} //得到该结点的度
public int degree(int i) {
if(i<0 || i> n-1){
System.out.println("参数的顶点序号值无效,退出运行");
System.exit(0);
}
int k=0;
if(type==GraphType.NoDirectionNoWeight || type==GraphType.NoDirectionWeight){
for(int j=0;j n-1){
System.out.println("参数的顶点序号值无效,退出运行");
System.exit(0);
}
if(type==GraphType.NoDirectionNoWeight || type==GraphType.NoDirectionWeight){
return -1;
}
int k=0;
for(int j=0;j n-1){
System.out.println("参数的顶点序号值无效,退出运行");
System.exit(0);
}
if(type==GraphType.NoDirectionNoWeight || type==GraphType.NoDirectionWeight){
return -1;
}
int k=0;
for(int j=0;j //输出
public void output() {
int i,j;
System.out.print("V={");//输出顶点集合
for(i=0;i");
}
}
}
}
}else{
for(i=0;i"+a[i][j]+",");
}
}
}
}
System.out.print("}");
} //深度优先进行搜索 是从哪个顶点开始遍历,这里可以用顶点序号表示顶点
public void depthFirstSearch(int v) { //驱动函数
boolean visited[]=new boolean[n];
for(int i=0;i***************************************分割线*********************
2.2邻接表表示图(由于实现起来只是不太难的逻辑,所以代码不做太多解释)
邻接表结点定义,存储指向的结点,该结点的权重,还有该节点指向的下一个结点,具体代码实现如下:
package GraphLink;
//定义邻接表类型
public class EdgeNode{
//需要一个存储自身结点
int adjvex;
int weight;
EdgeNode next;
//无权图
public EdgeNode(int adj,EdgeNode nt){
this.adjvex=adj;
this.next=nt;
this.weight=1;
}
//有权图
public EdgeNode(int adj,int wgt,EdgeNode nt){
this.adjvex=adj;
this.weight=wgt;
this.next=nt;
}
}
通过边集合生成一个邻接表代码如下:
//生成图函数
@Override
public void creatGraph(EdgeElement[] d) {
int i;
for(i=0;in-1||v2<0||v2>n-1||v1==v2){
System.out.println("边的顶点序号无效,退出运行");
System.exit(0);
}
if(type==GraphType.NoDirectionNoWeight){//处理无方向 无权重的图
a[v1]=new EdgeNode(v2,a[v1]);//把边挂载在主干上,a为EdgeNode类型的一维数组
a[v2]=new EdgeNode(v1,a[v2]);//处理第二条边
}else if(type==GraphType.NoDirectionWeight){//处理无向有权图
a[v1]=new EdgeNode(v2,weight,a[v1]);
a[v2]=new EdgeNode(v1,weight,a[v2]);
}else if(type==GraphType.DirectionNoWeight){//处理有向无权图
a[v1]=new EdgeNode(v2,a[v1]);
}else {
a[v1]=new EdgeNode(v2,weight,a[v1]);
}
}
e=i;
} //在图中查找一条边
public boolean find(int v1,int v2){
if(v1<0||v1>n-1||v2<0||v2>n-1||v1==v2){
System.out.println("边的顶点序号无效,退出运行");
System.exit(0);
}
EdgeNode p=a[v1];
while(p!=null){
if(p.adjvex==v2){
return true;
}
p=p.next;
}
return false;
} //向图中插入一条边
public void putEdge(EdgeElement theEdge){
int v1,v2,weight;
v1=theEdge.fromvex;
v2=theEdge.endvex;
weight=theEdge.weight;
if(v1<0||v1>n-1||v2<0||v2>n-1||v1==v2){
System.out.println("边的顶点序号无效,退出运行");
System.exit(0);
}
EdgeNode p=a[v1];
while(p!=null){
if(p.adjvex==v2){
break;//退出后处理
}
p=p.next;
}
if(p==null) e++;
else{
if(type==GraphType.DirectionWeight || type==GraphType.NoDirectionWeight){
p.weight=weight;
}
if(type==GraphType.NoDirectionWeight){//无向有权重的另一条边也要处理
EdgeNode q=a[v2];
while(q!=null){
if(q.adjvex==v1) break;
q=q.next;
}
q.weight=weight;
}
return;
}
if(type==GraphType.NoDirectionNoWeight){//如果是无向无权重
a[v1]=new EdgeNode(v2, a[v1]);
a[v2]=new EdgeNode(v1, a[v2]);
}else if(type==GraphType.NoDirectionWeight){//处理无向有权重
a[v1]=new EdgeNode(v2,weight,a[v1]);
a[v2]=new EdgeNode(v1,weight,a[v2]);
}else if(type==GraphType.DirectionNoWeight){//有向无权重
a[v1]=new EdgeNode(v2,a[v1]);
}else{
a[v1]=new EdgeNode(v2, weight,a[v1]);
}
} public void removeEdge(int v1,int v2){
if(v1<0||v1>n-1||v2<0||v2>n-1||v1==v2){
System.out.println("边的顶点序号无效,退出运行");
System.exit(0);
}
EdgeNode p=a[v1],q=null;//拿到主干结点
while(p!=null){
if(p.adjvex==v2) break;
q=p;
p=p.next;
}
if(p==null){
System.out.println("要删除的边不存在,程序退出运行");
System.exit(0);
}
if(q==null){//该结点在表头上 主干的节点就是需要找的结点
a[v1]=a[v1].next;
}else{
q.next=p.next;//嫁接上
}
//删除无向图的另一个结点上的边
if(type==GraphType.NoDirectionNoWeight||type==GraphType.NoDirectionWeight){
EdgeNode p1=a[v2],q1=null;
while(p1!=null){
if(p1.adjvex==v1){
break;
}
q1=p1;
p1=p1.next;
}
if(q1==null){
a[v2]=a[v2].next;
}else{
q1.next=p1.next;
}
}
e--;
} //返回一个顶点的度,度分为入度和出度,要分别处理
public int degree(int i){
if(i<0||i>n-1){
System.out.println("顶点超过了范围,程序退出运行");
System.exit(0);
}
int k=0;
if(type==GraphType.NoDirectionNoWeight||type==GraphType.NoDirectionWeight){
EdgeNode p=a[i];
while(p!=null){
k++;
p=p.next;
}
return k;
}else return inDegree(i)+outDegree(i);
}
//求出并返回一个顶点的入度
public int inDegree(int i){//返回指向该顶点的度,入度,用双循环来实现
int k=0;//记录入度个数
if(i<0||i>n-1){
System.out.println("顶点超过了范围,程序退出运行");
System.exit(0);
}
if(type==GraphType.NoDirectionNoWeight||type==GraphType.NoDirectionWeight){
return -1;
}else{
for(int j=0;j //得到邻接矩阵
public int[][] getAdjacencyMatrix(){
int adjacencyMatrix[][]=new int[n][n];
if(type==GraphType.DirectionNoWeight||type==GraphType.DirectionWeight){//有向性
//有向 那不存在的边是存在一个InfinityValue
for(int i=0;i
由于我想实现的逻辑是可以增加或者删除一个图中的任意顶点,上面的结构实现删除一个顶点稍微有点困难,目前还在修改代码中,但是发出来的函数都是通过案例测试过,功能实现没任何问题,可放心使用。
该工程文件我已经传到github上,上传的工程里面涵盖数据结构大部分结构:链表、线性表、堆栈、队列、二叉树、图、堆、查找、搜索。里面有详细的实现步骤,有需要可以下载。github地址:https://github.com/xxniuren/JAVA-DataStructure.git