A Spy in the Metro

Description

Secret agent Maria was sent to Algorithms City to carry out an especially dangerous mission. After several thrilling events we find her in the first station of Algorithms City Metro, examining the time table. The Algorithms City Metro consists of a single line with trains running both ways, so its time table is not complicated.

Maria has an appointment with a local spy at the last station of Algorithms City Metro. Maria knows that a powerful organization is after her. She also knows that while waiting at a station, she is at great risk of being caught. To hide in a running train is much safer, so she decides to stay in running trains as much as possible, even if this means traveling backward and forward. Maria needs to know a schedule with minimal waiting time at the stations that gets her to the last station in time for her appointment. You must write a program that finds the total waiting time in a best schedule for Maria.

The Algorithms City Metro system has N stations, consecutively numbered from 1 to N. Trains move in both directions: from the first station to the last station and from the last station back to the first station. The time required for a train to travel between two consecutive stations is fixed since all trains move at the same speed. Trains make a very short stop at each station, which you can ignore for simplicity. Since she is a very fast agent, Maria can always change trains at a station even if the trains involved stop in that station at the same time.

Input

The input file contains several test cases. Each test case consists of seven lines with information as follows.

Line 1.

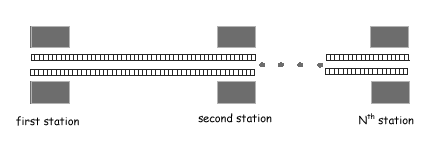
The integer N ( 2N50), which is the number of stations.

Line 2.

The integer T ( 0T200), which is the time of the appointment.

Line 3.

N - 1 integers: t₁, t₂,..., t_{N - 1} ( 1t_i70), representing the travel times for the trains between two consecutive stations: t₁ represents the travel time between the first two stations, t₂ the time between the second and the third station, and so on.

Line 4.

The integer M1 ( 1M150), representing the number of trains departing from the first station.

Line 5.

M1 integers: d₁, d₂,..., d_M1 ( 0d_i250 and d_i < d_{i + 1}), representing the times at which trains depart from the first station.

Line 6.

The integer M2 ( 1M250), representing the number of trains departing from the N-th station.

Line 7.

M2 integers: e₁, e₂,..., e_M2 ( 0e_i250 and e_i < e_{i + 1}) representing the times at which trains depart from the N-th station.

The last case is followed by a line containing a single zero.

Output

For each test case, print a line containing the case number (starting with 1) and an integer representing the total waiting time in the stations for a best schedule, or the word ` impossible' in case Maria is unable to make the appointment. Use the format of the sample output.

Sample Input

4
55
5 10 15
4
0 5 10 20
4
0 5 10 15
4
18
1 2 3
5
0 3 6 10 12
6
0 3 5 7 12 15
2
30
20
1
20
7
1 3 5 7 11 13 17
0

Sample Output

Case Number 1: 5
Case Number 2: 0
Case Number 3: impossible

题意：是说一个间谍需要T时间到达最后一个车站；可以再某一个车站停留；但是为了减小风险；停留的时间越小越小越好；

数据中：第一个数是车站数，第二行为时间；第三行代表有多少趟车从第一个车站开往最后一个车站；接下来的一行是车子从第一个车站出发的时间;第五行是代表又多少辆车从最后一站开往第一站;接下来的一行是发车时间；可以知道是一道dp题;

# include 
# include 
# include 
# include 
using namespace std;

const int INF=100000000;

//has_train[ t ] [ i] [ 0 ]代表是在t时刻第 i 个车站有车子往右开；
int main()
{
    int n,kcase=0;
    while(cin>>n&&n)
    {
        int T,t[55],i,j,has_train[205][55][2],dp[205][55],M1,M2,d;
        cin>>T;
        for(i=1;i>t[i];    //储存每两个车站之间的距离;
        memset(has_train,0,sizeof(has_train));
        cin>>M1;
        while(M1--)
        {
            cin>>d;
            for(j=1;j>M2;
        while(M2--)
        {
            cin>>d;
            for(j=n-1;j>=1;j--)
            {
                if(d<=T) has_train[d][j+1][1]=1;
                d+=t[j];
            }
        }

        // dp [ i][j ]的意义：在 t 时刻到达第j个车站还需要等待的时间;
        for(i=1;i=0;i--)
        {
            for(j=1;j<=n;j++)
            {
                dp[i][j]=dp[i+1][j]+1;
                if(j1&&has_train[i][j][1]&&i+t[j-1]<=T)  //同上;
                    dp[i][j]=min(dp[i][j],dp[i+t[j-1]][j-1]);
            }
        }
        cout<<"Case Number "<<++kcase<<": ";
        if(dp[0][1]>=INF)    cout<<"impossible"<