牛客多校9 - Groundhog Chasing Death(质因子分解+思维)

题目链接：点击查看

题目大意：给出 a , b , c , d , x , y ，求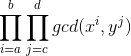

题目分析：因为涉及到了 gcd 的乘积运算，那么易知不同质因子的贡献是相互独立的，首先我们就可以先将 x 和 y 进行质因子分解，那么对于质因子 p 来说，设 cntx[ p ] 为 p 在 x 中出现的次数，cnty[ p ] 为 p 在 y 中出现的次数，不难看出，需要这两个数同时大于 0 才有贡献，如果其中一者为 0 的话，那么其表示的质因子就是 p^0 = 1 ，gcd 求出来显然也就是 1 了，对答案没有贡献

到此，cntx[ p ] 和 cnty[ p ] 都大于 0 ，那么质因子 p 的 gcd 就是 ，也就是 ，这也就提醒我们可以对指数单独处理，最后求一下 p 的幂次再乘起来就是答案了

此时我们可以对指数稍微打表找一下规律，打表程序如下（可以自己更改一下 i 和 j 的取值范围，分别代表 [ a , b ] 和 [ c , d ] ）：

for(int k=1;k<=5;k++)//质因子p在x中的个数 
	for(int t=1;t<=5;t++)//质因子p在y中的个数 
	{
		printf("*****cntx:%d cnty:%d*****\n",k,t);
		for(int i=1;i<=5;i++)//a~b
		{
			for(int j=1;j<=5;j++)//c~d 
				printf("%d ",min(i*k,j*t));
			puts("");
		}
	}

这里不卖关子了，直接说规律：

1. 当 i 确定时，[ c , d ] 的一列可以分为两段：
   1. 前半段为等差数列
   2. 后半段为常数
2. 当 j 确定时，[ a , b ] 的一行可以分为两段：
   1. 前半段为等差数列
   2. 后半段为常数

这样就可以将 ( b - a + 1 ) * ( d - c + 1 ) 的时间复杂度优化为 ( b - a + 1 ) 或者 ( d - c + 1 ) 了，因为知道了是等差数列，我们可以求出三项：第一项，第二项，最后一项，根据第一项和第二项得出公差，根据第一项、最后一项和公差计算出等差数列的长度，这样最后常数项的长度也能计算得出了

有个小坑就是，如果指数直接进行运算的话，会爆 long long ，可以用费马小定理降幂，一方面是保证指数在数据范围内，另一方面是加速快速幂的运算

因为我用了 map 参与质因子分解，所以总的时间复杂度为 ( b - a + 1 ) * logn * logn

代码：
 

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include