图论模型笔记

图论问题对应的解决模型

图论问题	解决模型
最短路问题	Dijkstra 算法 和 Floyed 算法
公路连接问题	Prim 算法 和 Kruskal 算法
指派问题	匈牙利算法、KM 算法
中国邮递员问题	Fleury 算法
旅行商问题	蚁群算法、遗传算法、模拟退火
运输问题	表上作业法

最短路问题（Dijkstra 算法 和 Floyed 算法）

① 适用范围
适用于两个指定顶点间的最短路问题（Dijkstra）和任意两对顶点间的最短路问题（Floyed），前者可解决无负权值和无负环的路径问题，后者可解决有负权值和无负环的路径问题，并且两者都可以解决有向图和无向图，由于有负环的路径问题很少出现，因此暂不考虑 Bellman_Ford 算法

② 如何排版
具体步骤和相关模型模板可在 图与网络 $\S 3$应用—最短路问题 中查阅

③ 路径图片
Ⅰ、可以选择 Graph Editor（手动作图）

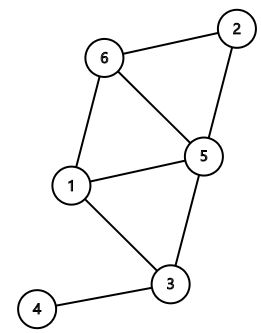
Ⅱ、也可以选择 MATLAB 自带的画图函数

MATLAB 作图代码

s = [1,2,3,4,1];		//起始点
t = [2,3,1,1,4];		//到达点
w = [3,8,9,2,6];		//权重 （可选择不加）
G = digraph(s, t, w);	//digraph  为有向图     graph 为无向图
% plot(G, 'linewidth', 2)  //仅无权图使用   第三个参数是线的宽度
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 	 //仅有权图使用
set( gca, 'XTick', [], 'YTick', [] );  		//不显示坐标

④ Dijkstra – C++ 代码
以指定两顶点间的最短路径，输出带路径的最小费用 演示

#include 
#define INF (int)1e18
#define pii pair 
#define mp(a, b) make_pair(a, b)
using namespace std;
int pre[100000];	//记录前驱 
int p,len,tim[100000];	//输出前驱 
int head[100000],cnt;
long long ans[1000000];
bool vis[1000000];
int m,n,s,u;
struct node
{
    int to;
    int wei;
    int nextt;
}edge[1000000];
struct cmp
{
    bool operator()(const pii p1, const pii p2)
    {
        return p1.first > p2.first; // first的小值优先 
    }
};
void addedge(int x,int y,int z)
{
	pre[y]=x;	//记录前驱 
    edge[++cnt].to=y;
    edge[cnt].wei=z;
    edge[cnt].nextt=head[x];
    head[x]=cnt;
}
priority_queue <int,vector<pii>,cmp > q;
int main()
{
    cin>>n>>m>>s>>p;	//点数 边数 出发点 目标点
    for(int i=1;i<=n;i++)
        ans[i]=INF;
    ans[s]=0;
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        addedge(a,b,c);
        //addedge(b,a,c);  //若目标图是无向图
    }
    q.push(mp(0,s));
    while(!q.empty())
    {
        pii temp=q.top();
        q.pop();
        u=temp.second;
        if(!vis[u])
        {
            vis[u]=1;
            for(int i=head[u];i;i=edge[i].nextt)
            {
                int v=edge[i].to;
                if(ans[v]>ans[u]+edge[i].wei)
                {
                    ans[v]=ans[u]+edge[i].wei;
                    pre[v]=u;	//记录前驱 
                    if(!vis[v])
                    {
                        q.push(mp(ans[v],v));
                    }
                }
            }
        }
    }
    printf("对应的最短距离为：%d\n",ans[p]);
    while(p!=0)
    {
        tim[len++] = p;
        p = pre[p];
    }
    printf("路径为：");
    for(int i=len-1;i>0;i--)
        printf("%d->",tim[i]);
    printf("%d",tim[0]);
    return 0;
}

input:
9 16 1 8
1 2 6
1 4 1
1 3 3
3 2 2
3 4 2
2 5 1
5 4 6
4 6 10
5 6 4
6 5 10
6 7 2
5 7 3
5 8 6
7 8 4
9 5 2
9 8 3

output:
对应的最短距离为：12
路径为：1->3->2->5->8

⑤ Floyed – C++ 代码
以指定任意两对顶点间的最短路径，输出最小费用 演示

#include
#define INF (short int)1e18
using namespace std;
int a[20005][20005],n,m,s;
inline void floyd()
{
    for(int k=1;k<=n;k++) //这里要先枚举 k（可以理解为中转点）
	{
        for(int i=1;i<=n;i++)
		{
            if(i==k||a[i][k]==INF) //若该点是中转点 或 要到的地方是中转点
                continue;
			for(int j=1;j<=n;j++)
				a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
        }
    }
}
int main()
{
	cin>>n>>m;	  //点数 边数
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i!=j) a[i][j]=INF;
    for(int i=1,u,v,w;i<=m;i++)
	{
		cin>>u>>v>>w;
        a[u][v]=min(a[u][v],w);
		//a[v][u]=min(a[v][u],w); //若目标图是无向图 
    }
    floyd();
    while(~scanf("%d %d",&n,&m))	//输入路径（升序输入） 
    	printf("%d\n",a[n][m]); 
    return 0;
}
input:
9 16
1 2 6
1 4 1
1 3 3
3 2 2
3 4 2
2 5 1
5 4 6
4 6 10
5 6 4
6 5 10
6 7 2
5 7 3
5 8 6
7 8 4
9 5 2
9 8 3

input:
1 8
output:
12
input:
1 5
output:
6

公路连接问题（Prim 算法 和 Kruskal 算法）

① 适用范围
适用于边比较多的最小生成树问题（Prim）和点比较多的最小生成树问题（Kruskal），前者可解决稠密图的路径问题，后者可解决稀疏图的路径问题，但不擅长解决无向图，两者都可以将所有点以最小的权值连接

② 如何排版
具体步骤和相关模型模板可在 图与网络 $\S 4$树 中查阅

③ 路径图片
适合选用 MATLAB 自带的画图函数

MATLAB 作图代码

W = [.41 .29 .51 .32 .50 .45 .38 .32 .36 .29 .21];	 //权重
DG = sparse([1 1 2 2 3 4 4 5 5 6 6],[2 6 3 5 4 1 6 3 4 2 5],W);	 //起始点 和 到达点
UG = tril(DG + DG');	 //生成树
view(biograph(UG,[],'ShowArrows','off','ShowWeights','on'))	 //画出树
[ST,pred] = graphminspantree(UG)  //最小生成树
view(biograph(ST,[],'ShowArrows','off','ShowWeights','on'))  //画出最小生成树

④ Prim – C++ 代码
以输出稠密图的最小费用 演示

#include
using namespace std;
const int maxn = 5005;
const int maxm = 200005;
int head[maxn],cnt;
int s[maxn];
inline int read() {
  int x = 0, neg = 1; char op = getchar();
  while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); }
  while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); }
  return neg * x;
}
struct node{
    int to;
    int nextt;
	int wei;
    friend bool operator < (node a,node b)
    {
        return a.wei > b.wei;
    }
}edge[maxm<<1];
inline void add(int x,int y,int z)
{
    edge[++cnt].to = y;
    edge[cnt].wei = z;
    edge[cnt].nextt = head[x];
    head[x] = cnt;
}
priority_queue<node> q;
inline int prim(int u0,int n)
{
    int res = 0;
    s[u0] = 1;
    for(register int i = head[u0];i;i = edge[i].nextt)
        q.push(edge[i]);
    for(register int i = 1;i < n;i++)
    {
        if(!q.size())break;
        node now = q.top();
        q.pop();
        if(s[now.to])
        {
            while(s[now.to])
            {
                now = q.top();
                q.pop();
            }
        }
        res += now.wei;
        s[now.to] = 1;
        for(register int j = head[now.to];j;j = edge[j].nextt)
        {
            if(!s[edge[j].to])q.push(edge[j]);
        }
    }
    return res;
}
int main()
{
    int n,m,a,b,x;
    n=read(),m=read();		//点数 边数 
    for(register int i = 1;i <= m;i++)
	{
		a=read(),b=read(),x=read();
        add(a,b,x);
        //add(b,a,x); //若目标图是无向图 
    }
    printf("%d\n",prim(1,n));
    return 0;
}

input:
4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

output:
7

⑤ Kruskal – C++ 代码
以输出稀疏图的最小费用 演示

#include 
using namespace std;
const int N = 1005;
const int MAXN = 10005;
int father[N];
int n, m;
struct Edge
{
    int u;
    int v;
    int w;
    bool operator < (const Edge &b)const
    {
    	return w<b.w;
    }
}e[MAXN];  
inline Find(int x)
{
    if(x != father[x])
    	father[x] = Find(father[x]);
    return father[x]; 
}
inline int Merge(int a, int b) //并查集
{
    int p = Find(a);
    int q = Find(b);
    if(p==q) return 0;
    if(p > q)
        father[p] = q;
    else
        father[q] = p;
    return 1;
}
int Kruskal(int n,int m)
{
    int ans = 0,nn = n;
    for(int i=1;i<=m;i++)
        if(Merge(e[i].u, e[i].v)) //判断是否成环 
        {
            ans += e[i].w;
            nn--;
            if(nn==1)
                return ans;
        }
    return 0;
}
int main() 
{
    cout <<"输入结点数n和边数m："<<endl;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        father[i] = i;
    cout <<"输入结点数u，v和边值w："<<endl;
    for(int i=1;i<=m;i++)
        cin>>e[i].u>>e[i].v>>e[i].w;
    sort(e+1, e+m+1);
    int ans = Kruskal(n,m);
    cout << "最小的花费是：" << ans << endl;
    return 0;
}

input:
4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

output:
7

指派问题（匈牙利算法 和 KM 算法）

① 适用范围
适用于在多项式时间内求解任务分配问题（匈牙利算法）和前者加上最大权值的问题（KM），后者仅适用于完全匹配问题

② 如何排版
具体步骤和相关模型模板可在 图与网络 $\S 5$匹配问题 中查阅

③ 路径图片
查阅文献和论文选取图片

④ 匈牙利算法 – C++ 代码

#include 
#define IO std::ios::sync_with_stdio(false)
#define clr(a, b) memset((a), (b), sizeof(a))
using namespace std;
const int maxn=1e3; 
int t,u,v,n,m;
int line[maxn][maxn],used[maxn],nxt[maxn];
bool Find(int x)
{
	for(int y=1;y<=m;i++)
	{
		if(line[y][i]&&!used[y])
		{
			used[y]=1;
			if(nxt[y]==0||Find(nxt[y]))
			{
				nxt[y]=x;
				return true;
			}
		}
	}
	return false;
}
int match()
{
	int sum=0;
	for(int x=1;x<=n;x++)
	{
		clr(used,0);
		if(Find(x)) sum++;
	}
	return sum;
}

int main()
{
	IO;
	cin>>t>>n>>m;	// t 组数据     左集合 n 个元素   右集合 m 个元素
	while(t--)
	{
		cin>>u>>v;
		line[u][v]=1;
	}
	cout<<match()<<endl;		//能匹配到的最大个数
	return 0;
}

⑤ KM 算法 – C++ 代码

#include 
#define INF (int)1e18
#define IO std::ios::sync_with_stdio(false)
#define clr(a, b) memset((a), (b), sizeof(a))
using namespace std;
const int maxn = 305;
int n,nx,ny,sum;
int line[maxn][maxn],nxt[maxn],slack[maxn];
int lx[maxn],ly[maxn];
bool visx[maxn],visy[maxn];

bool Find(int x)
{
    int d;
    visx[x] = true;
    for(int y = 1 ; y <= ny ; ++y)
	{
        if(visy[y]) continue;
        d = lx[x] + ly[y] - line[x][y];
        if(d == 0)
		{
            visy[y] = true;
            if(nxt[y] == 0 || Find(nxt[y]))
			{
                nxt[y] = x;
                return true;
            }
        }
        else if(slack[y] > d)
            slack[y] = d;
    }
    return false;
}
void KM()
{
    for(int x = 1 ; x <= nx ; ++x)
	{
        for(int i = 1 ; i <= ny ; i++) slack[i] = INF;
        while(1)
		{
            clr(visx,false);
            clr(visy,false);
            if(Find(x)) break;
            else
			{
                int d = INF;
                for(int i = 1 ; i <= ny ; i++)
                    if(!visy[i] && d > slack[i])
                        d = slack[i];
                for(int i = 1 ; i <= nx ; i++)
                    if(visx[i]) lx[i] -= d;
                for(int i = 1 ; i<= ny ; i++)
				{
                    if(visy[i])
                        ly[i] += d;
                    else
                        slack[i] -= d;
                }
            }
        }
    }
}
int main()
{
	IO;
    while(scanf("%d",&n) != EOF)		//输入 n 组数据
	{
        nx = ny = n;
        for(int i = 1 ; i <= nx ; ++i)
            for(int j = 1 ; j <= ny ; ++j)
                scanf("%d",&line[i][j]);		//输入 n 组 每次左右集合的值
        clr(nxt,0);
		clr(ly,0);
	    for(int i = 1 ; i <= nx ; ++i)
		{
	         lx[i] = -INF;
	         for(int j = 1 ; j <= ny ; ++j)
	             if(lx[i] < line[i][j])
	                 lx[i] = line[i][j];
	    }
	    KM();
        sum = 0;
        for(int i = 1 ; i <= ny ; ++i)
            if(nxt[i] != -1)
                sum += line[nxt[i]][i];
        printf("%d\n",sum);			//最大权值
    }
    return 0;
}

中国邮递员问题（Fleury 算法）

① 背景介绍

1）欧拉图： 存在经过图中每条边恰好一次并且仅一次行遍所有点的回路

• 通俗来说，该回路有两个特点：
  • 边：包括图中所有边（不重复地）
  • 点：包括图中所有点（可重复地）

2）欧拉图判断： 不存在奇度顶点

• 通俗来说，图中每个顶点与偶数条边相连

3）欧拉回路求解： 判断一个图是欧拉图，下一步就会问这条回路具体是什么，Fleury算法就是用来找出无向欧拉图可能的的欧拉回路

4）中国邮递员问题： 综上，该问题就是求欧拉图的回路

② 如何排版
具体步骤和相关模型模板可在 图与网络 $\S 6.3.1$邮递员问题 中查阅

③ 路径图片
查阅文献和论文选取图片

④ 如何求解
中国邮递员问题的深入剖析与算法实现(附例题及MATLAB、LINGO代码)
等一系列代码，网上可以搜寻

旅行商问题（蚁群算法、遗传算法）

① 背景介绍

1）哈密顿图： 存在经过图中每条边和点恰好一次并且仅一次行遍所有点的回路

• 通俗来说，该回路有两个特点：
  • 边：包括图中所有边（不重复地）
  • 点：包括图中所有点（不重复地）

2）旅行商问题： 综上，该问题就是求哈密顿图的回路

② 如何排版
具体步骤和相关模型模板可在 图与网络 $\S 6.3.2$旅行商（TSP）问题 中查阅

③ 路径图片
查阅文献和论文选取图片

④ 如何求解
用到到蒙特卡洛模型，蚁群算法、遗传算法、模拟退火等一系列智能算法

运输问题 （表上作业法）

一类具有特殊结构的线性规划问题，需要用到 lingo 等软件