Lingo 基础+实战
Lingo 基础知识
大佬博客(看这个就够了)
Lingo 实战一:(线性规划)
| 变量 | 含义 |
|---|---|
| ( a i , b i ) (a_i,b_i) (ai,bi) | 工地 i i i 的坐标( i i i = 1…6) |
| ( x i , y i ) (x_i,y_i) (xi,yi) | 料场 j j j 的坐标( j j j = 1,2) |
| c i j c_{i j} cij | 从料场 j j j 往工地 i i i 运输的水泥量 (所求) |
| z z z | 最小的吨千米数 (所求) |
| d i d_i di | 第 i i i 个工厂的日需求量 |
| e j e_j ej | 第 j j j 个料场的总供应量 |
约束方程如下:
min z = ∑ j = 1 2 ∑ i = 1 6 c i j ( x j − a i ) 2 + ( y j − b i ) 2 \min z=\sum_{j=1}^{2} \sum_{i=1}^{6} c_{i j} \sqrt{\left(x_{j}-a_{i}\right)^{2}+\left(y_{j}-b_{i}\right)^{2}} minz=j=1∑2i=1∑6cij(xj−ai)2+(yj−bi)2
s . t { ∑ j = 1 2 c i j = d i , i = 1 , 2 , … , 6 ∑ i = 1 6 c i j ≤ e j , j = 1 , 2 s.t\left\{\begin{array}{l} \sum_{j=1}^{2} c_{i j}=d_{i}, i=1,2, \ldots, 6 \\ \sum_{i=1}^{6} c_{i j} \leq e_{j}, j=1,2 \end{array}\right. s.t{∑j=12cij=di,i=1,2,…,6∑i=16cij≤ej,j=1,2
Lingo 代码:
!集合的定义
sets:
S/1..6/:a,b,d;
T/1..2/:e,x,y;
U(S,T):c;
endsets
!已知的数据段
data:
a=1.25 8.75 0.5 5.75 3 7.25;
b=1.25 0.75 4.75 5 6.5 7.75;
d=3 5 4 7 6 11;
x=5 2;
y=1 7;
e=20 20;
enddata
!模型的式子
min = @sum(U(i,j):c(i,j)*((x(j)-a(i))^2+(y(j)-b(i))^2)^(1/2));
@for(S(i):@sum(T(j):c(i,j))=d(i));
@for(T(j):@sum(S(i):c(i,j))<=e(j));
结果如下:

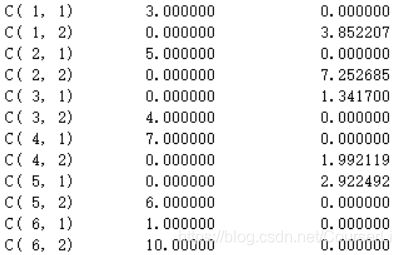
用 Lingo 求解为:
A 料场向工地1运送3吨,向工地2运送5吨,向工地3运送0吨,向工地4运送7吨,向工地5运送0吨,向工地6运送1吨
B 料场向工地1运送0吨,向工地2运送0吨,向工地3运送4吨,向工地4运送0吨,向工地5运送6吨,向工地6运送10吨
局部最优解为136.228
Lingo 实战二:(多目标规划)
| 变量 | 含义 |
|---|---|
| x 1 x_1 x1 | 工厂每个月生产产品 A A A 吨数 |
| x 2 x_2 x2 | 工厂每个月生产产品 B B B 吨数 |
约束方程如下:
{ min f 1 = 2 x 1 + 5 x 2 min f 2 = 0.4 x 1 + 0.3 x 2 st. { x 1 + x 2 ≥ 7 0 ≤ x 1 ≤ 5 0 ≤ x 2 ≤ 6 \left\{\begin{array}{l} \min f_{1}=2 x_{1}+5 x_{2} \\ \min f_{2}=0.4 x_{1}+0.3 x_{2} \\ \text { st. }\left\{\begin{array}{l} x_{1}+x_{2} \geq 7 \\ 0 \leq x_{1} \leq 5 \\ 0 \leq x_{2} \leq 6 \end{array}\right. \end{array}\right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧minf1=2x1+5x2minf2=0.4x1+0.3x2 st. ⎩⎨⎧x1+x2≥70≤x1≤50≤x2≤6
多目标规划 转换为 单目标规划:
下面我们将其转换为一个单目标规划问题,即对上面的两个目标函数进行加权。由于该工厂决策认为环境污染应优先考虑,因此我们可以选取 f 1 f_1 f1 和 f 2 f_2 f2 的权重分别为 0.4 和 0.6,注意到两个目标函数的单位不同,一个为"万元",一个为“吨”,因此我们需要首先对目标函数进行标准化来消除量纲的影响,然后再进行加权。由于题目中已经给了产品费用和污染量的参考值,因此我们将这两个目标函数分别除以其参考值来消除量纲。那么加权组合后的目标函数:
m i n f = 0.4 × f 1 30 + 0.6 × f 2 2 = 0.4 30 × ( 2 x 1 + 5 x 2 ) + 0.6 2 × ( 0.4 x 1 + 0.3 x 2 ) min\;f=0.4 \times \frac{f_{1}}{30}+0.6 \times \frac{f_{2}}{2}=\frac{0.4}{30} \times\left(2 x_{1}+5 x_{2}\right)+\frac{0.6}{2} \times\left(0.4 x_{1}+0.3 x_{2}\right) minf=0.4×30f1+0.6×2f2=300.4×(2x1+5x2)+20.6×(0.4x1+0.3x2)
Lingo 代码:
!模型的式子
min = 0.4/30*(2*x1+5*x2)+0.6/2*(0.4*x1+0.3*x2);
x1+x2>7;
0<=x1;
x1<=5;
0<=x2;
x2<=6;
结果如下:
x 1 = 5 , x 2 = 2 , f 1 = 20 , f 2 = 2.6 x_{1}=5, \quad x_{2}=2, \quad f_{1}=20, \quad f_{2}=2.6 x1=5,x2=2,f1=20,f2=2.6
Lingo 其他知识
一、灵敏度分析
先在 Lingo 菜单 options 里面设置 general solver 的 dual computation 里面加上 ranges,
然后在 Lingo 菜单里面选 range 就行了(注意 Lingo 只能对线性的模型做灵敏度分析)
灵敏度分析报告