最小生成树模板 洛谷 Prim算法和Kruskal算法
洛谷-最小生成树模板
题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。
输入格式
第一行包含两个整数 N,M,表示该图共有 N 个结点和 M 条无向边。
接下来 MM 行每行包含三个整数 Xi,Yi,Zi ,表示有一条长度为 Zi 的无向边连接结点 Xi,Yi。
输出格式
如果该图连通,则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。
输入输出样例
输入
4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3输出
7最小生成树MST有两种基本的算法:Kruskal算法和Prim算法。
首先介绍Kruskal算法:
它的基本思想为:将所有边按照权值的大小进行升序排序,然后从小到大一一判断,条件为:如果这个边不会与之前选择的所有边组成回路,就可以作为最小生成树的一部分;反之,舍去。直到具有 n 个顶点的连通网筛选出来 n-1 条边为止。筛选出来的边和所有的顶点构成此连通网的最小生成树。
要使最小生成树边权值之和最小,树的每一条边权值应尽量小。因此,有以下几个步骤:
假设连通网N=(V,{E}),T=(V,{TE})表示N的最小生成树,TE为最小生成树上边的集合。初始时令TE为空集。
Step1:令最小生成树T的初态为只有n个顶点的非连通图T=(V,{TE}),TE={}。
Step2:从权值最小的边(u,v)开始,若该边依附的两个顶点落在T的不同连通分量上,则将此边加入到TE中,即TE=TE∪(u,v),否则舍弃此边,选择下一条代价最小的边。
Step3:重复Step2,直至TE所有顶点在同一连通分量上。此时T=(V,{TE})就是N的一棵最小生成树。
判断是否有回路则使用到了并查集的概念。
并查集主要用来解决判断两个元素是否属于同一个集合,以及把两个集合合并的一种数据结构。并查集初始时把每一个对象看作是一个单元素集合;然后依次按顺序读入等价对后,将等价对中的两个元素所在的集合合并。在此过程中将重复地使用一个搜索(find)运算,确定一个元素在哪一个集合中。当读入一个等价对A≡B时,先检测A和B是否同属一个集合,如果是,则不用合并;如果不是,则用一个合并(union)运算把A、B所在的集合合并,使这两个集合中的任两个元素都是等价的。因此,并查集在处理时主要有搜索和合并两个运算。
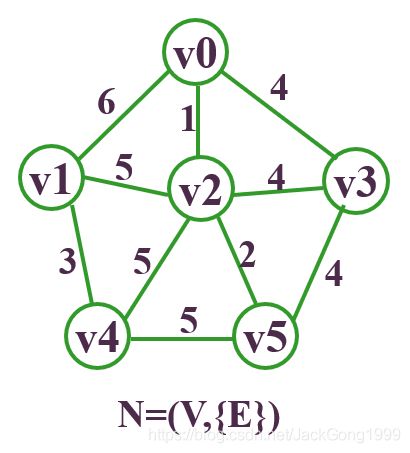
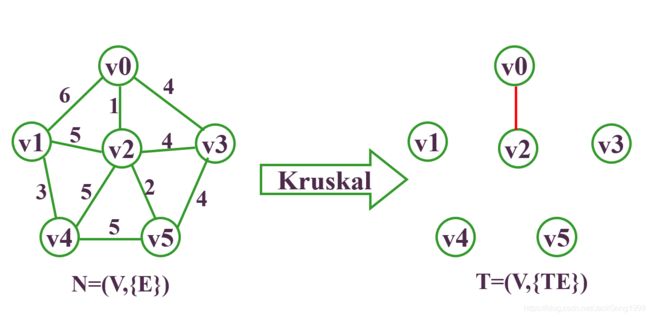
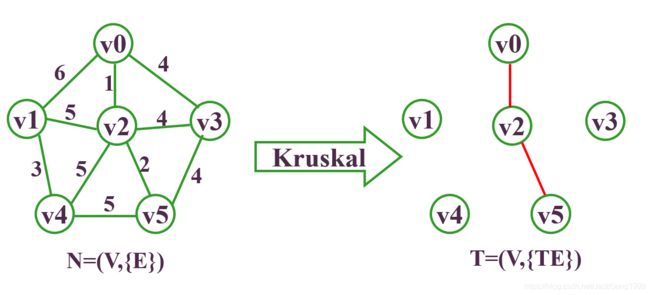
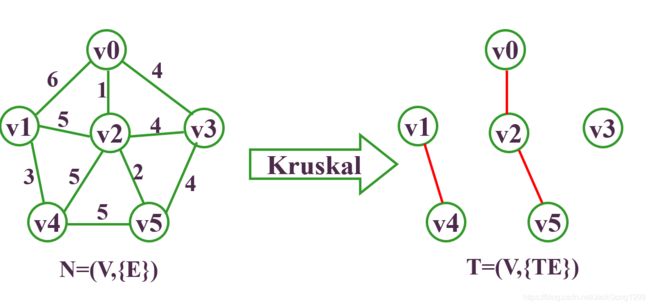
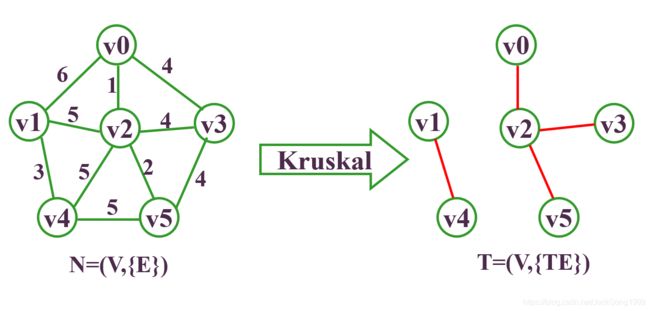
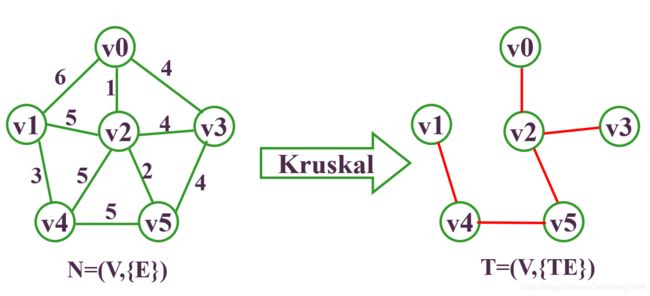
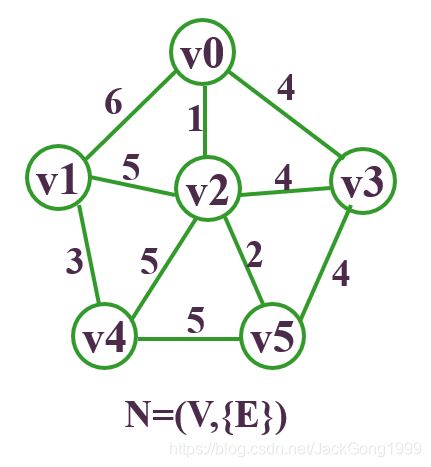
假如现在有如下的连通图:
要求它的最小生成树,则步骤为:
Kurskal算法的时间复杂度为:O(e*loge)。只和边数有关,与网中的顶点数无关,适合求边稀疏的网的最小生成树。
代码具体实现如下:
- 输入边,用结构体储存
- 用结构体快排以边比较从小到大快排
- 建一个并查集,并初始化并查集(并查集代表两个点有没有在同一个树里面
设边edges[100000],edges.start一个点,edges.to另一个点,edge.weight是边长,total是最终答案。
- for(i=1;i<=m(边数);i++)找一条边edges[i],若edges[i].start与edges[i].to不在同一个并查集里面,就将edges[i].start与edges[i].to所在的并查集合并,并将total+=edge[i].weight。
- 若在同一个并查集,则跳过这次循环。因为如果这两个点连接起来,就会形成一个环。
注意:当到了已连边的个数是点的个数-1时,就要停止循环,因为这个时候,最小生成树已经完成了,所有的并查集都连在了一起。
#include
using namespace std;
struct edge{
int start;
int to;
long long weight;
}edges[200100];
int f[200005];
int m,n,i,j,u,v,total;
long long result;
//并查集
int finds(int x){
if(x==f[x]){
return x;
}else{
f[x]=finds(f[x]);
return f[x];
}
}
void createMinSpanTreeKruskal(){
for(i=1;i<=m;i++){
u=finds(edges[i].start);
v=finds(edges[i].to);
if(u==v){
continue;
}
f[u]=v;
result+=edges[i].weight;
total++;
if(total==n-1){
break;
}
}
}
bool cmp(edge e1,edge e2){
return e1.weight
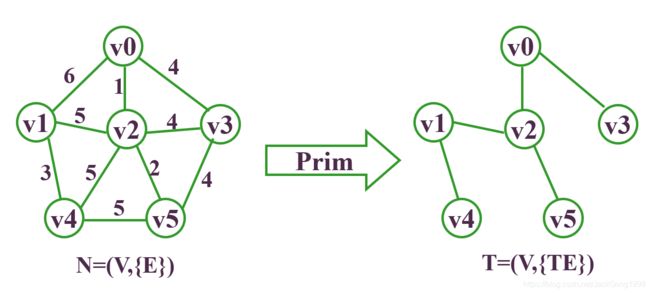
接下来介绍Prim算法
Prim算法的基本思想:首先以一个结点作为最小生成树的初始结点,然后以迭代的方式找出与最小生成树中各结点权重最小边,并加入到最小生成树中。加入之后如果产生回路则跳过这条边,选择下一个结点。当所有结点都加入到最小生成树中之后,就找出了连通图中的最小生成树了。(有点像求最短路径里面的迪杰斯特拉算法)
Prim算法的基本步骤:
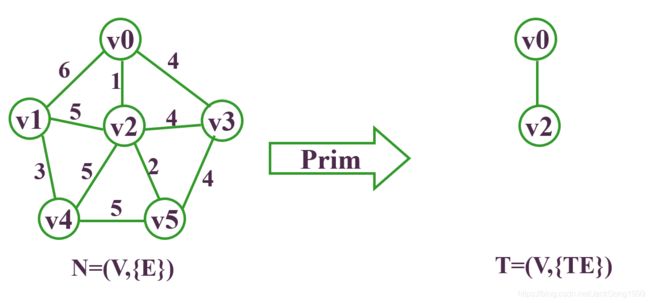
设N=(V,{E})是连通网,T=(V,{TE})表示N的最小生成树,TE为最小生成树边的集合,初始为空集。则Prim算法的执行过程:
Step1:令U={u},u∈V(u是网中任意一个顶点),TE={};
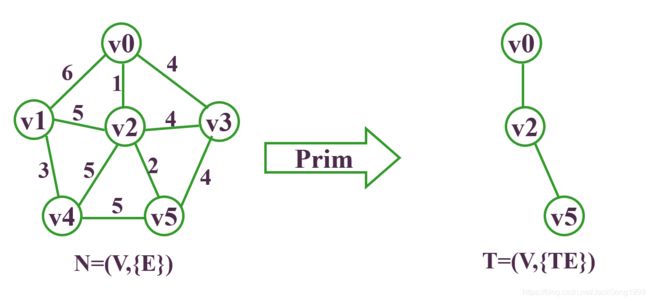
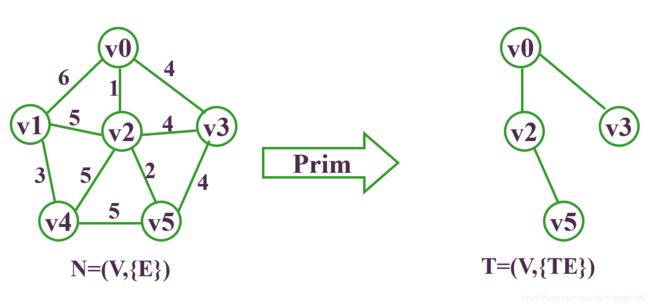
Step2:在u∈U,v∈V-U的边(u,v)∈E中寻找一条代价最小的边(u,v)并入TE,同时将顶点v并入U;
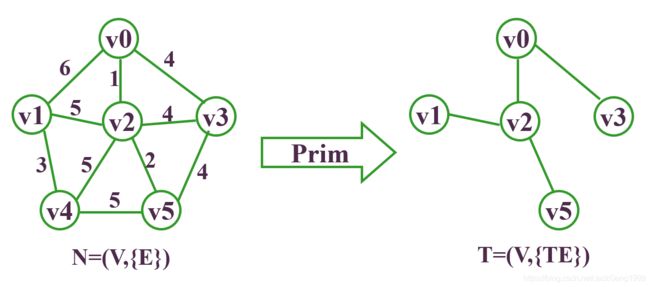
Step3:重复Step2,直至U=V,此时TE中必有n-1条边,而T={V,{TE}}是N的一棵最小生成树。
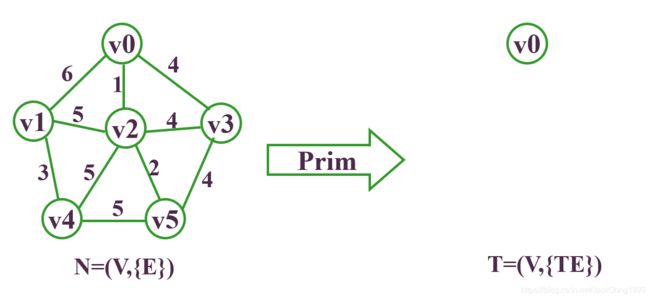
先还假设上面Kruskal的连通图:
要求它的最小生成树,则步骤为:
至此,得到最小生成树。
Prim算法的时间复杂度为:O(n*n),只和顶点数有关,与网中的边数无关。适用于求边稠密的最小生成树。
实现代码如下:
#include
using namespace std;
const int INF=INT_MAX;
int n,m;
int w[5005][5005];//用于记录所有边的关系
int lowcost[5005];//用于记录距离树的距离最短路程
void createMinSpanTreePrim(){
int i,j,sum=0,minn,minIndex;
//初始化最小花费数组,默认先把离1点最近的找出来放好
for(i=1;i<=n;i++){
lowcost[i]=w[1][i];
}
lowcost[1]=0; //记录1已经被访问过了,所以lowcost变为0
for(i=1;i Prim算法和Kruskal算法对比:
从策略上来说,Prim算法是直接查找,多次寻找邻边的权重最小值,而Kruskal是需要先对权重排序后查找的。
所以说,Kruskal在算法效率上是比Prim快的,因为Kruskal只需一次对权重的排序就能找到最小生成树,而Prim算法需要多次对邻边排序才能找到。
这点也能从洛谷评判时间上看出来。(当然,在这里写的Prim算法属于最基本的无优化的算法,耗时巨长,也贼费空间。大佬们的各种牛皮算法如优先队列+堆优化等,本蒟蒻还得多加学习)