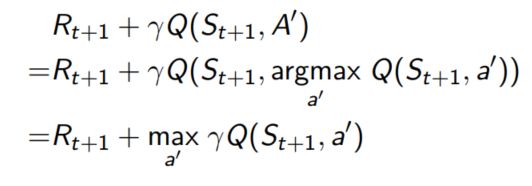强化学习笔记(4)无模型控制Model-Free Control(On-policy learning, off-policy learning, GLIE, Sarsa, Q-learning)
文章目录
- Introduction
- 概念
- On-Policy learning
- Off-Policy learning
- Monte-Carlo Control
- 问题1:使用行为价值函数代替状态价值函数
- 贪婪策略基于行为价值函数的更新:
- 问题2:使用贪婪算法的局限性
- 例
- 解决方案: ϵ − g r e e d y \epsilon-greedy ϵ−greedy
- GLIE
- 定理:
- GLIE Monte-Carlo Control
- 定理
- TD Control
- Sarsa
- 算法描述
- 定理
- 缺点:
- S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)
- n-step Sarsa
- n-step Q-return (n步Q收获)定义
- n-step Sarsa 通过n-step Q-return 更新公式
- q λ q^\lambda qλ
- S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ) Forward view
- Backward View S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)
- S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)算法描述
- Off-Policy learning(借鉴学习策略)
- Q-learning
- 估计不同分布的数学期望
- TD Q-learning
- 状态价值函数公式
- 转换状态行为对价值函数Q(s,a)
- 算法描述
Introduction
前面所说的MC、TD、TD( λ \lambda λ)都是不依赖模型的情况下如何 预测。即求解给定策略下的状态价值或者行为价值函数。
现在所有解决的问题是: 不基于模型条件下,如何优化个体学习的价值函数,同时提升自身策略,是不基于模型的控制问题
一些可以解决的问题:
- 电梯调度
- 直升机特技飞行
- 机器人行走
- 打电子游戏
特点:
- MDP模型未知,但是可以利用经验。
- MDP模型已知,但是问题规模过大。
概念
On-Policy learning
-
Learn On the job。利用当前的去学习
-
利用策略 π \pi π所得到的经验 去优化策略 π \pi π
Off-Policy learning
- “站在巨人的肩膀上学习”
- 利用其它的策略所获得的经验去学习优化策略 π \pi π
Monte-Carlo Control
问题1:使用行为价值函数代替状态价值函数
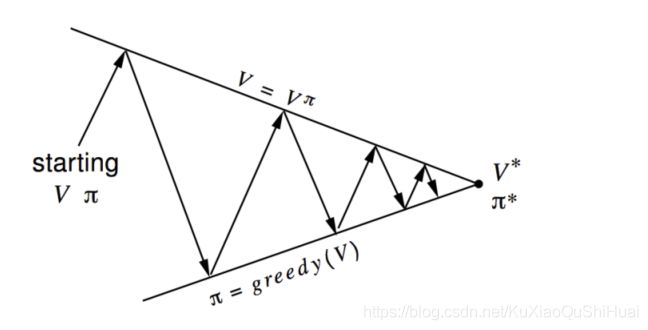
控制过程就是策略优化的过程。可以按照动态规划的思路。在价值函数策略更新之间不断的迭代。最终达到最优。
如果想要达到这个效果,就需要求出在策略 π \pi π下状态价值函数V。
贪婪策略基于状态价值的更新,需要知道整个MDP模型。因为
π ′ ( s ) = a r g m a x a ∈ A ( R s a + P s s ′ a V ( s ′ ) ) \pi'(s) = argmax_{a \in A} (R_s^a + P_{ss'}^a V(s')) π′(s)=argmaxa∈A(Rsa+Pss′aV(s′))
贪婪策略基于行为价值函数的更新:
π ′ ( s ) = a r g m a x a ∈ A Q ( s , a ) \pi'(s) = arg max_{a\in A}Q(s,a) π′(s)=argmaxa∈AQ(s,a)
可见基于行为价值函数的策略更新,是不需要知道模型信息的,无需各个 状态之间的转换概率 P s s ′ a P_{ss'}^a Pss′a。是model-free。MC算法本身就是就是model-free的。所以使用Q状态价值函数更加方便。
问题2:使用贪婪算法的局限性
动态规划中,第一次使用uniform random policy(均一随机策略),一次迭代之后,开始使用贪婪策略加快速度。最终能够收敛到最优解。
但是在model free中,由于不知道整体的环境,一般不能收敛到最优解,有可能落到局部最优。如果价值更高的状态使用贪婪算法将无法探索到,价值低的也很难再次被经历。
例
有很多品牌的糖果。小明一开始购买了品牌A的某一个口味,打分5.0。 然后又买了B品牌的某个口味,觉得很好吃,打了9分。如果是贪婪策略,第三次小明应该还是购买B品牌,这次打分6分。经过三次之后,A品牌平均分是5纷,B品牌是7.5平均分。所以贪婪策略告诉小明第四次还是B品牌,这次打分是7分。
B一定比A好吗? 不一定,因为小明只尝试了A品牌的某个口味的,可能其他的都更好。
B一定是最好的吗?不,还有很多品牌没有尝试,所以就不能够作为参考。
解决方案: ϵ − g r e e d y \epsilon-greedy ϵ−greedy
解决这个问题的方法就是使用不完全贪婪策略( ϵ − g r e e d y \epsilon-greedy ϵ−greedy)。
在每次进行选择时,
-
ϵ \epsilon ϵ的概率去随机选择,从而保证探索的广度。
-
(1- ϵ \epsilon ϵ )的概率去使用贪婪策略。
在策略 π \pi π,状态s下,执行动作a的概率:
KaTeX parse error: Undefined control sequence: \cal at position 86: … argmax_{a \in \̲c̲a̲l̲ ̲A} Q(s,a)\\ \ep…
定理证明:
GLIE
Greedy in the Limit with Infinite Exploration
-
所有的状态动作对都被探索无数次
lim k → ∞ N k ( s , a ) = ∞ \lim_{k \rightarrow \infin} N_k(s,a) = \infin k→∞limNk(s,a)=∞ -
随着采样趋向于无穷,策略收敛于贪婪策略
KaTeX parse error: Undefined control sequence: \cal at position 66: …rg\max_{a' \in \̲c̲a̲l̲ ̲A}Q_k(s,a'))
定理:
GLIE MC控制能收敛到最优的状态行为价值函数。
GLIE Monte-Carlo Control
- 第k次采样,使用策略 π \pi π :{ S 1 , A 1 , R 2 , . . . S T S_1,A_1,R_2, ... S_T S1,A1,R2,...ST} ~$ \pi$
- 对于每个序列中的状态和动作,例如 S t S_t St和 A t A_t At
N ( S t , A t ) ← N ( S t , A t ) + 1 Q ( S t , A t ) ← Q ( S t , A t ) + 1 N ( S t , A t ) ( G t − Q ( S t , A t ) ) N(S_t,A_t) \leftarrow N(S_t, A_t) +1 \\ Q(S_t , A_t) \leftarrow Q(S_t, A_t) + \frac{1}{N(S_t,A_t)}(G_t - Q(S_t,A_t)) N(St,At)←N(St,At)+1Q(St,At)←Q(St,At)+N(St,At)1(Gt−Q(St,At))
- 基于动作价值函数提升策略
ϵ ← 1 / k π ← ϵ − g r e e d y ( Q ) \epsilon \leftarrow 1/k \\ \pi \leftarrow \epsilon-greedy(Q) ϵ←1/kπ←ϵ−greedy(Q)
定理
GLIE Monte-Carlo control 收敛于最优行为价值函数。 Q ( s , a ) → q ∗ ( s , a ) Q(s,a) \rightarrow q_*(s,a) Q(s,a)→q∗(s,a)
TD Control
Sarsa
利用MC控制的思路:
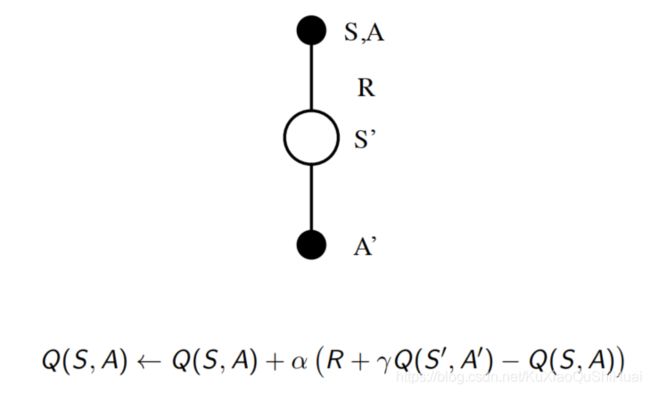
SARSA名称的来历如图。
不同于MC在整个序列结束后更新。Sarsa是在每个时间步,如图,状态S之后的S‘确定采取行为A’后,对状态行为价值对Q(S,A)进行更新。
使用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy策略
算法描述
输入:episodes(序列), α \alpha α(学习率), γ \gamma γ(衰减因子)
输出:Q
初始化:对于每个状态集合KaTeX parse error: Undefined control sequence: \cal at position 1: \̲c̲a̲l̲{s}里的状态s和动作集合KaTeX parse error: Undefined control sequence: \cal at position 1: \̲c̲a̲l̲ ̲A(s)里的动作a,任意设置Q(s,a)的值; 设置Q(终止状态,·)= 0
对于每个序列:
初始化:S=序列的第一个状态
A= policy(Q,S) // 可以使不完全贪婪策略
对于序列的每一步:
R,S'= perform_action(S,A)
A' = policy(Q,S')
Q(S,A) = Q(S,A) + \alpha(R+ \gamma * Q(S',A') - Q(S,A))
S = S'; A = A';
直到终止状态
直到所有序列都被访问
定理
当一下条件成立,Sarsa收敛到最优的行为价值函数 Q ( s , a ) → q ∗ ( s , a ) Q(s,a) \rightarrow q_*(s,a) Q(s,a)→q∗(s,a):
-
GLIE 特性
-
Robbins-Monro sequence of step-sizes α t \alpha_t αt (学习率满足)
∑ t = 1 ∞ α t = ∞ ∑ t = 1 ∞ α t 2 < ∞ \sum_{t=1}^{\infin} \alpha_t = \infin \\ \sum_{t=1}^{\infin} \alpha_t^2 < \infin t=1∑∞αt=∞t=1∑∞αt2<∞
缺点:
- Q(S,A)是用一张大表来存储,这不适合大规模问题。
S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)
n-step Sarsa
是根据n-step TD来的。
n-step Q-return (n步Q收获)定义
q t ( n ) = R t + 1 + γ R t + 2 + . . . + γ n − 1 R t + n + γ n Q ( S t + n ) q_t^{(n)} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{n-1}R_{t+n} + \gamma ^{n}Q(S_{t+n}) qt(n)=Rt+1+γRt+2+...+γn−1Rt+n+γnQ(St+n)
n-step Sarsa 通过n-step Q-return 更新公式
Q ( S t , A t ) ← Q ( S t , A t ) + α ( q t ( n ) − Q ( S t , A t ) ) Q(S_t,A_t) \leftarrow Q(S_t, A_t ) + \alpha(q_t^{(n)} - Q(S_t,A_t)) Q(St,At)←Q(St,At)+α(qt(n)−Q(St,At))
q λ q^\lambda qλ
和 T D ( λ ) TD(\lambda) TD(λ)类似,给n-step Q return 的每一步分配一个权重
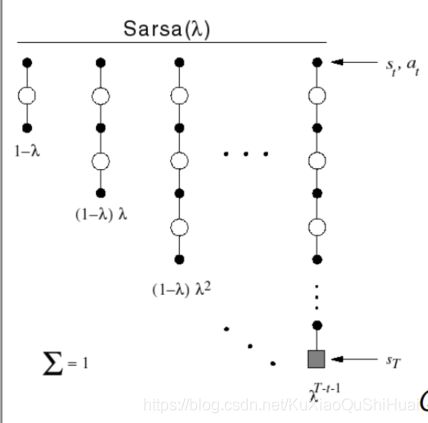
q t λ = ( 1 − λ ) ∑ n = 1 ∞ λ n − 1 q t ( n ) q_t^{\lambda} = (1-\lambda) \sum_{n = 1}^{\infin} \lambda^{n-1} q_t^{(n)} qtλ=(1−λ)n=1∑∞λn−1qt(n)
S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ) Forward view
使用 q t λ q_t^ \lambda qtλ 收获来更新状态行为对的Q值,就可以得到 S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)前向认识
Q ( S t , A t ) ← Q ( S t , A t ) + α ( q t ( λ ) − Q ( S t , A t ) ) Q(S_t,A_t) \leftarrow Q(S_t, A_t) + \alpha(q_t^{(\lambda)} - Q(S_t , A_t)) Q(St,At)←Q(St,At)+α(qt(λ)−Q(St,At))
前向认识需要遍历整个序列,再更新Q价值。
Backward View S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)
-
和 T D ( λ ) TD(\lambda) TD(λ)类似,在online算法中使用效用迹(eligibility traces)
-
但,对于每个状态行为价值对, S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)都有一个eligibility trace
E 0 ( s , a ) = 0 ; E t ( s , a ) = γ λ E t − 1 ( s , a ) + 1 ( S t = s , A t = a ) E_0(s,a) = 0 ;\\ E_t(s,a) = \gamma \lambda E_{t-1}(s,a) + 1(S_t = s, A_t = a) E0(s,a)=0;Et(s,a)=γλEt−1(s,a)+1(St=s,At=a)
体现的是一个结果与某个状态行为对的因果关系 -
更新公式:( δ t \delta_t δt是TD-error, E t ( s , a ) E_t(s,a) Et(s,a)是Eligibility trace)
δ t = R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) Q ( s , a ) ← Q ( s , a ) + α δ t E t ( s , a ) \delta_t = R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) \\ Q(s,a) \leftarrow Q(s,a) + \alpha \delta_t E_t (s,a) δt=Rt+1+γQ(St+1,At+1)−Q(St,At)Q(s,a)←Q(s,a)+αδtEt(s,a)
S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)算法描述
Off-Policy learning(借鉴学习策略)
通过策略 μ ( a ∣ s ) \mu(a|s) μ(a∣s) 生成行为, 但是更新 状态行为对的价值时采用目标策略 π ( a ∣ s ) \pi(a|s) π(a∣s)。 目标策略 π \pi π是一个相对更好的策略。例如借鉴人的已有经验或者其他的agent所学内容。
包括基于MC的和基于TD的。基于MC目前仅有理论上的研究价值。实际应用不大。
Q-learning
估计不同分布的数学期望
E X ∼ P [ f ( x ) ] = ∑ P ( x ) f ( x ) = ∑ Q ( x ) P ( x ) Q ( x ) f ( x ) = E X ∼ Q [ P ( x ) Q ( x ) f ( x ) ] \mathbb E_{X \sim P}[f(x)] = \sum P(x)f(x) \\ =\sum Q(x) \frac{P(x)}{Q(x)}f(x) \\ = \mathbb E_{X\sim Q} [\frac{P(x)}{Q(x)}f(x)] EX∼P[f(x)]=∑P(x)f(x)=∑Q(x)Q(x)P(x)f(x)=EX∼Q[Q(x)P(x)f(x)]
TD Q-learning
状态价值函数公式
V ( S t ) ← V ( S t ) + α ( π ( A t ∣ S t ) μ ( A t ∣ S t ) ( R t + 1 + γ V ( S t + 1 ) ) − V ( S t ) ) V(S_t) \leftarrow V(S_t) + \alpha (\frac{\pi(A_t|S_t)}{\mu(A_t|S_t)} (R_{t+1} + \gamma V(S_{t+1})) - V(S_t)) V(St)←V(St)+α(μ(At∣St)π(At∣St)(Rt+1+γV(St+1))−V(St))
理解:
在状态S_t 中,按照策略 μ \mu μ产生了一个行为 A t A_t At , 执行这个行为后进入状态 S t + 1 S_{t+1} St+1。
μ ( A t ∣ S t ) \mu(A_t|S_t) μ(At∣St)代表行为策略在状态 S t S_t St下产生动作 A t A_t At的概率
π ( A t ∣ S t ) \pi(A_t | S_t) π(At∣St)代表借鉴的策略在状态 S t S_t St下产生动作 A t A_t At的概率
-
如果两个策略下的概率比值接近1,说明这两种策略在状态 S t S_t St时采取 A t A_t At的概率是相同的。
-
如果比值很小,说明借鉴策略和当前策略所做选择很大程度都不一样。没有借鉴的意义,系数很小。
-
如果比值很大,说明借鉴策略选择行为 A t A_t At的可能性要大于当前策略,所以很有借鉴意义,系数很大。
转换状态行为对价值函数Q(s,a)
-
当前动作下一个状态是根据策略 μ \mu μ来的。即 A t + 1 ∼ μ ( ⋅ ∣ s ) A_{t+1} \sim \mu(· | s) At+1∼μ(⋅∣s)
-
认为接下来的可替换的动作 A ′ ∼ π ( ⋅ ∣ S t ) A' \sim \pi(· | S_t) A′∼π(⋅∣St)
-
通过可替换动作A’来更新 Q ( S t , A t ) Q(S_t, A_t) Q(St,At)
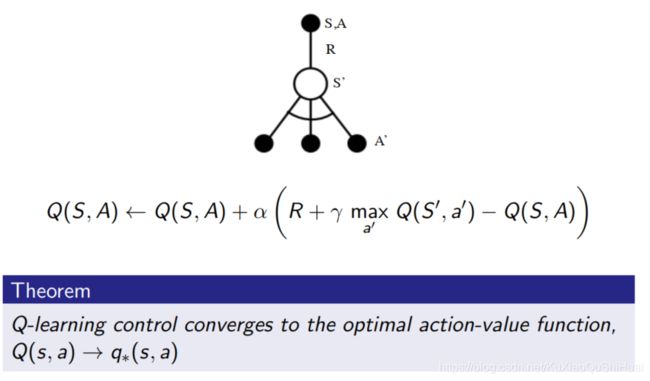
Q ( S t , A t ) ← Q ( S t , A t ) + α ( R t + 1 + γ Q ( S t + 1 , A ′ ) − Q ( S t , A t ) ) Q(S_t, A_t) \leftarrow Q(S_t,A_t) + \alpha (R_{t+1} + \gamma Q(S_{t+1}, A') - Q(S_t,A_t)) Q(St,At)←Q(St,At)+α(Rt+1+γQ(St+1,A′)−Q(St,At))
行为策略 μ \mu μ是基于行为价值函数 Q ( s , a ) , ϵ − Q(s,a), \epsilon- Q(s,a),ϵ−贪婪策略
借鉴策略 π \pi π则是基于 Q ( s , a ) Q(s,a) Q(s,a)的完全贪婪策略。
$R_{t+1} + \gamma Q(S_{t+1}, A’) KaTeX parse error: Undefined control sequence: \是 at position 1: \̲是̲基于**借鉴策略\pi ∗ ∗ 产 生 的 行 为 A ′ 得 到 的 Q 值 。 根 据 这 种 更 新 方 式 , 状 态 S t 依 据 ∗ ∗ 不 完 全 贪 婪 策 略 ∗ ∗ 得 到 的 行 为 A t 的 价 值 将 朝 着 下 一 个 状 态 **产生的行为A' 得到的Q值。根据这种更新方式,状态S_t依据**不完全贪婪策略**得到的行为A_t的价值将朝着下一个状态 ∗∗产生的行为A′得到的Q值。根据这种更新方式,状态St依据∗∗不完全贪婪策略∗∗得到的行为At的价值将朝着下一个状态S_{t+1}$下贪婪策略确定的方向按照一定比例更新。
这样既能够保证 μ \mu μ策略更加接近贪婪策略,同时保证个体持续探索并经历足够丰富的新状态。
最终: