Deep Recurrent Q-learing for POMDP论文笔记
DQN主要有两个缺点:记忆限制,以及每一次决策都需要完整的游戏画面。这篇文章将DQN的第一个全连接层换成了LSTM,以求解决这些问题。这是因为LSTM具有记忆单元,可以记住以往历史信息。
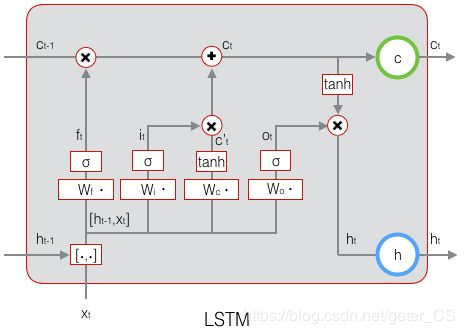
虽然这DRQN每个时间步只能看到一帧,但是它可以整合时间信息,并且复现DQN的效果。此外,在接受部分观察进行训练并通过逐步更完整的观察进行评估时,DRQN的表现与观测信息成一定的函数关系。反过来,若是使用完整观察训练,并石永红部分观察信息评估时,DRQN的表现要比DQN差。
给定相同的历史长度,重复性是在DQN的输入层中堆叠历史帧的可行替代方法。虽然DRQN并没有带来整体性优势,但是在评估时,它可以更好的适应观察质量的变化。
DQN使用输入是Agent所遇到的最近的4个状态(帧)构成的。因此对于对于需要记住更多帧的游戏,它就不适用了。换句话说,任何需要超过四帧记忆的游戏都会显示非马尔可夫性,因为未来的游戏状态(和奖励)不仅仅取决于当前输入。这类游戏就变成了POMDP(Partially-Observable Markov Decision Process,部分可观测的马尔科夫决策过程)问题。而大多数强化学习方法是基于马尔科夫性质的,包括Q-learning,因此对于POMDP问题DQN就不适用了。
真实世界中的任务由于特征化的是不完整的带噪声的状态,因此会导致部分可观测性质。因此实际上许多Atari 2600游戏都是POMDP问题,比如在Pong中,你只能通过屏幕知道位置信息,但是不能获取速度信息。
Q学习和深度Q学习
POMDP
强化学习通常描述为4元组 ( S , A , P , R ) (S,A,P,R) (S,A,P,R),其中 s t ∼ S s_t\sim S st∼S是状态集合, a t ∼ A a_t \sim A at∼A是动作集合, s t + 1 ∼ P ( s t , a t ) s_{t+1}\sim P(s_t,a_t) st+1∼P(st,at)是转移概率, r t ∼ R ( s t , a t ) r_{t}\sim R(s_t,a_t) rt∼R(st,at)是奖赏函数。而一个POMDP问题可以描述为一个6元组 ( S , A , P , R , Ω , O ) (S,A,P,R,\Omega ,O) (S,A,P,R,Ω,O)。Agent接收的不在是state状态而是观察 o ∈ Ω o\in \Omega o∈Ω。观察是生成于概率分布 o ∼ O ( s ) o\sim O(s) o∼O(s)。深度Q-Learning没有明确的机制破译POMDP的基本状态,只有在观察反映基础系统状态时才有效(也就是o等效于s时)。一般来说通过观察评估的Q值不等于状态Q值,也就是 Q ( o , a ∣ θ ) ≠ Q ( s , a ∣ θ ) Q(o,a|\theta)\neq Q(s,a|\theta) Q(o,a∣θ)̸=Q(s,a∣θ)。而DRQN中加入LSTM网络可以更好估计基础(潜在,表面之下的)系统状态,并且可以减小 Q ( o , a ∣ θ ) Q(o,a|\theta) Q(o,a∣θ) 和 Q ( s , a ∣ θ ) Q(s,a|\theta) Q(s,a∣θ)之间的差距。换句话说,DRQN可以从序列观测更好的估计实际Q值,也就是可以在部分可观测环境中学到一个更好的策略。
DRQN结构
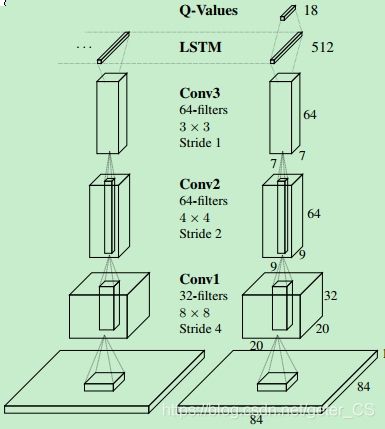
从图中可以看出DRQN就是将第一个全连接层用LSTM进行了替换。注意,每个时刻的输入,先进入卷积,然后在作为每个时刻LSTM的输入。这张图中显示的是最近的两个时间步。
更新
自举序列更新:从经验池随机抽取情节(复数),并且从情节开始进行更新直到情节结束。目标值由目标网络生成。RNN的隐藏状态始终贯穿整个情节。
自举随机更新:从经验池随机抽取情节(复数),并且随机从情节某步开始,只进行一定的迭代时间步长(例如只向后一步也就是o是 ( s t − 1 , s t ) (s_{t-1},s_{t}) (st−1,st))。目标值由目标网络生成。RNN的初始状态更新开始设置为0。
自举序列更新好处是LSTM的隐藏状态可以贯穿整个情节。然而这样与DQN随机抽样策略相冲突(也就是深度学习样本独立同分布的条件)。自举随机更新虽然满足随机抽样,但是LSTM的隐藏状态在每次更新开始时都是0(而序列更新只在每个情节第一步更新时是0)。将隐藏状态归零使得LSTM更难以学习跨越时间尺度的函数,而不是通过时间反向传播达到的时间步长数。实验显示这两个都是可行的,并且在一系列game上性能相似。在这篇paper中使用的自举随机更新,因为更加简单一点。而且作者也认为这些结果也可以扩展到自举序列更新上。
由于DQN将Atari游戏的全状态看做是最近4帧,因此大多数游戏变为了MDPs。
为了在不减少输入帧数条件下介绍部分可观测性,文章探索对Pong做特殊改动。
闪烁Pong
也就是每个时间步,对于Pong,有0.5的概率屏幕是完全模糊的。这使得Pong变为了一个POMDP问题。
为了解决这个问题,整合帧之间的信息来估计球的位置、速度等的变化是必要的。由于一半的帧在期望中被模糊,因此成功的玩家必须对几个可能连续的模糊输入具有鲁棒性。文中训练3种类型的网络来播放闪烁乒乓:1帧DRQN,标准的4帧DQN和增强的10帧DQN。 如图4a所示,为DQN提供更多帧可以提高性能。 然而,即使有10帧的历史,DQN仍然难以获得积极的分数。
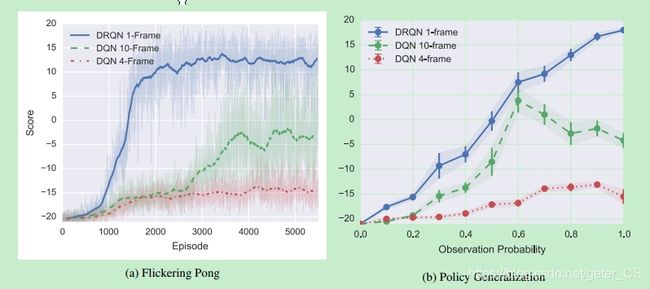 尽管只有一帧输入,DRQN在处理嘈杂感觉方面比DQN更有能力。 图b说的是在0.5模糊概率下训练好的这三种策略在其他概率下的泛化能力。
尽管只有一帧输入,DRQN在处理嘈杂感觉方面比DQN更有能力。 图b说的是在0.5模糊概率下训练好的这三种策略在其他概率下的泛化能力。

10帧DQN学到的卷积过滤器样本,每一行绘制触发特定层中特定的卷积过滤器的最大激活的输入帧(难译)。红色边界框说明了
导致最大激活的输入图像部分。第一卷积层中的大多数滤波器仅检测到球拍。而第二层开始检测球运动的具体方向。几乎所有的Conv3过滤器都可以跟踪球和球拍的相互作用,包括偏转,球速和运行方向
。尽管一次看到一帧,但各个LSTM单元也分别检测到高级事件:
丢球,球反射,球反射离墙。 每个图像叠加代理看到的最后10帧,为更近的帧提供更多亮度。