Leetcode之单调栈题目解答----基于python3

一、单调栈

顾名思义，单调栈就是栈里面存放的数据都是有序的，所以可以分为单调递增栈和单调递减栈两种。
单调递增栈就是从栈底到栈顶是从大到小。
单调递减栈就是从栈底到栈顶是从小到大。
基于它的特性，其十分适合处理列表中相邻元素比较大小相关的题目，这里以python3为例，给出LeetCode中的几个例子。代码均是博主自己写的，如有可提升效率之处请留言讨论。
题目主要有:
第42题—接雨水
第84题—柱状图中最大的矩形
第496题—下一个更大的元素I
第739题—每日温度

二、LeetCode例子

2.1 第42题—接雨水

2.1.1 题目描述

42.接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

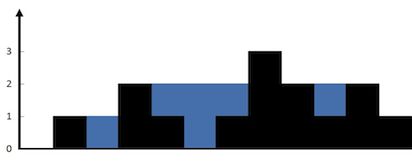
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

2.1.2 思路和解答

首先，显然，至少List的长度为3，否则雨水为0。
其次，显然，需要初始栈，若List中列表头部的元素递增，则存不住雨水，舍去，直到可以初始。
最后，定义从栈底到栈顶单调减的单调栈，相当于每次迭代对三个元素进行计算雨水，分别是高1，低，高2，则可以囤积的雨水为(min(高2，高1)-低)*宽。

class Solution:
    def trap(self, height):
        # 使用从栈底到栈顶单调减的单调栈
        if len(height) < 3 : return 0
        for i in range(len(height)-1):
            if height[i] <= height[i+1]:
                continue
            else:
                stack = [i, i + 1]
                break
        if i == len(height)-1: return 0

        rain_v = 0
        for index in range(i+2, len(height)):
            h = height[index]
            while len(stack) > 1 and h > height[stack[-1]]:
                current_index = stack[-1]
                stack.pop(-1)
                H = min(h, height[stack[-1]]) - height[current_index]
                W = index - stack[-1] - 1
                rain_v += H * W
            if height[stack[-1]] < h: stack.pop(-1)
            stack.append(index)
        return rain_v

2.2 第84题—柱状图中最大的矩形

2.2.1 题目描述

84. 柱状图中最大的矩形
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

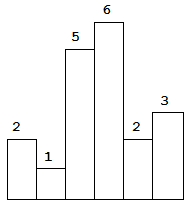
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3].

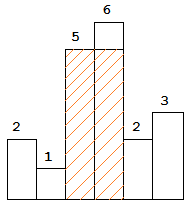
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

输入: [2,1,5,6,2,3]
输出: 10

2.2.2 思路和解答

使用单调栈，从栈低到栈顶单调增，如果不符合，则弹出，并计算面积。
单调栈中保存的是当前元素的索引index。
单调栈中先入栈-1,以保存当前索引的"左边界"，即不大于当前值的最大索引
面积的宽度为 当前index -左边界 + 1.

class Solution:
    def largestRectangleArea(self, heights):
        stack = [-1] #单调栈，从栈底到栈顶单调增
        heights.append(-1) #List末尾增加-1,保证所有元素都可以出栈
        maxarea = 0
        for index,h in enumerate(heights):
            i = 0
            while len(stack) > 0 and h < heights[stack[-1]]:
                height = heights[stack[-1]]
                width = index - stack[-2] - 1
                stack.pop(-1) #弹出栈顶
                current_area = width * height
                if maxarea < current_area:
                    maxarea = current_area
            stack.append(index)
        return maxarea

2.3 第496题—下一个更大的元素I

2.3.1 题目描述

496. 下一个更大元素 I
给定两个 没有重复元素 的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。找到 nums1 中每个元素在 nums2 中的下一个比其大的值。

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出 -1 。

输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于num1中的数字4，你无法在第二个数组中找到下一个更大的数字，因此输出 -1。
对于num1中的数字1，第二个数组中数字1右边的下一个较大数字是 3。
对于num1中的数字2，第二个数组中没有下一个更大的数字，因此输出 -1。

2.3.2 思路和解答

典型的单调栈可解决问题，构造单调增的单调栈即可。

class Solution:
    def nextGreaterElement(self, nums1, nums2):
        # 构造单调增的单调栈
        results = [-1] * len(nums1)
        stack = []
        for index, num2 in enumerate(nums2):
            while stack != [] and num2 > stack[-1]:
                peak = stack[-1]
                stack.pop(-1)
                if peak in nums1:
                    results[nums1.index(peak)] = num2
            stack.append(num2)

        return results

2.4 第739题—每日温度

2.4.1 题目描述

739. 每日温度
请根据每日 气温 列表，重新生成一个列表。对应位置的输出为：要想观测到更高的气温，至少需要等待的天数。如果气温在这之后都不会升高，请在该位置用 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

2.4.2 思路和解答

定义从栈底到栈顶单调减的单调栈.
栈内保存温度数据的索引index.
若不满足，则出栈，出栈时，意味着其需要等待当前index-出栈index天.

class Solution:
    def dailyTemperatures(self, T: List[int]) -> List[int]: 
        # 使用从栈底到栈顶单调减的单调栈
        stack = []
        result = [0] * len(T)
        for index, t in enumerate(T):
            while stack!=[] and T[stack[-1]] < t:
                i = stack[-1]
                stack.pop(-1)
                result[i] = index - i
            stack.append(index)
        return result