【深度之眼吴恩达机器学习第四期】笔记（八）

SVM

从逻辑回归到SVM

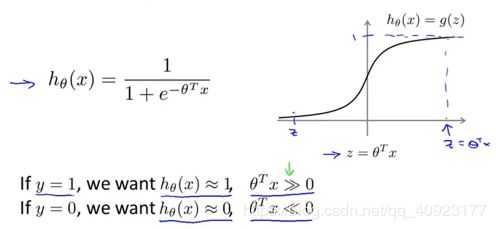
在逻辑回归中，如果标签y=1，我们希望预测值也等于1，那么就需要θ^Tx远远大于0；相反，如果标签y=0，那么就需要θ^Tx远远小于0。

这时候使用的损失函数如下：

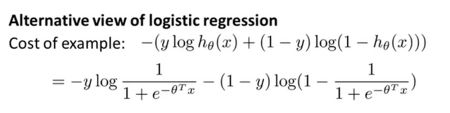
根据上面的损失函数，所有样本点在逻辑回归中都会一直产生损失，就会一直对所有点都进行优化。
但是样本点在越过决策边界一定距离后其实是比较安全的，也就是说置信度比较高。那么我们可不可以不考虑这些点，只关注置信度比较低的点和误分类的点？
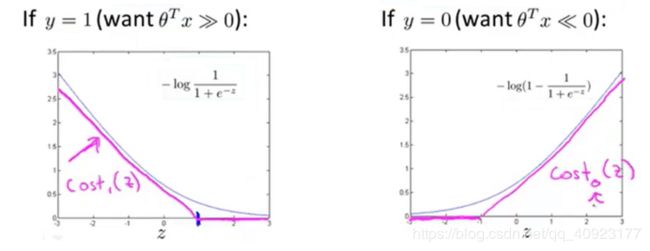
这就是hinge损失的想法，θ^Tx在大于1（y=1）或小于-1时（y=0）不会产生损失。至于为什么是1和-1后面有解释。
hinge损失如下图的粉红色线所示，两个hinge函数分别记为cost₁(z)和cost₀(z)。

这时候的损失函数为：

由于乘以常数并不会影响最小化的参数结果：

又由于1/m和λ是常数，所以可以对损失函数乘以m/λ，再令1/λ=C，得到的损失函数如下所示：

由于1/λ=C，所以如果C很大，就代表λ很小，这时候就容易过拟合，SVM分类器就容易受到噪声的干扰，更可能选择粉红色的决策边界而不是黑色的决策边界。

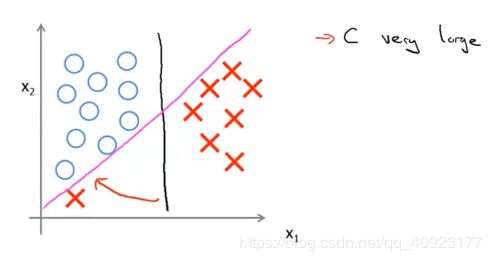
如果对于上面的损失函数，我们加上一些约束条件（强制要求所有的点都分类正确且置信度较高）：

那么损失函数的前一项就是0（看看hing损失的图），这时候的损失函数为：

这和网上的表达式本质上是相同的:

1. 1/2是常数，所以可以消去;
2. θ²求和其实就是‖W‖²，又因为‖W‖是正有理数，所以min{‖W‖²}→min{‖W‖}=max{1/‖W‖};
3. θ^Tx就是W^Tx+b，再把yⁱ=0改为yⁱ=-1就可以得到下面式子中的约束条件。
   

间隔最大理解SVM

SVM全名叫支持向量机，对于SVM来说，它并不满足于用决策边界把数据分类正确，它还想要得到的分类器的鲁棒性最好。下图中的黑色、绿色和粉色的决策边界都可以得到正确的分类器，但是只有黑色的决策边界鲁棒性最好。
在决策边界取黑色线的情况下，两个蓝色的点和一个红色的点离决策边界最近，这些点就是支持向量，点所在的平面称为支撑平面，点到决策边界的距离称为间隔，鲁棒性好也就是间隔最大。

上面提到θ^Tx(也就是W^Tx+b)在大于1（y=1）或小于-1时（y=0）不会产生损失，这个1其实就是间隔z。所以决策边界的数学表达式是W^Tx+b=0，两个蓝色的点所在的直线是W^Tx+b=z，红色点所在的直线是W^Tx+b=-z。
间隔最大用数学语言来描述就是：

表达式忽略y_i就是点到直线的距离，加上y_i是为了使表达式>0。
这个表达式用文字的语言来表达就是：找到离决策边界最近的点（支持向量），使这些点到决策边界的距离（间隔）最大。

如果一组(W,b,x_i)使得L₁=C，y_i(W^Tx_i+b)=z，那么(2W,2b,x_i)也能使L₁=C，也就是说有无数组(W,b,x_i)使得L₁=C。

但两组数据事实上都代表同一个决策边界（2W^Tx_i+2b=0和W^Tx_i+b=0是同一个决策边界）。

那么W/z和b/z也能使L₁=C，这时候y_i(W^Tx_i+b)=1，使得表达式为：

总的来说，同一个决策边界有无数组(W,b)，我们选择了能使y_i(W^Tx_i+b)=1的一组。

直觉上来理解SVM

先回顾一下向量的运算，v^Tu=u^Tv=p‖u‖=u₁u₂+v₁v₂，其中p为向量v在向量u上的投影（图中红色线段），p可正可负。

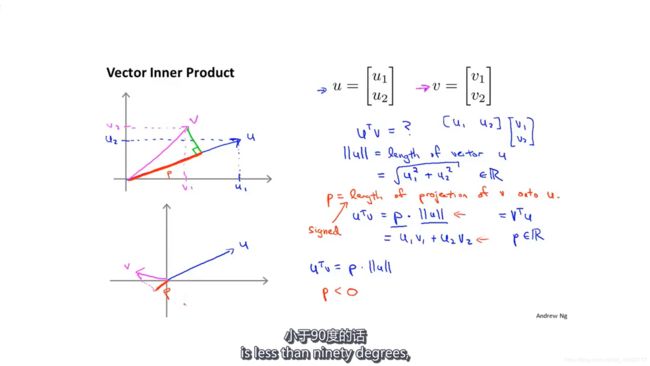
再修改一下之前的表达形式：

1. 为了简单化，令theta0=0，也就是说：决策边界过原点，事实上theta0≠0也是成立的；
2. min{½∑θ²}=min{‖θ‖²/2}；
3. 约束条件里的θ^Tx=p‖θ‖，其中p是x在向量θ上的投影。
   
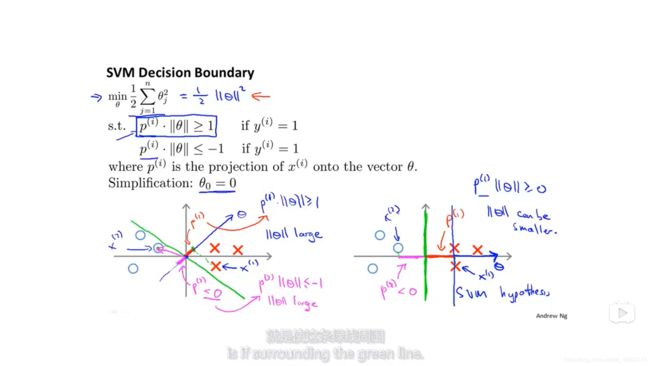
   决策边界上的点代表的向量与theta內积为零，所以theta代表的向量与决策边界正交。（下图的第二个约束条件笔误，应该是y=-1）
   可以看到左边的图中，绿色的线是决策边界，由于离决策边界最近的点（支持向量）在theta向量上的投影（红色和粉红色的线的长度）较短，即p很小。所以由约束条件p‖θ‖≧1（或≦-1）可知‖θ‖需要比较大才能满足约束。
   而在右图中，支持向量在theta上的投影较长，这时候为了满足约束，就可以使用小一点的‖θ‖。
   而函数想要最小化的正好也是‖θ‖，所以，支持向量机会倾向于选择右边的决策边界。
   

核函数

为什么要使用核函数？

的对偶形式如下所示（怎么得出来的请参考《统计学习方法》7.1.4节，或者可以去看JULY的这篇文章）：

上面的表达式中有內积i,x_j>，如果我们的数据集线性不可分，那么可以把数据投影到高维空间，这时候它可能就线性可分了。

假设投影后的x_i，x_j分别为F(x_i)，F(x_j)，那么投影后的內积为i),F(x_j)>。

也就是说我们要先计算出F(x_i)，F(x_j)再计算i),F(x_j)>。

如果我们能找到一个函数使得K(x_i,x_j)=i),F(x_j)>，那么我们就省去了中间的过程，这个K(x_i,x_j)就称为核函数。

但是由于不是投影任一高维都能使线性不可分的数据变得线性可分，现在的问题是投影到哪一个高维？

假设我们手动选择了三个点(l¹,l²,l³)，然后把高斯核函数作为高维向量的元素，也就是说[x₁,x₂]→[f₁,f₂,f₃]

这时候，如果x和 l¹比较接近，那么f¹≈1；
如果x和 l¹相距较远，那么f¹≈0。

把高斯核函数的图像画出来，能更直观的看出它的作用。当x=l¹=[3,5]^T时，f₁的取值最大，随着x与l¹的距离增大，f₁的值也就越小。而σ的大小决定f₁随距离下降的速度。

假设我们学习到的θ=[-0.5,1,1,0]，那么粉红色的点的f=[1,0,0]（离l¹近，离其他两个点远），所以θ^Tf=0.5>0，即该点会被预测为正样本。
蓝色的点离三个选中的点都远，f=[0,0,0]，这时θ^Tf=-0.5<0，会被预测为负样本。
如果对平面上所有的点都进行计算，得到的决策边界大概如红色的线所示，线内的点被预测为正样本，线外的则预测为负样本。

刚才的 l 是手动选的，实际应用中该怎么选呢？
我们会把每个训练点都作为 l，也就是说x是n维的，而f是m+1维的（f₀=1），m是训练数据的个数。在向量f中，有一个f_iⁱ，它是等于1的。

接下来就是用新的高维向量f去训练模型，模型的损失函数和之前的差不多，只有一点要注意，正则项中的n其实是等于m的，因为n是θ的维度，m是训练数据的个数，但是由于现在f是m+1维的，所以θ也是m+1维的，所以n=m。
然后再实际应用中，θ^Tθ会在中间加个M矩阵，变成θ^TMθ，因为在训练集很大的时候，即m很大的时候，θ不好求，所以这样做的原因是为了使θ更好求一些。
C和核函数里的σ都是超参数，需要我们学习的。

在SVM的应用中，要考虑归一化，如果x₁代表房子的面积，x₂代表房间的数量，那么最后学习到的模型就很可能被房子的面积大小所支配，而几乎不考虑房间的数量。

许多SVM的包都有内置的多分类SVM，如果没有的话，我们可以使用K个SVM来训练K分类问题。

如何选择用逻辑回归还是SVM？

1. 当n比m大的时候，可以考虑用逻辑回归或者不使用核函数的SVM，因为训练数据本身就有足够的特征了；
2. 当n比较小而m适中的时候，可以使用带核函数的SVM，这时候它的效果比较好；
3. 当n比较小而m比较大的时候，可以创造一些新的特征值，然后使用逻辑回归或者没有核函数的SVM，因为这时候使用带核函数的SVM会运行得很慢。
4. 当然上面这三种情况都可以使用神经网络，但是神经网络运行的时间比较长，而且SVM不会陷入局部最优，而神经网络有可能会。
   

SVM编程

准备数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat

# 加载数据
raw_data = loadmat('data/ex6data1.mat')
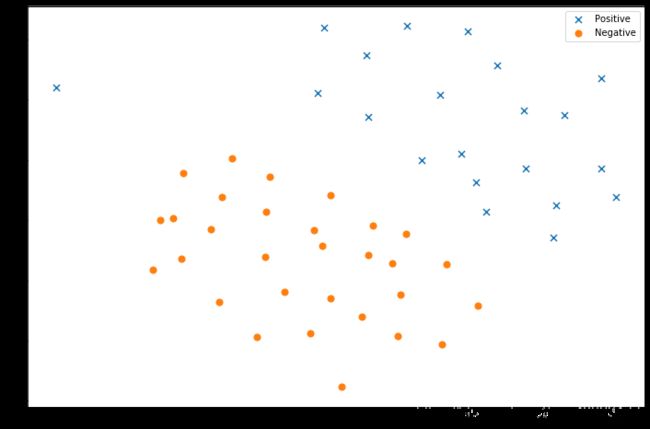
# 把训练数据用散点图画出来
data = pd.DataFrame(raw_data['X'], columns=['X1', 'X2'])
data['y'] = raw_data['y']

# 把数据分为正样本和负样本
positive = data[data['y'].isin([1])]
negative = data[data['y'].isin([0])]

# figsize=(12,8)指定图的大小
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['X1'], positive['X2'], s=50, marker='x', label='Positive')
ax.scatter(negative['X1'], negative['X2'], s=50, marker='o', label='Negative')
# 显示图例，也就是下图中右上角的小方框
ax.legend()
plt.show()

使用SVM训练

from sklearn import svm
svc = svm.LinearSVC(C=1, loss='hinge', max_iter=1000)
svc
# loss='hinge'就是上面损失函数图像中粉红色的线
# LinearSVC(C=1, class_weight=None, dual=True, fit_intercept=True,
#          intercept_scaling=1, loss='hinge', max_iter=1000, multi_class='ovr',
#          penalty='l2', random_state=None, tol=0.0001, verbose=0)
# 训练
svc.fit(data[['X1', 'X2']], data['y'])
# 计算准确率（0.9803921568627451）
svc.score(data[['X1', 'X2']], data['y'])

# 增大参数C，再进行一次训练
svc2 = svm.LinearSVC(C=100, loss='hinge', max_iter=1000)
svc2.fit(data[['X1', 'X2']], data['y'])
# 1.0，C增大代表λ变小，容易过拟合，所以训练集的准确率增大
svc2.score(data[['X1', 'X2']], data['y'])

这时候可能会有一个警告：ConvergenceWarning: Liblinear failed to converge, increase the number of iterations. “the number of iterations.”, ConvergenceWarning)，就是说这次训练在最大的迭代次数内不收敛，希望你增大max_iter这个参数的值。

把刚才的两个训练结果可视化出来

# 函数decision_function()得到的是样本点到决策边界的距离，带正负号
data['SVM 1 Confidence'] = svc.decision_function(data[['X1', 'X2']])
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(data['X1'], data['X2'], s=50, c=data['SVM 1 Confidence'], cmap='seismic')
ax.set_title('SVM (C=1) Decision Confidence')
plt.show()

data['SVM 2 Confidence'] = svc2.decision_function(data[['X1', 'X2']])
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(data['X1'], data['X2'], s=50, c=data['SVM 2 Confidence'], cmap='seismic')
ax.set_title('SVM (C=100) Decision Confidence')
plt.show()

在正距离和负距离的最大值相差不大的时候（如Confidence1中的6和-6）离决策边界越远的点置信度越高，颜色越深；
否则会出现蓝色点表示正距离的情况（如Confidence2中的20和-6）。
但我们这里的数据点的情况是前一种情况。

C=1时，左上角的点本应该是负样本的，也就是红色的，但是这里被预测成立正样本。

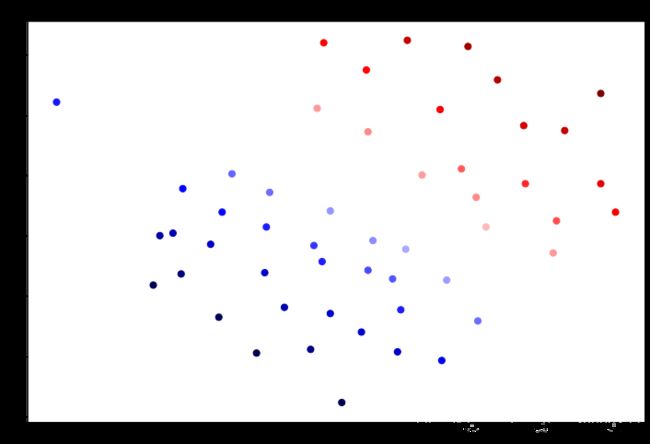
C=100时，过拟合了。虽然左上角的点被预测为负样本，分类正确了，但是它的颜色非常浅，置信度非常低。

定义高斯核函数

def gaussian_kernel(x1, x2, sigma):
# INPUT：两个维度的值x1,x2,高斯核参数sigma
# OUTPUT：高斯核函数计算后的值

    # STEP：计算高斯核函数，这里的输入时向量化的
    return np.exp(-(np.sum((x1-x2)**2))/(2*sigma**2))

x1 = np.array([1.0, 2.0, 1.0])
x2 = np.array([0.0, 4.0, -1.0])
sigma = 2
# 0.32465246735834974
gaussian_kernel(x1, x2, sigma)

导入线性不可分的数据

raw_data = loadmat('data/ex6data2.mat')
data = pd.DataFrame(raw_data['X'], columns=['X1', 'X2'])
data['y'] = raw_data['y']

positive = data[data['y'].isin([1])]
negative = data[data['y'].isin([0])]

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['X1'], positive['X2'], s=30, marker='x', label='Positive')
ax.scatter(negative['X1'], negative['X2'], s=30, marker='o', label='Negative')
ax.legend()
plt.show()

使用带核函数的SVM解决线性不可分的情况

svc = svm.SVC(C=100, gamma=10, probability=True)
svc
# SVC(C=100, cache_size=200, class_weight=None, coef0=0.0,
#    decision_function_shape='ovr', degree=3, gamma=10, kernel='rbf',
#    max_iter=-1, probability=True, random_state=None, shrinking=True, tol=0.001,verbose=False)
# 0.9698725376593279
svc.fit(data[['X1', 'X2']], data['y'])
svc.score(data[['X1', 'X2']], data['y'])

# svc.predict_proba(data[['X1', 'X2']])返回预测的概率，[:,0]表示预测为负样本的概率
data['Probability'] = svc.predict_proba(data[['X1', 'X2']])[:,0]
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(data['X1'], data['X2'], s=30, c=data['Probability'], cmap='Reds')
plt.show()

可以看到大部分都能正确分类

使用验证数据集选择超参数C和gamma（高斯核函数里的参数）

raw_data = loadmat('data/ex6data3.mat')
X = raw_data['X']
Xval = raw_data['Xval']
y = raw_data['y'].ravel()
yval = raw_data['yval'].ravel()

#设置可选的超参数
C_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]
gamma_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]

#初始化变量
best_score = 0
best_params = {'C': None, 'gamma': None}

# STEP1：遍历每一个超参数
for C in C_values:
    for gamma in gamma_values:
    # STEP2：调用SVM包，计算当前参数下的得分
        svc = svm.SVC(C=C, gamma=gamma)
        svc.fit(X, y)
        score = svc.score(Xval,yval)
        # STEP3：替换得分最高的超参数组合
        if score > best_score:
            best_score = score
            best_params['C'] = C
            best_params['gamma'] = gamma

# (0.965, {'C': 0.3, 'gamma': 100})
best_score, best_params

用SVM来过滤垃圾邮件

spam_train = loadmat('data/spamTrain.mat')
spam_test = loadmat('data/spamTest.mat')
spam_train

# TODO： 获取训练和测试数据，这里应注意把标签y矩阵拉直
X = spam_train['X']
Xtest = spam_test['Xtest']
y = spam_train['y'].ravel()
ytest = spam_test['ytest'].ravel()

# ((4000, 1899), (4000,), (1000, 1899), (1000,))
X.shape, y.shape, Xtest.shape, ytest.shape

svc = svm.SVC(gamma='scale')
svc.fit(X, y)
# Training accuracy = 99.32%
print('Training accuracy = {0}%'.format(np.round(svc.score(X, y) * 100, 2)))

# Test accuracy = 98.7%
print('Test accuracy = {0}%'.format(np.round(svc.score(Xtest, ytest) * 100, 2)))