【深度之眼吴恩达机器学习第四期】笔记(十一)
目录
- 推荐系统
- 基于内容的推荐系统
- 协同过滤
- 均值归一化
- 编程
推荐系统
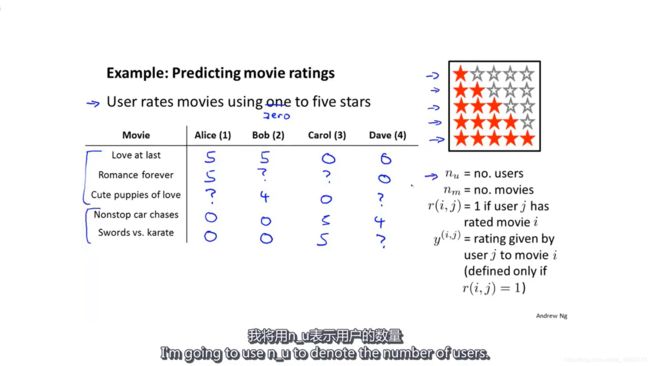
以电影推荐系统为例子,假设4个用户(nu=4)对5部电影(nm=5)作出了以下评分,其中“?”代表第j个用户没有对第i部电影进行评分(r(i,j)=0)。如果第j个用户对第i部电影进行了评分(r(i,j)=1),这时y(i,j)代表用户对电影的评分。
推荐系统要做的,就是在现有评分的基础上,预测“?”的评分,然后把预测评分高的电影推荐给该用户。
基于内容的推荐系统
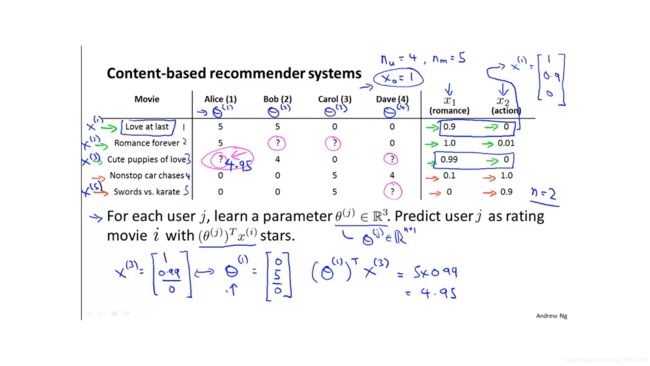
假设现在有用户对电影的评分,也有每部电影的特征。比如第一部电影的特征是X1=[1,0.9,0]T,代表这部电影包含90%的爱情成分,但完全没有包含打斗成分。
基于内容的推荐系统就是用线性回归的方法学习用户的偏好。假设学到某个用户的偏好是θ1=[0,5,0]T,这代表Alice对爱情电影比较感兴趣,而对动作电影完全不感兴趣。
获得了θ1和X3后,就可以对Alice关于第三部电影的评分做出预测(θ1)TX3=4.95,然后根据这个预测的评分判断是否推荐这部电影给Alice。
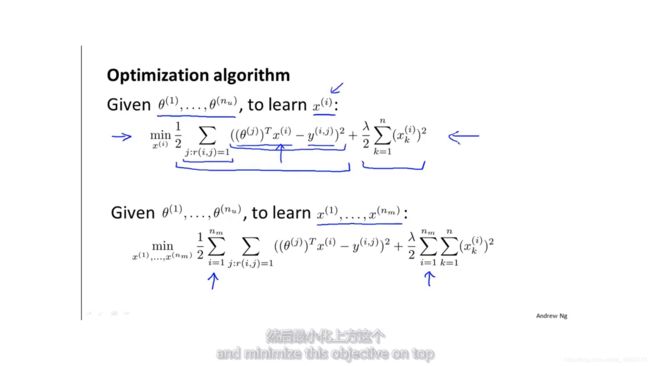
对于第j个用户,要学习的是偏好θj,根据之前的线性回归的知识,学习到的θj要使预测值(θj)TXi和观测值y(i,j)的差距尽可能的小。所以损失函数如下,由于mj是常数,所以去掉并不会影响结果。

然后把所有用户的损失都加起来,整体损失函数如下:

基于内容的推荐系统中的“内容”代表的是电影特征(有多少爱情成分等等),但是在大多数情况下,电影或其他商品的特征并不容易得到,这时候基于内容的推荐系统就不适用了。
协同过滤
协同过滤能够自行学习需要的特征。
假如有用户对各种电影的初始偏好(直接询问用户喜欢什么样的电影),那么就可以用这个初始偏好去学习电影的特征。
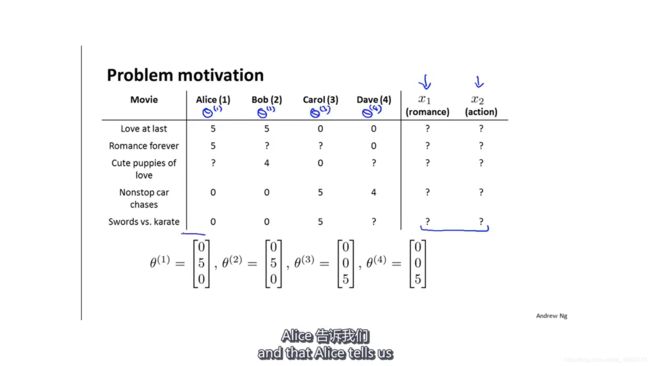
类似于之前的通过电影特征学习用户的偏好,现在可以通过用户的偏好学习电影的特征。
所以,有一组初始用户偏好θ,就可以学习电影特征X。再通过电影特征X优化用户偏好θ,这样迭代,最终算法会收敛到一组电影特征X和一组用户偏好θ。
如果用户都对电影做出了评分,就能帮助系统更好的学习电影特征,从而做出更好的预测。所以协同过滤这个词想要表达的就是用户通过评分帮助系统得到更好的预测结果。

可以把电影评分、电影特征和用户偏好都写成矩阵形式。这样的协同过滤也称为低秩矩阵分解。
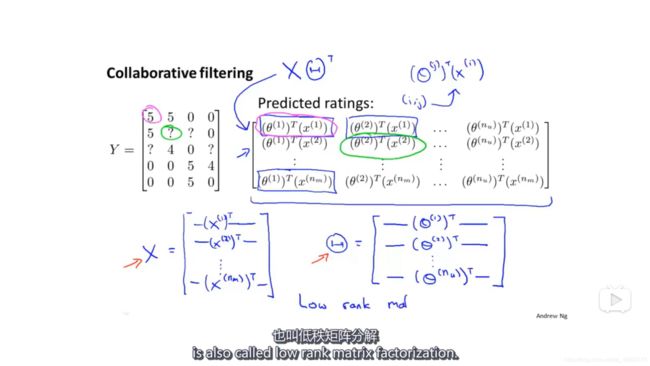
假设已经学习到了所有电影的特征和用户偏好,如果用户表示他喜欢电影i,那么,可以通过二范数来求电影j与电影i的相似程度,然后推荐这些相似电影给用户。
PS.通过协同过滤学习到的电影并不一定有明确的物理意义。

均值归一化
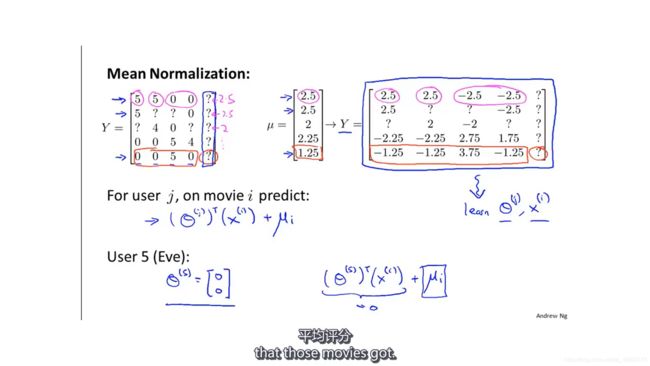
如果有一个新用户Eve,她没有给任何电影评分,那么损失函数的第一项等于0,第二项为常数,要最小化的只有第三项。这时学习到的用户偏好就是θ=[0,0]T。那么对于电影评分的预测就全是0,这对于推荐给她什么电影好并没有任何用处。

均值归一化:
- 计算每部电影的平均分;
- 每个用户对该电影的评分减去该电影的平均分;
- 使用新的评分去训练模型;
- 因为之前减去了平均分,所以在预测的时候要加上平均分。
这时候学习到新用户Eve的偏好依旧是[0,0]T,但是由于加上了平均分,所以对于Eve的预测就是每部电影的平均分。
有人会想,既然如此,为什么不直接预测Eve的评分为电影的平均分?原因是,通过均值归一化的方法可以使所有用户都是用同一种算法,没有例外,不需要单独写个函数预测Eve的评分。
编程
导包并展示数据
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
data = loadmat('data/ex8_movies.mat')
data
# 用户对电影的评分矩阵
Y = data['Y']
# 用户对某部电影是否评分的矩阵,已评分为1,未评分为0
R = data['R']
# ((1682, 943), (1682, 943))
Y.shape, R.shape
# 对第一部电影评分的平均值为3.2061068702290076
Y[1,np.where(R[1,:]==1)[0]].mean()
fig, ax = plt.subplots(figsize=(12,12))
ax.imshow(Y)
ax.set_xlabel('Users')
ax.set_ylabel('Movies')
# 自动调整子图参数(坐标轴标签、刻度标签以及标题的部分),使之填充整个图像区域。
fig.tight_layout()
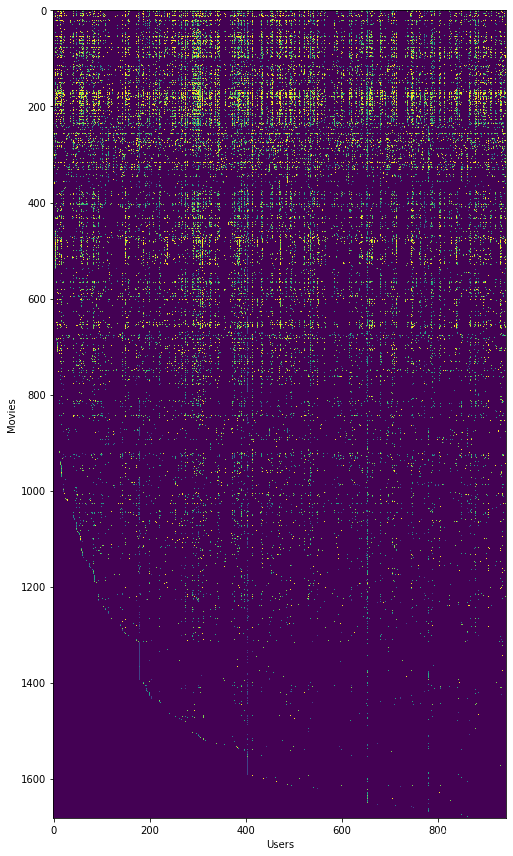
plt.show()Y代表用户对电影的评分(从1到5,0代表没有进行评分)。
R代表用户有没有对某部电影评分,0代表没有评分,1代表有评分。

可以看到Y的最后几行几乎都是黑色的,代表这些电影几乎没有用户对其进行评分。
计算损失和梯度
def cost(params, Y, R, num_features, l):
# INPUT:参数params(也就是X,theta),数据与标签Y,R,特征个数num_features,正则化参数lambda
# OUTPUT:梯度grad,代价函数J
# 初始化变量
Y = np.matrix(Y) # (1682, 943)
R = np.matrix(R) # (1682, 943)
num_movies = Y.shape[0]
num_users = Y.shape[1]
J = 0
X_grad = np.zeros(X.shape)
Theta_grad = np.zeros(Theta.shape)
# 把参数params还原回矩阵的形式
X = np.matrix(np.reshape(params[:num_movies * num_features], (num_movies, num_features)))
Theta = np.matrix(np.reshape(params[num_movies * num_features:], (num_users, num_features)))
# 计算代价函数
error = np.multiply((X * Theta.T) - Y, R)
squared_error = np.power(error, 2)
J = (1. / 2) * np.sum(squared_error)
# 加入正则项
J = J + l*np.sum(np.power(Theta,2))/2
J = J + l*np.sum(np.power(X,2))/2
# 计算包含正则项的梯度
X_grad = error * Theta+l*X
Theta_grad = error.T * X+l*Theta
# 把矩阵拉伸成向量
grad = np.concatenate((np.ravel(X_grad), np.ravel(Theta_grad)))
return J, grad使用少量数据来检查函数是否正确
params_data = loadmat('data/ex8_movieParams.mat')
X = params_data['X']
Theta = params_data['Theta']
# ((1682, 10), (943, 10))
X.shape, Theta.shape
users = 4
movies = 5
features = 3
# 获取数据中的一部分
X_sub = X[:movies, :features]
Theta_sub = Theta[:users, :features]
Y_sub = Y[:movies, :users]
R_sub = R[:movies, :users]
params = np.concatenate((np.ravel(X_sub), np.ravel(Theta_sub)))
J, grad = cost(params, Y_sub, R_sub, features, 1.5)
J, grad
'''(31.34405624427422,
array([ -0.95596339, 6.97535514, -0.10861109, 0.60308088,
2.77421145, 0.25839822, 0.12985616, 4.0898522 ,
-0.89247334, 0.29684395, 1.06300933, 0.66738144,
0.60252677, 4.90185327, -0.19747928, -10.13985478,
2.10136256, -6.76563628, -2.29347024, 0.48244098,
-2.99791422, -0.64787484, -0.71820673, 1.27006666,
1.09289758, -0.40784086, 0.49026541]))'''加载电影标题的数据
movie_idx = {}
f = open('data/movie_ids.txt',encoding= 'gbk')
for line in f:
# line:1 Toy Story (1995)
# tokens:['1', 'Toy', 'Story', '(1995)\n']
tokens = line.split(' ')
# tokens:['1', 'Toy', 'Story', '(1995)']
tokens[-1] = tokens[-1][:-1]
# int(tokens[0]) - 1 = 0
# ' '.join(tokens[1:])='Toy Story (1995)'
movie_idx[int(tokens[0]) - 1] = ' '.join(tokens[1:])
# 'Toy Story (1995)'
movie_idx[0]这是某个新用户对电影的评分
ratings = np.zeros((1682, 1))
ratings[0] = 4
ratings[6] = 3
ratings[11] = 5
ratings[53] = 4
ratings[63] = 5
ratings[65] = 3
ratings[68] = 5
ratings[97] = 2
ratings[182] = 4
ratings[225] = 5
ratings[354] = 5
print('Rated {0} with {1} stars.'.format(movie_idx[0], str(int(ratings[0]))))
print('Rated {0} with {1} stars.'.format(movie_idx[6], str(int(ratings[6]))))
print('Rated {0} with {1} stars.'.format(movie_idx[11], str(int(ratings[11]))))
print('Rated {0} with {1} stars.'.format(movie_idx[53], str(int(ratings[53]))))
print('Rated {0} with {1} stars.'.format(movie_idx[63], str(int(ratings[63]))))
print('Rated {0} with {1} stars.'.format(movie_idx[65], str(int(ratings[65]))))
print('Rated {0} with {1} stars.'.format(movie_idx[68], str(int(ratings[68]))))
print('Rated {0} with {1} stars.'.format(movie_idx[97], str(int(ratings[97]))))
print('Rated {0} with {1} stars.'.format(movie_idx[182], str(int(ratings[182]))))
print('Rated {0} with {1} stars.'.format(movie_idx[225], str(int(ratings[225]))))
print('Rated {0} with {1} stars.'.format(movie_idx[354], str(int(ratings[354]))))
'''Rated Toy Story (1995) with 4 stars.
Rated Twelve Monkeys (1995) with 3 stars.
Rated Usual Suspects, The (1995) with 5 stars.
Rated Outbreak (1995) with 4 stars.
Rated Shawshank Redemption, The (1994) with 5 stars.
Rated While You Were Sleeping (1995) with 3 stars.
Rated Forrest Gump (1994) with 5 stars.
Rated Silence of the Lambs, The (1991) with 2 stars.
Rated Alien (1979) with 4 stars.
Rated Die Hard 2 (1990) with 5 stars.
Rated Sphere (1998) with 5 stars.'''把新用户的数据添加到已有的数据中,原来有943个用户,现在有944个用户。进行均值归一化。
R = data['R']
Y = data['Y']
Y = np.append(Y, ratings, axis=1)
R = np.append(R, ratings != 0, axis=1)
# ((1682, 944), (1682, 944), (1682, 1))
Y.shape, R.shape, ratings.shape
movies = Y.shape[0] # 1682
users = Y.shape[1] # 944
features = 10
learning_rate = 10.
# 随机初始化X和theta
X = np.random.random(size=(movies, features))
Theta = np.random.random(size=(users, features))
params = np.concatenate((np.ravel(X), np.ravel(Theta)))
# ((1682, 10), (944, 10), (26260,))
X.shape, Theta.shape, params.shape
# 均值归一化
Ymean = np.zeros((movies, 1))
Ynorm = np.zeros((movies, users))
for i in range(movies):
# 对于第i部电影,获取评分的下标
idx = np.where(R[i,:] == 1)[0]
# 计算该电影的平均分
Ymean[i] = Y[i,idx].mean()
# 均值归一化
Ynorm[i,idx] = Y[i,idx] - Ymean[i]
# 因为减去均值后,均值约等于0,Ynorm.mean()得到5.5070364565159845e-19是对的
Ynorm.mean()使用均值归一化后的Y训练模型
from scipy.optimize import minimize
fmin = minimize(fun=cost, x0=params, args=(Ynorm, R, features, learning_rate),
method='CG', jac=True, options={'maxiter': 100})
fmin
'''
fun: 38959.17920754673
jac: array([ 0.06997272, 0.06133648, 0.07338806, ..., 0.00534678, -0.00109083, -0.00755571])
message: 'Maximum number of iterations has been exceeded.'
nfev: 152
nit: 100
njev: 152
status: 1
success: False
x: array([ 0.73899214, 0.49007446, 0.33694708, ..., 0.05745608, -0.13162036, 0.06442625])
'''预测分数并给用户推荐电影
# 把向量还原回矩阵
X = np.matrix(np.reshape(fmin.x[:movies * features], (movies, features)))
Theta = np.matrix(np.reshape(fmin.x[movies * features:], (users, features)))
# ((1682, 10), (944, 10))
X.shape, Theta.shape
# 预测电影的评分
predictions = X * Theta.T
# 只计算新加用户的预测
my_preds = predictions[:, -1] + Ymean
# (1682, 1)
my_preds.shape
# 把已经看过的电影排除
mark = ratings==0
my_preds = np.multiply(my_preds,mark)
# np.sort()从上到下是从小到大的,[::-1]表示倒序
sorted_preds = np.sort(my_preds, axis=0)[::-1]
# 找到预测评分最高的10部电影
sorted_preds[:10]
'''
matrix([[5.00000099],
[4.99999988],
[4.99999952],
[4.99999922],
[4.99999884],
[4.99999857],
[4.99999849],
[4.99999834],
[4.99999759],
[4.99999755]])
'''
idx = np.argsort(my_preds, axis=0)[::-1]
idx
'''
Out[47]:matrix([[1188],
[1598],
[1121],
...,
[ 53],
[ 354],
[ 0]], dtype=int64)
'''
print("Top 10 movie predictions:")
for i in range(10):
j = int(idx[i])
print('Predicted rating of {0} for movie {1}.'.format(str(float(my_preds[j])), movie_idx[j]))
'''
Top 10 movie predictions:
Predicted rating of 5.000000993596591 for movie Prefontaine (1997).
Predicted rating of 4.999999875214552 for movie Someone Else's America (1995).
Predicted rating of 4.99999952030098 for movie They Made Me a Criminal (1939).
Predicted rating of 4.999999216853268 for movie Aiqing wansui (1994).
Predicted rating of 4.999998837107815 for movie Saint of Fort Washington, The (1993).
Predicted rating of 4.999998569336983 for movie Great Day in Harlem, A (1994).
Predicted rating of 4.999998494568234 for movie Star Kid (1997).
Predicted rating of 4.999998340436829 for movie Santa with Muscles (1996).
Predicted rating of 4.999997590707319 for movie Entertaining Angels: The Dorothy Day Story (1996).
Predicted rating of 4.9999975535076215 for movie Marlene Dietrich: Shadow and Light (1996) .
'''