刷题计划——双指针算法(二)
209.长度最小的子数组(中等)
题目:
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
输入:s = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
进阶:
如果你已经完成了 O(n) 时间复杂度的解法, 请尝试 O(n log n) 时间复杂度的解法。
同许多寻求子数组或者子串的题目一样,双指针法普遍都可以用来解答这类问题。
首先,此题目的关键是:找出数组中满足其和大于等于s长度的最小连续子数组,意思就是说找到一个总和大于等于s的子数组,该子数组的长度最小。 话不多说,直接上图:

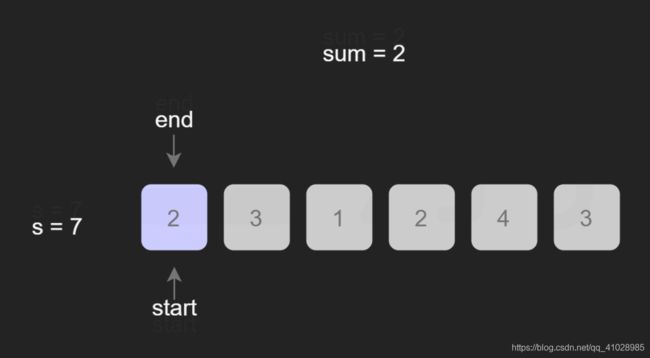

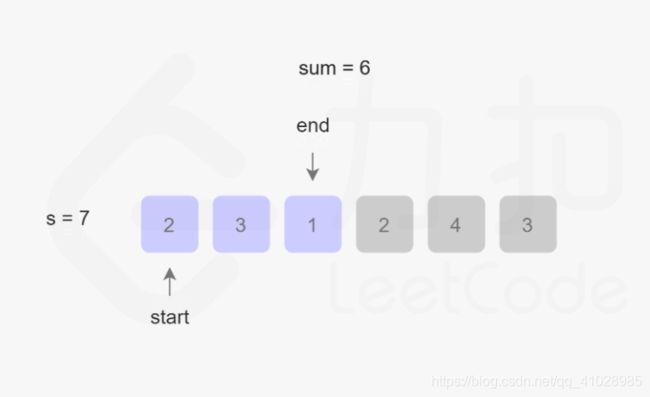
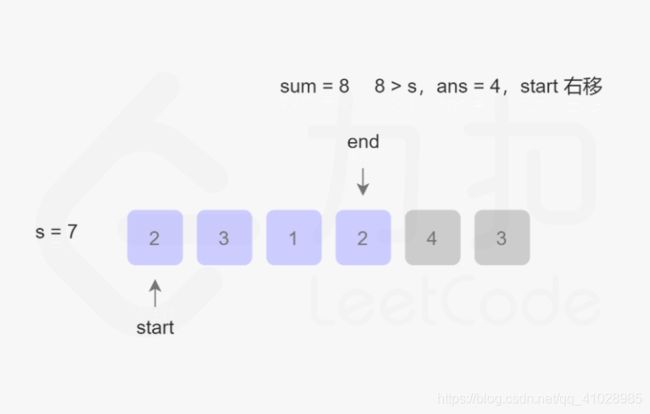
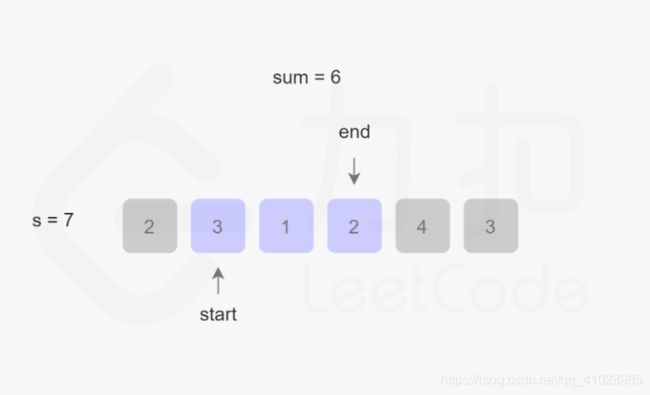
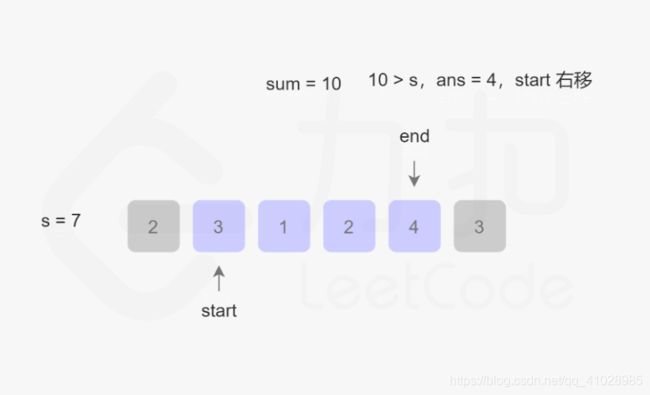
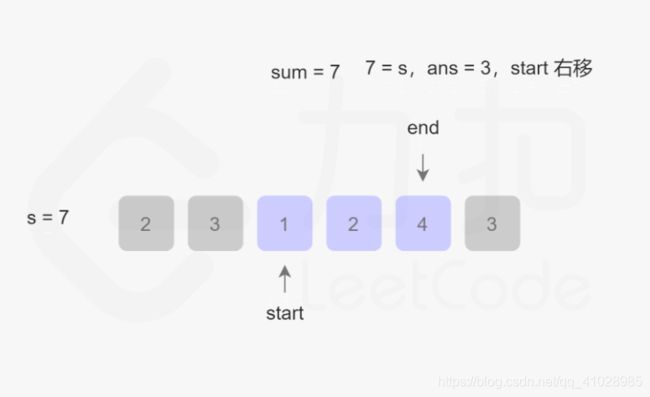
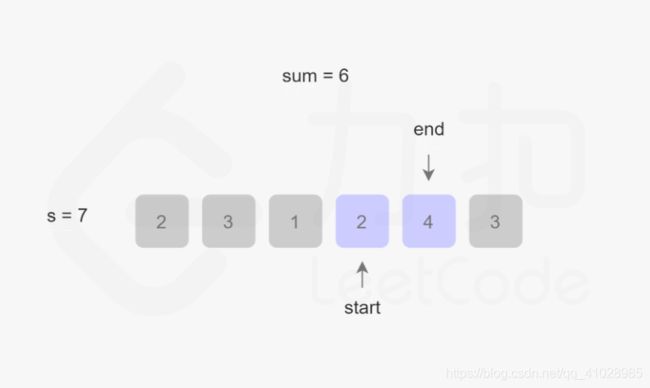
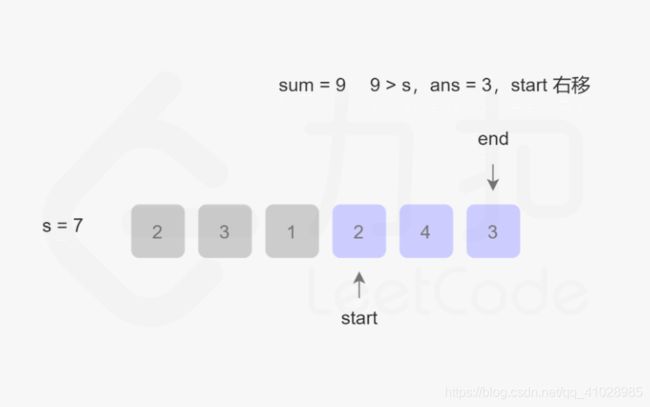
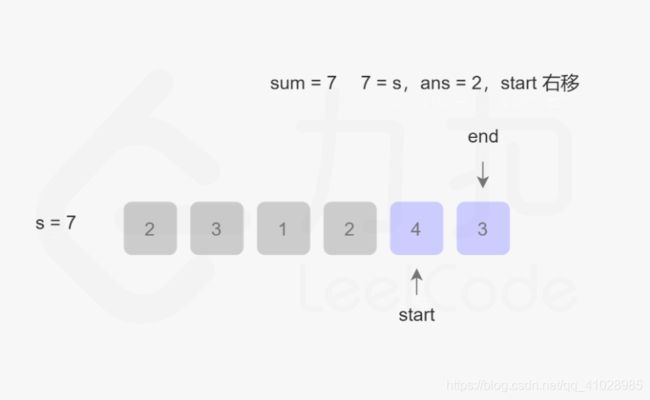
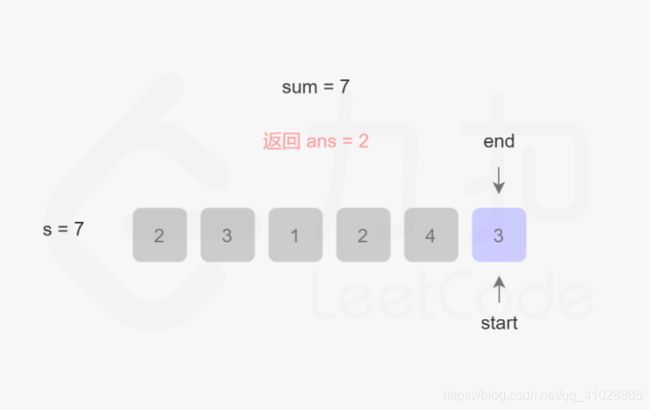
根据图片的演示结果,该算法的最坏事件复杂度为O(2N),最好为O(N),整体事件复杂度为O(N),空间复杂度为O(1)。
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int left = 0, right = 0;
int len = INT_MAX, sum = 0;
while(right < nums.size()){
sum += nums[right];
// 移动左指针,使子数组的大小小于s,方便右指针向前移动
while(sum >= s){
len = min(len, right-left+1);
sum -= nums[left];
left++;
}
right++;
}
// 一旦len的长度没有改变,证明数组中没有符合要求的子数组
return len == INT_MAX? 0: len;
}
};
167. 两数之和 II - 输入有序数组(简单)
题目:
给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。
说明:
返回的下标值(index1 和 index2)不是从零开始的。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
示例:
输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
非常经典的一道双指针类型题目。由题目意思可以知道,题目所要求的是寻找数组中是否存在两个数,其之和等于目标数,并且index1 < index2。
之后,设置左右指针,在数组中寻找是否有符合条件的数,若有则返回Index1 与 index2,若没有则返回空数组。
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int left = 0, right = numbers.size() - 1;
while(left < right){
int tmp = numbers[left] + numbers[right];
if(tmp > target){
right--;
}
else if(tmp < target){
left++;
}
else{
return {left+1, right+1};
}
}
return {};
}
};
当然,由于该数组时升序数组,因此还可以利用升序数组的特性,进行logN级别的查找。
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
for(int i = 0; i < numbers.size(); i++)
{
int l = i + 1, r = numbers.size() - 1;
while(l <= r)
{
int mid = l + ((r - l) >> 1);
if(numbers[mid] + numbers[i] == target)
return {i + 1, mid + 1};
else if(numbers[mid] + numbers[i] < target)
l = mid + 1;
else
r = mid - 1;
}
}
return {};
}
};
763. 划分字母区间(中等)
题目:
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一个字母只会出现在其中的一个片段。返回一个表示每个字符串片段的长度的列表。
示例 1:
输入:S = "ababcbacadefegdehijhklij"
输出:[9,7,8]
解释:
划分结果为 "ababcbaca", "defegde", "hijhklij"。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 的划分是错误的,因为划分的片段数较少。
提示:
S的长度在[1, 500]之间。
S只包含小写字母 'a' 到 'z' 。
在观察子串的结构和题目的要求之后,读者已经大概有一个思路,那就是要得到每一个字符最后出现的位置, 在确定字符最后出现位置之后,在当前遍历的字符的位置与其最后出现的位置之间,就形成了一个“子串”,在这个子串之中的字符,其出现的最后位置就是该子串的最后位置。
可能这么说有些模糊,汇总为三句话:
- 使用哈希表记录每一个字符出现的最后位置;
- 记录当前字符出现的目前位置和最后位置,将该位置设置为一个区间,在此区间之内的字符出现的最后位置就是该子串的最后位置;
- 将该位置添加进res数组中。
class Solution {
public:
vector<int> partitionLabels(string S) {
unordered_map<char, int> _map;
vector<int> res;
int len = S.size();
// 存储每个字母最后出现的位置
for(int i = 0; i < len; i++){
_map[S[i]] = i;
}
int i = 0;
while(i < len){
// 记录当前字母出现的最后位置
int lastPos = _map[S[i]];
// 当前字母出现的目前位置与最后位置之间的字母,其出现的最后位置
for(int j = i+1; j < lastPos; j++){
lastPos = max(lastPos, _map[S[j]]);
}
// lastPos 为该“子串”的最后位置,lastPos-i+1 为该“子串”的长度
res.push_back(lastPos - i + 1);
// 该子串已经确定,直接跳转
i = lastPos + 1;
}
return res;
}
};
234. 回文链表(简单)
题目:
请判断一个链表是否为回文链表。
示例 1:
输入: 1->2
输出: false
示例 2:
输入: 1->2->2->1
输出: true
进阶:
你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
用快慢指针遍历的同时翻转前半部分,然后与后半部分比较即可。
class Solution {
public:
bool isPalindrome(ListNode* head) {
if(!head || !head->next)
return 1;
ListNode *fast = head, *slow = head;
ListNode *p, *pre = NULL;
while(fast && fast->next){
p = slow;
slow = slow->next; //快慢遍历
fast = fast->next->next;
p->next = pre; //翻转
pre = p;
}
if(fast) //奇数个节点时跳过中间节点
slow = slow->next;
while(p){ //前半部分和后半部分比较
if(p->val != slow->val)
return 0;
p = p->next;
slow = slow->next;
}
return 1;
}
};