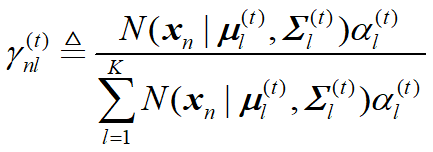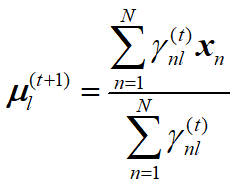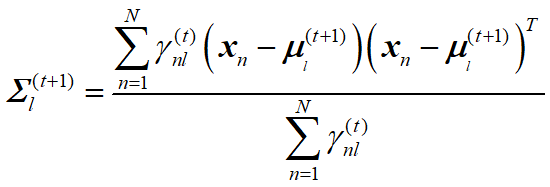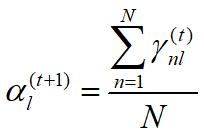EM算法估计GMM （二维高斯混合模型）参数 ｐython 2.7（西瓜书版）

#!/usr/bin/python
# coding:utf-8 
# 19-5-23 上午10:07
# @File    : EM.py
import numpy as np
import math
import matplotlib.pyplot as plt
#real parm
p = [0.2, 0.3, 0.5] #选择高斯分布的概率
mean1 = [1.0, 2.0]
mean2 = [2.0, 1.0]
mean3 = [1.0, 1.0]
cov1 = [[1.0, 0], [0, 10.0]]
cov2 = [[10.0, 0], [0, 1.0]]
cov3 = [[3.0, 0], [0, 4.0]]
# estimate parm
Emean1 = np.array([1.0, 1.0])

Emean2 = np.array([1.0, 1.0])
Emean3 = np.array([1.0, 1.0])
Ecov1 = np.array([[1.0, 0.0], [0.0, 10.0]])
Ecov2 = np.array([[2.0, 0.0], [0.0, 3.0]])
Ecov3 = np.array([[3.0, 0.0], [0.0, 4.0]])
Ep = p = [0.2, 0.3, 0.5]
# saver parameter
# E 步保存的第l 个模型的　R(n,l)
parameter_dict={}
# 分别存放第l 个模型的　R(n,l)
parameter_dict["gama_list1"] = []
parameter_dict["gama_list2"] = []
parameter_dict["gama_list3"] = []

def DenityOfNorm(Data, Emean,Ecov):
    # return 　EM估计参数　下　data (x, y)处　的正态函数密度
    # Data 输入的数据的点
    #Emean ,EM算法估计的参数
    #Ecov ,EM在第t步估计的协方差矩阵
    #
    # print Ecov.shape
    #
    Ecov_sqrt = math.sqrt(np.linalg.det(Ecov)) #协方差矩阵行列式值的开平方
    Ecov_inv = np.linalg.inv(Ecov) #协方差矩阵的逆
    #we
    Data =np.reshape(Data,[2,1])
    Emean =np.reshape(Emean,[2,1])
    Minus_Data = Data - Emean
    Minus_Data_T = Minus_Data.T
    res = (1.0 / (2.0 * math.pi * Ecov_sqrt)) * math.exp(
        (-0.5) * (np.dot(np.dot(Minus_Data_T, Ecov_inv), Minus_Data)))
    return res
    # sigma_sqrt = math.sqrt(np.linalg.det(sigma))  # 协方差矩阵绝对值的1/2次
    # sigma_inv = np.l

#　生成二维高斯模型的数据
def ini_Normal(mean, cov):
    # 返回一个由size指定形状的数组，数组中的值服从
    # μ = loc, σ = scale
    data =np.random.multivariate_normal(mean, cov,1)
    return data

#生成高斯混合模型的数据
def ini_data(k=1,parm1=0.2,parm2=0.3):
    data= []
    for i in range(k):
        d = np.random.rand(1)
        if d < parm1:
            data.append(ini_Normal(mean1, cov1))
        elif d < parm1+parm2:
            data.append(ini_Normal(mean2, cov2))
        else:
            data.append(ini_Normal(mean3, cov3))
    return data

#第Ｅ步
def E(Data):
    # !!!!!!!!!!!!!!!!
    # 这里一定要清空，　不然会很尴尬，　之前第三个忘了清空，以为陷入局部最优值，检查了很久
    # !!!!!!!!!!!!!!!
    global parameter_dict
    parameter_dict["gama_list1"] = []
    parameter_dict["gama_list2"] = []
    parameter_dict["gama_list3"] = []
    for point in Data:
        # gama_i = (pw * PDF(point, mu_2, sigma_2)) / (
        #         (1.0 - pw) * PDF(point, mu_1, sigma_1) + pw * PDF(point, mu_2, sigma_2))
        # parameter_dict["gama_list"].append(gama_i)
        gam_sum = Ep[0] * DenityOfNorm(point,Emean1,Ecov1)+Ep[1] * DenityOfNorm(point,Emean2,Ecov2)+Ep[2] * DenityOfNorm(point,Emean3,Ecov3)
        gam1_i = Ep[0] * DenityOfNorm(point,Emean1,Ecov1) / gam_sum
        parameter_dict["gama_list1"].append(gam1_i)
        gam2_i = Ep[1] * DenityOfNorm(point,Emean2, Ecov2) / gam_sum
        parameter_dict["gama_list2"].append(gam2_i)
        parameter_dict["gama_list3"].append(1.0-gam2_i-gam1_i)

#第Ｍ步
def M(Data):
    r1 = 0
    r2 = 0
    r3 = 0
    for i in range(len(parameter_dict['gama_list2'])):
        r1 = r1 + parameter_dict["gama_list1"][i]
        r2 = r2 + parameter_dict["gama_list2"][i]
        r3 = r3 + parameter_dict["gama_list3"][i]
        # r3 += 1- parameter_dict["gama_list1"][i]- parameter_dict["gama_list2"][i]
    # updata estimated p
    # for i in range(3):
    Ep[0] = r1 / len(Data)
    Ep[1] = r2 / len(Data)
    Ep[2] = r3 / len(Data)

    # updata estimated mean
    Emean1_new= np.array([0.0, 0.0])
    Emean2_new= np.array([0.0, 0.0])
    Emean3_new= np.array([0.0, 0.0])
    #
    Emean1_new.shape = (1,2)
    Emean2_new.shape = (1,2)
    Emean3_new.shape = (1,2)
    # print parameter_dict["gama_list1"].shape
    for i in range(len(Data)):
        print i
        # print parameter_dict["gama_list1"][i]
        Emean1_new =Emean1_new + Data[i] * parameter_dict["gama_list1"][i] /r1
        Emean2_new =Emean2_new + Data[i] * parameter_dict["gama_list2"][i] /r2
        Emean3_new =Emean3_new + Data[i] * parameter_dict["gama_list3"][i] /r3
        # Emean3_new += Data[i] * (1-parameter_dict["gama_list1"][i]-parameter_dict["gama_list2"])
    global Emean1
    global Emean2
    global Emean3
    # print "---------------------------------------"
    # print Emean1_new.shape
    Emean1 = Emean1_new
    Emean2 = Emean2_new
    Emean3 = Emean3_new


    # updata estimated cov

    Ecov1_new = np.array([[0, 0], [0, 0]])
    Ecov2_new = np.array([[0, 0], [0, 0]])
    Ecov3_new = np.array([[0, 0], [0, 0]])
    for i in range(len(Data)):
        Data_MiuMean1 = Data[i] - Emean1
        Data_MiuMean2 = Data[i] - Emean2
        Data_MiuMean3 = Data[i] - Emean3
        Data_MiuMean1_T = np.array(Data_MiuMean1).T
        Data_MiuMean2_T = np.array(Data_MiuMean2).T
        Data_MiuMean3_T = np.array(Data_MiuMean3).T
        # 测试
        # MYtry = np.dot(Data_MiuMean2,Data_MiuMean2_T)
        # MYtry1 = np.dot(Data_MiuMean2_T,Data_MiuMean2)
        # print MYtry, MYtry.shape
        # print MYtry1, MYtry1.shape
        #

        Ecov1_new = Ecov1_new + np.dot(Data_MiuMean1_T, Data_MiuMean1) * parameter_dict["gama_list1"][i]
        Ecov2_new = Ecov2_new + np.dot(Data_MiuMean2_T, Data_MiuMean2) * parameter_dict["gama_list2"][i]
        Ecov3_new = Ecov3_new + np.dot(Data_MiuMean3_T, Data_MiuMean3) * parameter_dict["gama_list3"][i]
        # Ecov2_new = Ecov2_new + np.d
    global Ecov1
    global Ecov2
    global Ecov3
    # print "------------------------"
    # print Ecov1_new.shape
    Ecov1 = Ecov1_new / r1
    Ecov2 = Ecov2_new / r2
    Ecov3 = Ecov3_new / r3

#不可以控制迭代次数ＥM算法
def EM_iterate( Data, esp=0.0001):


    # Data:数据
    #param esp:终止约束，第n次优化和第ｎ＋１次优化差距小于0.0001

    # set_parameter(mu_1, sigma_1, mu_2, sigma_2, pi_weight)
     while (True):
         old_m1 = Emean1
         old_m2 = Emean2
         old_m3 = Emean3
         E(Data)
         M(Data)
         #
         # print Emean2.shape
         #
         delta_1 = Emean1 - old_m1
         delta_2 = Emean2 - old_m2
         delta_3 = Emean3 - old_m3
         # print delta_1 ,delta_1.shape
         # delta_2 = E - old_m2
         if math.fabs(delta_1[0][0]) < esp and math.fabs(delta_1[0][1]) < esp and math.fabs(
                 delta_2[0][0]) < esp and math.fabs(delta_2[0][1]) < esp and math.fabs(
             delta_3[0][0]) < esp and math.fabs(delta_3[0][1]) < esp:
             break

#EM 算法可以控制迭代次数
def EM_iterat_N(iterm, Data,esp=0.0001):
    #　记录更新的过程
    mean1_trace = [[], []]
    mean2_trace = [[], []]
    mean3_trace = [[], []]
    # mean2_trace = [[], []]
    # mean3_trace = [[], []]
    for i in range(iterm):
            old_m1 = Emean1
            old_m2 = Emean2
            old_m3 = Emean3
            E(Data)
            M(Data)
            #
            # print Emean2.shape
            #
            mean1_trace[0].append(Emean1[0][0])
            mean1_trace[1].append(Emean1[0][1])
            mean2_trace[0].append(Emean2[0][0])
            mean2_trace[1].append(Emean2[0][1])
            mean3_trace[0].append(Emean3[0][0])
            mean3_trace[1].append(Emean3[0][1])
            delta_1 = Emean1 - old_m1
            delta_2 = Emean2 - old_m2
            delta_3 = Emean3 - old_m3
            # print delta_1 ,delta_1.shape
            # delta_2 = E - old_m2
            if math.fabs(delta_1[0][0]) < esp and math.fabs(delta_1[0][1]) < esp and math.fabs(delta_2[0][0]) < esp and math.fabs(delta_2[0][1]) < esp and math.fabs(delta_3[0][0]) < esp and math.fabs(delta_3[0][1]) < esp:
                break
    # print mean1_trace
    # plt.subplot(121)
    # plt.xlim(xmax=5, xmin=2)
    # plt.ylim(ymax=90, ymin=60)
    # plt.xlabel("eruptions")
    # plt.ylabel("waiting")
    # plt.plot(mean1_trace[:,0], mean1_trace[:,1], 'r-')
    # plt.plot(mean1_trace[:,0],mean1_trace[:,1], 'b^')
    #
    # plt.subplot(122)
    # plt.xlim(xmax=4, xmin=0)
    # plt.ylim(ymax=60, ymin=40)
    # plt.xlabel("eruptions")
    # plt.ylabel("waiting")
    # plt.plot(mean2_trace[:,0], mean2_trace[:,1], 'r-')
    # plt.plot(mean2_trace[:,0], mean2_trace[:,1], 'bo')
    # plt.show()
    return mean1_trace,mean2_trace,mean3_trace

def main():
    # data = gen_clusters()
    # save_data(data, '3clusters.txt')
    # d = load_data('3clusters.txt')
    # show_scatter(d)
    # # show_scatter(d)
    data = ini_data(10000)
    #print data
    Emean1.shape = (1,2)
    Emean2.shape = (1,2)
    Emean3.shape = (1,2)
    # EM_iterate( data)
    trace1,trace2,trace3 = EM_iterat_N(50, data)
    # 画图
    plt.subplot(131)
    plt.xlim(xmax=5, xmin=2)
    plt.ylim(ymax=90, ymin=60)
    plt.xlabel("Emean1_x")
    plt.ylabel("Emean1_y")
    plt.plot(trace1[0], trace1[1], 'r-')
    plt.plot(trace1[0], trace1[1], 'b^')
    plt.axis('tight')

    plt.subplot(132)
    plt.xlim(xmax=4, xmin=0)
    plt.ylim(ymax=60, ymin=40)
    plt.xlabel("Emean2_x")
    plt.ylabel("Emean2_y")
    plt.plot(trace2[0], trace2[1], 'r-')
    plt.plot(trace2[0], trace2[1], 'bo')
    plt.axis('tight')

    plt.subplot(133)
    plt.xlim(xmax=4, xmin=0)
    plt.ylim(ymax=60, ymin=40)
    plt.xlabel("Emean3_x")
    plt.ylabel("Emean3_y")
    plt.plot(trace3[0], trace3[1], 'r-')
    plt.plot(trace3[0], trace3[1], 'bv')
    plt.axis('tight')
    plt.show()

    print "real mean1: ", mean1
    print "real mean1: ", mean2
    print "real mean1: ", mean3
    print "estimate means:", Emean1, Emean2, Emean3

if __name__ == '__main__':
    main()

 更新公式：