SDOI2017 总结
文章目录
- 4948【SDOI2017】数字表格
- 4949【SDOI2017】树点涂色
- 4950【SDOI2017】序列计数
- 4954【SDOI2017】新生舞会
- 4956【SDOI2017】相关分析
- 5417【SDOI2017】切树游戏
4948【SDOI2017】数字表格
莫比乌斯反演+数论分块

括号里面的部分 O ( n ⋅ l n n ) O(n\cdot lnn) O(n⋅lnn)暴力维护(每个数更新自己倍数)
4949【SDOI2017】树点涂色
l c t lct lct+线段树维护子树
操作1即为 A c c e s s Access Access
考虑答案的定义,可以改为: x x x到根经过的虚边数量
初始化每个点的值为它的深度, f [ x ] = d e p [ x ] f[x]=dep[x] f[x]=dep[x]
然后 A c c e s s Access Access的时候,原来的右儿子的子树全部 + 1 +1 +1(变虚为实),新的右儿子子树全部 − 1 -1 −1(变实为虚),维护子树用 d f s dfs dfs序+线段树区间加即可
操作2用容斥, f ( u ) + f ( v ) − 2 ⋅ f ( l c a ) f(u)+f(v)-2\cdot f(lca) f(u)+f(v)−2⋅f(lca)
操作3线段树维护区间 m a x max max
4950【SDOI2017】序列计数
容斥,方案=总方案-不含质数方案
计算方案考虑多项式卷积
设生成函数 F ( n ) = f ( n ) x n F(n)=f(n)x^n F(n)=f(n)xn, f ( n ) f(n) f(n)表示和膜 p p p余 n n n的方案数
初始化 F : F: F:for(1->m)f(i%p)++
总方案数相当于求 F F F的 n n n次方
不含质数的方案就令 f ( P r i m e % p ) − − f(Prime\%p)-- f(Prime%p)−−重新算一遍即可
两次快速幂套多项式循环卷积即可
4954【SDOI2017】新生舞会
分数规划+ K M KM KM
二分 m i d mid mid,设定 v a l [ i ] [ j ] = a [ i ] [ j ] − m i d ⋅ b [ i ] [ j ] val[i][j]=a[i][j]-mid\cdot b[i][j] val[i][j]=a[i][j]−mid⋅b[i][j],跑 K M KM KM
- a n s ≥ 0 ans\geq0 ans≥0,说明有更大的答案 h e a d = m i d head=mid head=mid
- e l s e else else, t a i l = m i d tail=mid tail=mid
4956【SDOI2017】相关分析
线段树

维护 ∑ x i \sum x_i ∑xi, ∑ y i \sum y_i ∑yi, ∑ x i y i \sum x_iy_i ∑xiyi, ∑ x i 2 \sum x_i^2 ∑xi2
对于 3 3 3操作,转化成区间覆盖和区间加两个操作
覆盖的时候,令 x i = y i = i x_i=y_i=i xi=yi=i运用 ∑ 1 n i \sum_1^ni ∑1ni和 ∑ 1 n i 2 \sum_1^ni^2 ∑1ni2的两个公式去直接计算
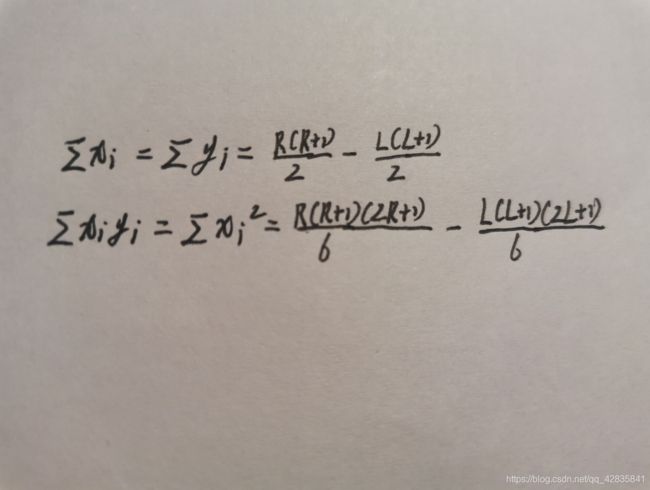
5417【SDOI2017】切树游戏
题意:两个操作
- 求树上异或和为 k k k的连通块个数
- 修改点权
考虑静态朴素 d p : dp: dp:
设 f [ x ] [ k ] f[x][k] f[x][k]表示以 x x x为顶点,异或和为 k k k的连通块个数
a n s [ x ] [ k ] ans[x][k] ans[x][k]表示 x x x子树内,异或和为 k k k的连通块个数
枚举儿子 s o n son son:
-
f [ x ] [ k ] + = ∑ i ⨁ j = = k f [ x ] [ i ] ⋅ f [ s o n ] [ j ] f[x][k] +=\sum_{i\bigoplus j==k}f[x][i]\cdot f[son][j] f[x][k]+=∑i⨁j==kf[x][i]⋅f[son][j]
( v a l [ x ] val[x] val[x]为初始值,第 a [ x ] a[x] a[x]项为 1 1 1,其余项为 0 0 0)
-
a n s [ x ] [ k ] + = a n s [ s o n ] [ k ] ans[x][k]+=ans[son][k] ans[x][k]+=ans[son][k]
对于第一个式子,考虑使用 f w t fwt fwt把卷积转化成乘积,那么对于一个儿子
-
F [ x ] [ k ] = F [ x ] [ k ] ⋅ F [ s o n ] [ k ] + F [ x ] [ k ] = F [ x ] [ k ] ⋅ ( F [ s o n ] [ k ] + 1 ) F[x][k]=F[x][k]\cdot F[son][k]+F[x][k]=F[x][k]\cdot (F[son][k]+1) F[x][k]=F[x][k]⋅F[son][k]+F[x][k]=F[x][k]⋅(F[son][k]+1)
-
A n s [ x ] [ k ] = A n s [ x ] [ k ] + A n s [ s o n ] [ k ] Ans[x][k]=Ans[x][k]+Ans[son][k] Ans[x][k]=Ans[x][k]+Ans[son][k]
所以
-
F [ x ] [ k ] = V a l [ x ] [ k ] ⋅ Π s o n ( F [ s o n ] [ k ] + 1 ) F[x][k]=Val[x][k]\cdot \Pi_{son}(F[son][k]+1) F[x][k]=Val[x][k]⋅Πson(F[son][k]+1)
-
A n s [ x ] [ k ] = F [ x ] [ k ] + ∑ s o n A n s [ s o n ] [ k ] Ans[x][k]=F[x][k]+\sum_{son} Ans[son][k] Ans[x][k]=F[x][k]+∑sonAns[son][k]
由于要支持修改,继续优化,考虑动态 d p dp dp
令 g F [ x ] [ k ] = v a l [ x ] [ k ] ⋅ Π 轻 儿 子 ( F [ s o n ] [ k ] + 1 ) gF[x][k]=val[x][k]\cdot \Pi_{轻儿子}(F[son][k]+1) gF[x][k]=val[x][k]⋅Π轻儿子(F[son][k]+1), g A n s [ x ] [ k ] = ∑ 轻 儿 子 A n s [ s o n ] [ k ] gAns[x][k]=\sum_{轻儿子}Ans[son][k] gAns[x][k]=∑轻儿子Ans[son][k]
则
-
F [ x ] [ k ] = ( F [ 重 儿 子 ] [ k ] + 1 ) ⋅ g F [ x ] [ k ] F[x][k]=(F[重儿子][k]+1)\cdot gF[x][k] F[x][k]=(F[重儿子][k]+1)⋅gF[x][k]
= F [ 重 儿 子 ] [ k ] ⋅ g F [ x ] [ k ] + g F [ x ] [ k ] =F[重儿子][k]\cdot gF[x][k]+gF[x][k] =F[重儿子][k]⋅gF[x][k]+gF[x][k]
-
A n s [ x ] [ k ] = A n s [ 重 儿 子 ] [ k ] + g A n s [ x ] [ k ] + F [ x ] [ k ] Ans[x][k]=Ans[重儿子][k]+gAns[x][k]+F[x][k] Ans[x][k]=Ans[重儿子][k]+gAns[x][k]+F[x][k]
= A n s [ 重 儿 子 ] [ k ] + g A n s [ x ] [ k ] + F [ 重 儿 子 ] [ k ] ⋅ g F [ x ] [ k ] + g F [ x ] [ k ] =Ans[重儿子][k]+gAns[x][k]+F[重儿子][k]\cdot gF[x][k]+gF[x][k] =Ans[重儿子][k]+gAns[x][k]+F[重儿子][k]⋅gF[x][k]+gF[x][k]
构造出矩阵:
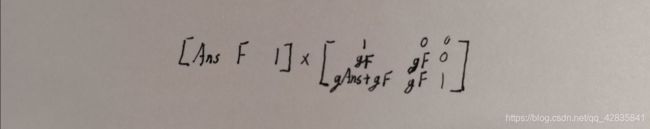
然后就是动态 d p dp dp的套路,维护重链的乘积,修改的时候沿重链往上跳,每次更新 g g g便消去旧的贡献,增添新的贡献
gF/=(prev_F+1); gF*=(now_F+1)gAns-=prev_Ans; gAns+=now_Ans
还有一点, p r e v F + 1 prev_F+1 prevF+1可能是 10007 10007 10007的倍数,然后导致 g F gF gF变成 0 0 0,这个时候 0 / 0 = ? ? ? 0/0=??? 0/0=???
所以另外记录一个 z e r o _ c n t zero\_cnt zero_cnt数组记录 g F gF gF中有多少个 0 0 0,更新的时候同时维护一下即可(如果 z e r o _ c n t [ x ] > 0 zero\_cnt[x]>0 zero_cnt[x]>0,那么 g F = 0 gF=0 gF=0)
gF*=(F+1)->if((F+1)%MOD==0)zero_cnt++; else gF*=(F+1);gF/=(F+1)->if((F+1)%MOD==0)zero_cnt--; else gF/=(F+1)a[][]=gF->if(zero_cnt>0)a[][]=0; else a[][]=gF
然后还有一点,我线段树会 M L E MLE MLE,要用全局平衡二叉树?