算法总结
本文仅供自己复习使用
1、五大基本算法
写在前面:
a、凡是用到递归,就画递归树
1)分治算法
具体来讲就是分而治之,把一个大问题分成很多相同或相似的小问题,小问题再分,直到无法再分,所有小问题的结果合起来就是最终结果
常见的有排序中的快速排序和归并排序,分治经常和递归一起提及
①分治适合的情况
a、该问题缩小到一定规模就可以解决
b、该问题可以分成若干小问题
c、该问题若干小问题的解可以合并成这个问题的答案
d、该问题分出来的若干小问题都是独立的
若满足a、b,却不满足c,可以考虑贪心算法或者动态规划算法
若不满足d方法,可以考虑一下动态规划算法(这样效率更高)
②关于分治的经典问题
a、二分搜索
前提是有序数组
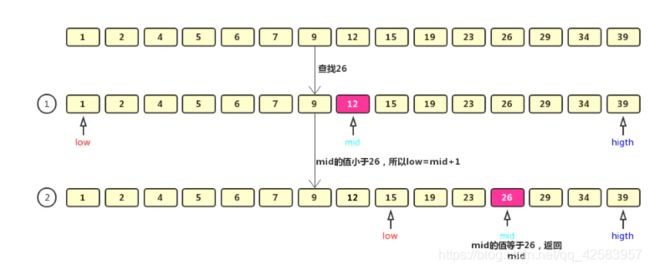
递归情况:
function binarySearch(arr, num, left = 0, right = arr.length - 1) {
if(left > right) {
return -1
}
let middle = Math.floor((left + right) / 2)
if(arr[middle] > num) {
right = middle - 1
} else if(arr[middle] < num) {
left = middle + 1
} else {
return middle
}
return binarySearch(arr, num, left, right)
}
非递归情况:
function binarySearch(arr, num) {
let left = 0;
let right = arr.length - 1;
while(left <= right) {
let middle = Math.floor((left + right) / 2)
if(arr[middle] > num) {
right = middle - 1
} else if(arr[middle] < num) {
left = middle + 1
} else {
return middle
}
}
return -1
}
深入讲解一下!!!
模板
function binarySearch(arr, value) {
let left = 0,right = arr.length - 1
while(...) {
// 这里使用 left + (right - left) / 2
// 而不是使用 (left + right) / 2
// 是因为 left + right 有可能超过 Number.MAX_VALUE
let mid = left + Math.ceil((right - left) / 2)
if(arr[mid] > value) {
right = ...
} else if(arr[mid] < value) {
left = ...
} else if(arr[mid] === value) {
...
}
}
return ...
}
这个模板的重点就是用 else-if 而不是 else,这样就能很简单看出逻辑
而 … 就是填充一些具体代码的地方
查找一个数(基本的二分搜索)
function binarySearch(arr, value) {
let left = 0; right = arr.length - 1
// ①
while(left <= right) {
let mid = left + Math.ceil((right - left) / 2)
if(arr[mid] === value) {
return mid
} else if(arr[mid] > value) {
// ②
right = mid - 1
} else if(arr[mid] < value) {
// ②
left = mid + 1
}
}
return -1
}
问题①:为啥用 left <= right,left < right 不行吗.
left <= right 是对闭区间([left, right])也就是初始的时候 right = arr.length - 1 来说的,再具体一点,他的终止条件为[right + 1, right],举个例子就是[3, 2]
而 left < right 是对左闭右开([left, right))也就是初始的时候是 right = arr.length 来说的,终止条件为[right, right],即【2, 2】
但是正经的终止条件应当是区间为空,而第二种很明显,还有一个数 arr[right]
所以如果是第二种写法,就应该改一下
function binarySearch2(arr, value) {
let left = 0, right = arr.length;
while(left < right) {
let mid = left + Math.ceil((right - left) / 2)
if(arr[mid] > value) {
right = mid - 1
} else if(arr[mid] < value) {
left = mid + 1
} else if (arr[mid] === value) {
return mid
}
}
// 这个时候出来的left = right,而left这个值没有和value比较过
return arr[left] === value ? left : -1
}
问题②:为什么用 left = mid + 1, right = mid - 1 而不是用 left = mid, right = mid
因为我们之前搜索都是闭区间嘛,[left, right],如果mid不是,那么就不需要在mid上浪费,所以是 mid + 1 或者 mid - 1
问题③:该算法的缺点
这个算法是无法对一个数组中有两个相同的数进行搜索的,如1,2,2,3,4,5,就不一定能找到第一个2
b、大整数乘法
首先,有些语言不支持存入很多位的整数,且乘法远比加法的速度慢,而这里的数的前提是位数很多,所以我们可以采取分治来做大整数相乘
假设做 8132579076 * 921352184
我们可以思考把这两个整数各自拆成两部分
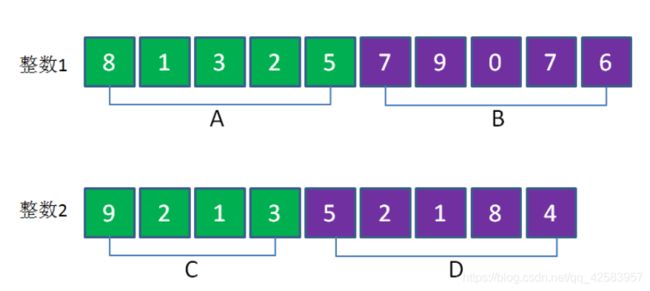
从高到低,把两个整数都平分(这里往下取,所以是Math.floor,Math.ceil是向上取整),得到ABCD四块
然后我们可以得到第一种,也就是当两个整数位数都相等的时候
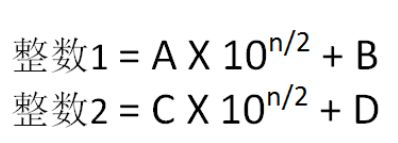
这样一来,两个整数的乘积可以转为
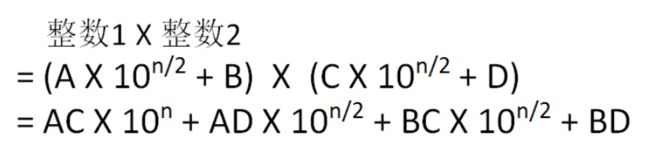
这样的话其实计算AC、AD、BC、BD即可,同理,继续往下分,直到我们拿的整数只有一位就很好计算了,但这个时候有四次乘法,三次加法,我们仍然可以找到简便方法,下面会说
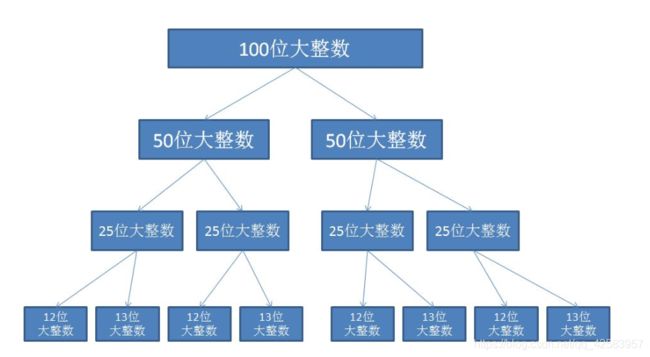
当然,我们也可以运用数学方法,得到一个更简单的方法:
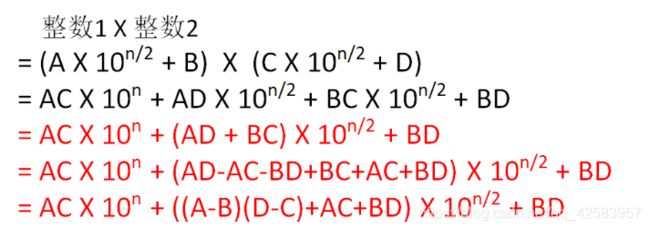
这样,我们就只需要求得三次乘法,四次加法即可
而如果两个整数位数不相等,就不能把位数都笼统地归为 n / 2,而且还有个问题就是这里的 n / 2 因为使用了 Math.floor() 会向下取整,所以真正的 n / 2 = nums.length - Math.floor(nums.length / 2),m / 2 也同理
然后看A大不大,A不大就直接乘以C,否则A和C继续,AD,BC,BD也是
c、棋盘覆盖
在一个2k×2k 个方格组成的棋盘中,恰有一个方格与其它方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。
在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,
且任何2个L型骨牌不得重叠覆盖。
![]()
分析:
我们可以使用分治的方法把2k棋盘往下分,分成4个子棋盘,然后一直分,直到找到某个 2*2 的棋盘中有这个特殊的方格,然后把这个 2*2 的棋盘的其他三格用L型特殊棋子覆盖即可,这样剩下的棋盘就一定可以被填满
d、归并排序
假设有一个数列,10, 4, 6, 3, 8, 2, 5, 7,做归并排序

如图,首先要这样慢慢分开,然后要再把他们都合并在一起
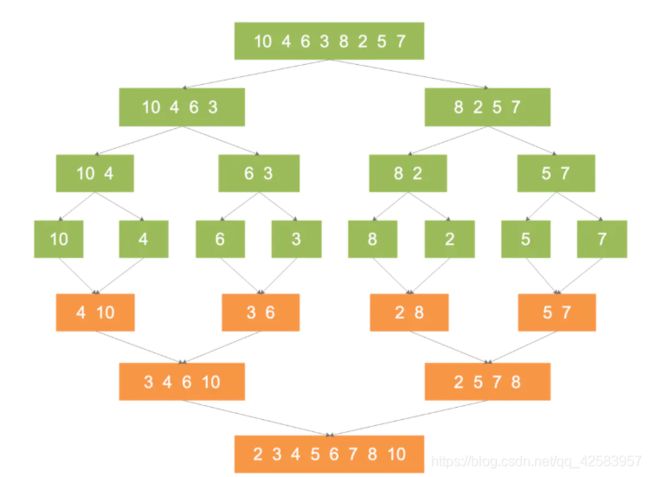
所以总结就两步,一分成小问题(分),二合并成最终问题(治)
function mergeSort(arr) {
// 如果这个数组只有一个或没有就停止迭代,把自己返回出去
if(arr.length <= 1) {
return arr;
}
// 拿到中间
let mid = Math.floor(arr.length / 2)
// 得到左边(slice包含begin,不包含end),不改变原数组
let left = mergeSort(arr.slice(0, mid));
// 右边
let right = mergeSort(arr.slice(mid))
let res = sort(left, right)
return res;
}
function sort(left, right) {
let res = []
// 如果两边都有数据就比大小
while(left.length && right.length) {
if(left[0] < right[0]) {
res.push(left.shift())
} else {
res.push(right.shift())
}
}
// 如果左边没了
while(right.length) {
res.push(right.shift())
}
// 如果右边没了
while(left.length) {
res.push(left.shift())
}
return res;
}
归并的时间复杂度为O(nlogN)
e、快速排序
归并排序是一分二,而快排不是,快排是找一个标杆,让小的在左边,大的在右边,先局部有序,再最终有序
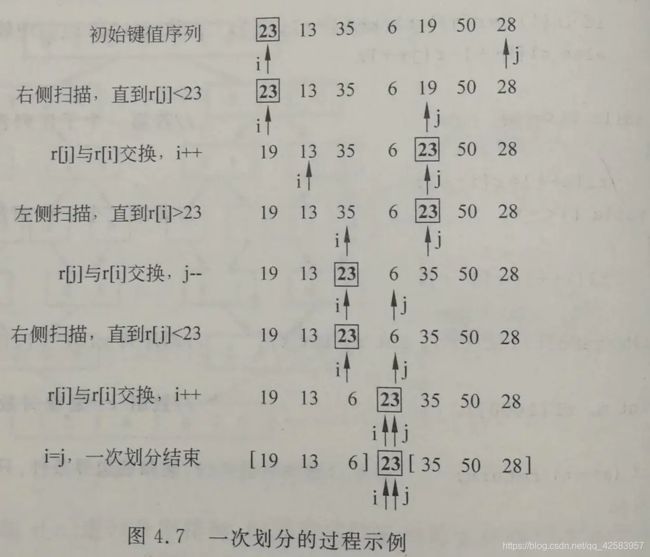
function quickSort(arr, left=0, right=arr.length - 1) {
// 递归终止条件为只要左边大于等于右边就行
if(left >= right) return;
// 获取中间值
let index = partition(arr, left, right);
// 左边的继续
quickSort(arr, left, index - 1)
// 右边的继续
quickSort(arr, index + 1, right)
return arr;
}
function partition(arr, left, right) {
// 基准这里使用第一个
let pivot = left;
while(left < right) {
// 循环,直到找到小于基准的
while(arr[right] >= arr[pivot] && left < right) {
right--;
}
// 通过循环找到左边大于基准的
while(arr[left] <= arr[pivot] && left < right) {
left++;
}
// 将两个交换
swap(arr, left, right)
}
// 此时left=right,让这个值和基准交换
swap(arr, pivot, left)
return left;
}
function swap(arr, left, right) {
let temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
快速排序是不稳定的算法,时间复杂度为O(nlogn)
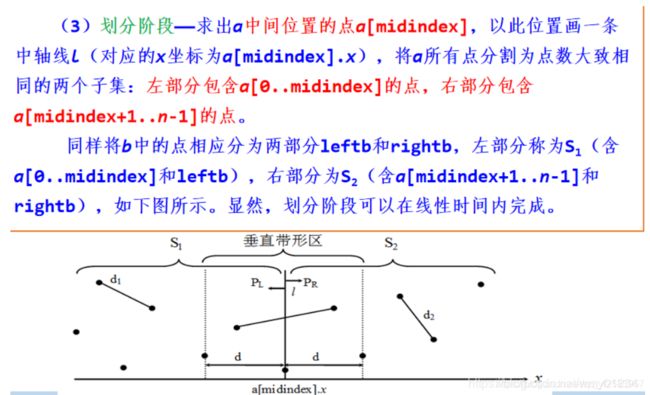
f、最接近点对问题
给定平面上n个点,找出其中的一对点的距离,使得在这n个点的所有点对中,该距离为所有点对中最小的
思路:
1、先根据x排序,找到中间的那个点
2、把区域分成左边和右边,递归地找到左边最小的距离d1,以及右边最下的距离d2,在d1和d2中找到最小的距离作为d,然后以中线为轴向两边各取d距离,被框住的点,挨个求最小的距离d3,然后与d比较
function getPoint(arr) {
// 先处理点
arr = arr.map(res => {
let xy = res.split(' ');
return {x: parseFloat(xy[0]), y: parseFloat(xy[1])}
})
// 以x升序
// 小于0,a在b前面
// 大于0,b在a前面
// 等于0,不变
arr.sort((a, b) => {
return a.x - b.x
})
return divide(arr)
}
function divide(arr, left=0, right=arr.length-1) {
// 如果left=right就返回一个最大值
if(right - left < 1) return Number.MAX_VALUE
if(right - left === 1) {
return getDistance(arr[left], arr[right])
}
// 这里应该向上取整,因为left和right是下标,当left+right是奇数时,其实真正的个数是偶数个
let middle = Math.ceil((left + right) / 2)
let leftMin = divide(arr, left, middle)
let rightMin = divide(arr, middle + 1, right)
let min = Math.min(leftMin, rightMin)
// 中间应该是以middle往两边各占min的距离,在这块区域内通过这些点拿到最短的距离
// i左j右
for(let i = middle; i >= 0; i--) {
for(let j = middle; j <= right; j++) {
if(arr[j].x - arr[i].x <= min * 2) break
let middleMin = getDistance(arr[j], arr[i])
min = Math.min(min, middleMin)
}
}
return min
}
function getDistance(num1, num2) {
return Math.sqrt((num1.x - num2.x) ** 2 + (num1.y - num2.y) ** 2)
}
(9)循环赛日程表
(10)汉诺塔
③分治算法的思维过程:通过数学归纳法,求得方程式,然后设计递归
a、找到最小规模的方程
b、考虑规模增大时的方程
c、找到递归方法
2)动态规划算法
跟分治算法有点相同,也是把一个问题划分为多个小问题,但是会丢弃某些非最优解,直到无法转换,最后的那个最优解就是结果
状态方程就是把所有状态弄出来,然后择优
①动态规划适合的情况
a、最优解的子问题的解也是最优的
b、某阶段状态只与当前状态有关,与后面分出的子问题无关
c、有重叠子问题,该阶段的状态在下一阶段也会用到(这是动态规划比其他算法高效的地方)
②关于动态规划的经典问题
a、斐波拉契数列
步骤一:暴力的递归算法
function fib(n) {
if(n <= 2) return 1;
return fib(n - 1) + fib(n - 2);
}
设N = 20
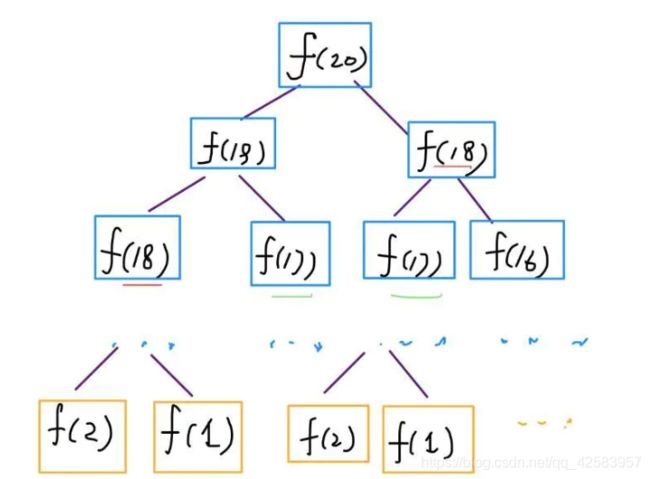
这个递归树的理解就是,要得到 f(20),就要得到 f(19) 和 f(18),直到 f(1) 和 f(2) 是已知的,就不再递归了
递归算法的时间复杂度是子问题的个数,即O(2^N)
根据时间复杂度各级别排序:O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
从中可以看出递归的速度其实没那么好,除此之外,可以从图中发现有很多重复的子问题,而分治算法中有说到要尽量避免重复子问题,所以这里不用分治,而动态规划就是要有重复子问题的算法
步骤二:带备忘录的递归算法
从步骤一可以看出,其实最耗时的就是重复的子问题,所以可以通过备忘录来解决,分解成子问题后马上去查找备忘录,如果里面有就直接取,没有再计算,备忘录一般都是一维数组,当然用字典等都可以
var arr = []
function fib(n) {
if(n <= 2) return 1;
if(arr[n - 1]) {
return arr[n - 1]
} else {
arr[n - 1] = fib(n - 1) + fib(n - 2)
return arr[n - 1]
}
}
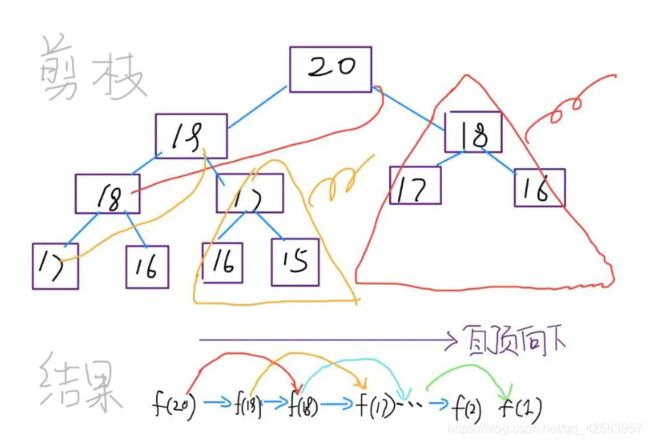
这样就极大的减少了子问题的个数,时间复杂度降为O(N)
从时间复杂度来看,带备忘录的递归算法和动态规划的时间复杂度是一样的,都是O(N)
但是,动态规划是自底向上,而这里是自顶向下
步骤三:自底向上的非递归算法
这个就相当于使用的斐波拉契数列的数学意义,前两个相加等于后面的哪一个,而 fib(n) = fib(n - 1) + fib(n - 2) 以及 fib(1) = fib(2) = 1 就是动态规划中的状态转移方程
function fib(n) {
let arr = [0, 1, 1]; // 把第一个数空出来
for(let i = 3; i <= n; i++) {
arr[i] = arr[i - 1] + arr[i - 2];
}
return arr[n]
}
为什么叫做动态转移方程?
fib(n) = fib(n - 1) + fib(n - 2),从状态 n 变为了状态 n - 1 和状态 n - 2 而已
动态转移方程都是暴力解开,找规律得到的,而这个动态转移方程是动态规划里最重要的东西
另外,这个斐波拉契数列的程序其实还可以简便,因为后一个数只是与前两个数有关,所以可以把空间复杂度降到O(1)
function fib(n) {
let pre = 1;
let after = 1;
for(let i = 3; i <= n; i++) {
let temp = after;
after = pre + after;
pre = temp;
}
return after;
}
斐波拉契函数其实严格意义上来讲不是动态规划算法,因为没有涉及最优解,一旦使用max、min、循环、求最优解等,十有八九都是动态规划
b、凑零钱问题 leetcode322
题目:给你 k 种面值的硬币,面值分别为 c1, c2 … ck,再给一个总金额 n,问你最少需要几枚硬币凑出这个金额,如果不可能凑出,则回答 -1
比如说,k = 3,面值分别为 1,2,5,总金额 n = 11,那么最少需要 3 枚硬币,即 11 = 5 + 5 + 1 。下面走流程。
首先说一下,这里为什么动态规划好:
不仅是因为求最优解,而且每个子问题不会影响父问题,毕竟硬币的个数是无限的,不是说子问题中用了一个,父问题就要少一个,举个例子,就是说你考语文100,和考数学100是没有关系的,但如果你的两个子问题此消彼长,无法同时达到最优解,就没办法用动态规划算法
步骤一:递归暴力解法
根据那个例子,凑11的零钱,其实就可以想象成,我们把每次的钱都分为各个面值1、2、5的,然后再在剩下的零钱中再分,直到最后结果为0,然后我们比较哪个分的次数少(其实就是层数越少越好)就可以了,如图所示
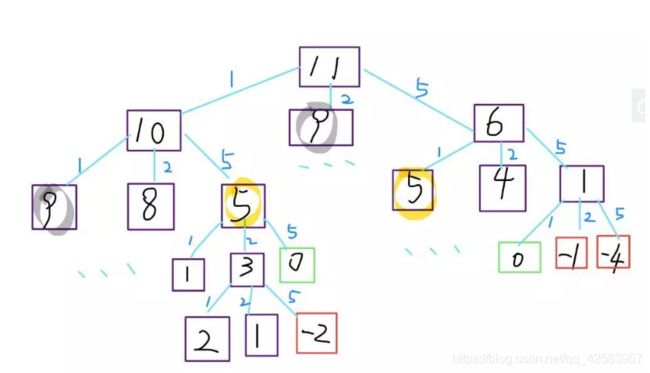
所以写出状态转移方程
这个状态方程的解答是:用一个硬币(价格未知)+价值为XX的硬币集
以上面那个例子来说就是 一个1(价格为 ci)元硬币 + 最小个数的10元(价格为 n - ci)硬币,如果是面值为2,3,则是一个2元硬币 + 最小个数的9元硬币,下面公式的1代表的是一个硬币,而非硬币面值
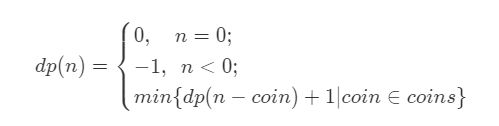
// k为一个数组,里面放的是各种面值
function coin(account, k) {
// 如果金额小于0,返回-1
if(account < 0) {
return -1
}
// 如果金额为0,则不需要硬币(但是要返回0,因为万一是之前算的,就要+1)
if(account == 0) return 0
// 因为是求最小,先把结果定为最大
let res = Number.MAX_VALUE;
// 其实就是一枚硬币+剩下的面额,因为不知道这一枚硬币面值多少,所以用循环
for(let value of k) {
// 通过递归获得剩余钱的次数
temp = coin(account - value, k);
// 如果发现次数为-1,则去下个循环
if(temp == -1) continue;
// 求最小
res = Math.min(res, temp + 1)
}
return res = res !== Number.MAX_VALUE ? res : -1
}
这个的时间复杂度是O(k * n^k),其中总共有 n^k 个节点,且内部要有循环,所以是 k * n^k
步骤二:带备忘录的递归算法
子问题同样有很多重复的,所以可以简便写成:
let money = {}
// k为一个数组,里面放的是各种面值
function coin(account, k) {
// 结束条件
if(account == 0) return 0;
if(account < 0) return -1;
let res = Number.MAX_VALUE;
for(let value of k) {
let temp = 0;
let other = account - value;
if(money[other.toString()]) {
temp = money[other.toString()]
} else {
// 递归
temp = coin(other,k)
money[other.toString()] = temp;
}
// 循环条件
if(temp == -1) continue;
res = Math.min(res, temp + 1)
}
return res !== Number.MAX_VALUE ? res : -1;
}
所以就少了很多重复的,时间复杂度变为O(k*n),毕竟循环去不掉
c、自底向上的非递归算法
因为最低的面额都是1元,所以可以得到的 dp 数组的个数应当有 account 个(这是在最多硬币次数的情况下),但是因为下标为0需要占位(这样也方便加),所以得到下表

/**
* @param {number[]} coins
* @param {number} amount
* @return {number}
*/
var coinChange = function(coins, amount) {
let dp = new Array(amount + 1).fill(Infinity)
dp[0] = 0
for(let i = 1; i < dp.length; i++) {
for(let coin of coins) {
if(coin <= i) {
dp[i] = Math.min(dp[i], dp[i - coin] + 1)
}
}
}
return dp[amount] === Infinity ? -1 : dp[amount]
};
/**
* @param {number[]} days
* @param {number[]} costs
* @return {number}
*/
var mincostTickets = function(days, costs) {
if(days.length === 0) {
return 0
}
let last = days[days.length - 1]
let dp = new Array(last + 1).fill(Infinity)
dp[0] = 0
// 其实在开始时买票和结束时买票最后都要买票,为了方便这里想成结束时买票
let count = 0
for(let i = 1; i < dp.length; i++) {
// 假设只有到了那一天才能买票
if(days[count] === i) {
// 可以是7天前买的票,也可以是今天
let sevenDay = i - 7 >= 0 ? i - 7 : 0
// 可以是30天前买的票,也可以是今天
let thrityDay = i - 30 >= 0 ? i - 30 : 0
dp[i] = Math.min(dp[i - 1] + costs[0], dp[i])
dp[i] = Math.min(dp[sevenDay] + costs[1], dp[i])
dp[i] = Math.min(dp[thrityDay] + costs[2], dp[i])
count++
} else {
dp[i] = dp[i - 1]
}
}
return dp[last]
};
c、动态规划解决博弈问题(以双人拿石子为例)
假设有很多堆石子,两人去取这些石子,每人一次只能取一堆,求最后两人最大的石子差
假设石子为 piles = [3, 9, 1, 2]
首先这里的dp应该用二维数组,dp[i][j]就表示从第i堆的石子到第j堆的石子,除此之外dp[i][j]里面可以存个对象放先手(pre)和后手(after)总共得到的石子数
dp[i][j].pre = max(拿左边 + dp[i + 1][j].after,拿右边 + dp[i][j - 1].after)
为啥是这样的呢,因为如果这一步是先手,那么下一步必定是后手,只不过是拿哪一个地方的后手而已,还有就是为什么先手要考虑下一步呢?因为如果先手有主动权,那肯定是要拿能让下一步和这一步都最大化的那一手,如果只拿这一步最大的,可能下一步被后手追上
而如果先手拿了左边,后手只能拿i + 1 到 j 的先手,如果先手拿了右边的先手,后手只能拿 i 到 j - 1 的先手
相当于先手左边:dp[i][j].after = dp[i + 1][j].pre
先手右边:dp[i][j].after = dp[i][j - 1].pre
如果i = j,那么 dp[i][j].pre = piles[i],dp[i][j].after = 0,毕竟就一堆,先手拿了,后手就没了
得到图
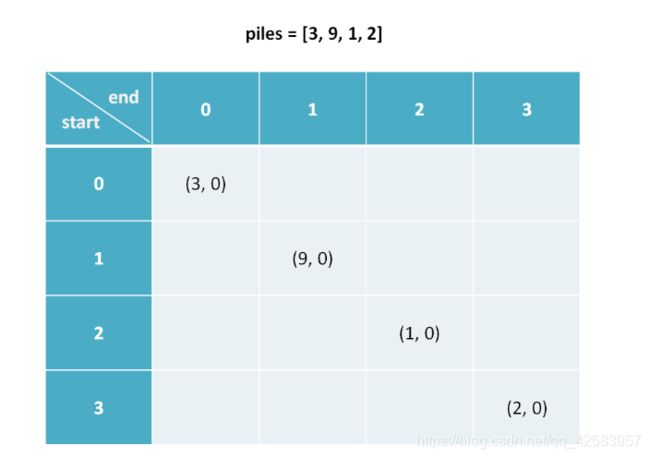
因为 dp[i][j] 的值与 dp[i + 1][j] 和 dp[i][j - 1] 有关,所以就要用备忘录存起来
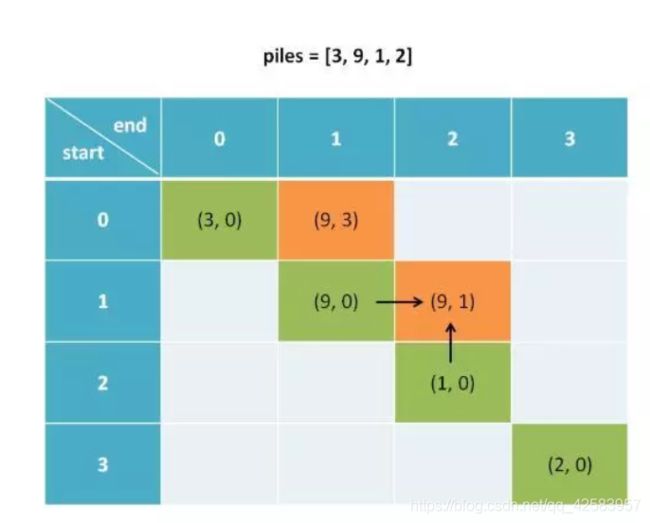
最后结果是:通过 dp[0][3].pre - dp[0][3] 能够得到最大差值
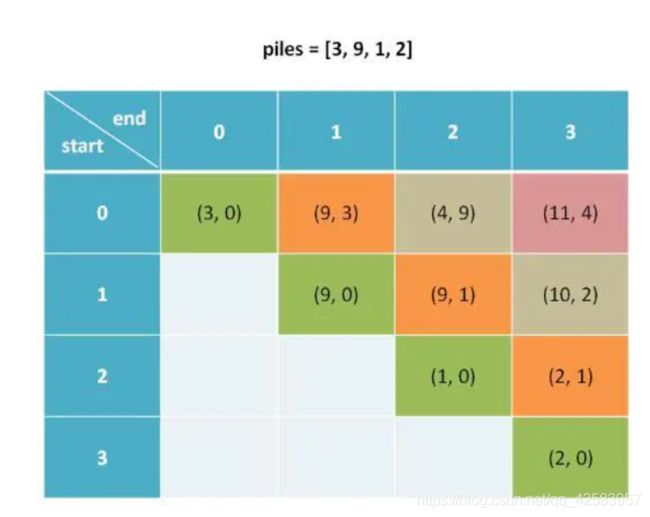
function pile(piles) {
let length = piles.length;
// 先拿到二维数组,让他们初始化先手后手都为0,不要用fill创建带引用对象的东西,因为是浅克隆
let res = new Array(length)
// 把斜对角上的先赋值
for(let i = 0; i < length; i++) {
res[i] = new Array(length)
for(let j = 0; j < length; j++) {
if(i === j) {
res[i][i] = {pre: piles[i], after: 0};
} else {
res[i][j] = {pre: 0, after: 0};
}
}
}
// 这里有个特点,就是要斜着遍历,从(0,1)->(1,2)->(2,3)->(0,2)等
// 从这里可以看出每次第一个都是0开始,所以内层循环i从0开始,终止条件用k来控制一下
for(let k = 1; k <= length - 1; k++) {
for(let i = 0; i < length - k; i++) {
// 找的j纯粹靠暴力看
let j = i + k;
if(i === j) continue;
let left = piles[i] + res[i + 1][j].after
let right = piles[j] + res[i][j - 1].after
// 如果左边大
if(left > right) {
res[i][j].pre = left;
res[i][j].after = res[i + 1][j].pre
} else {
res[i][j].pre = right;
res[i][j].after = res[i][j - 1].pre
}
}
}
return res[0][length - 1].pre - res[0][length - 1].after;
}
d、0-1背包问题
有N件物品和一个容量为V的背包,每件物品都有自己的重量,且只有一件,只能选择放或不放,求能放进背包的物品最大价值
思路:这道题其实类似于之前说的凑硬币,不过因为这道题有两个状态会变化(价值和重量,有点像博弈里的先手和后手各自的堆数不同),所以是二维数组(代表在这几件物品的最高价值,如果创成一维数组,就不知道之前是否使用了某个背包),长度为N*V

// value是背包价值,weight是背包重量
function bug(value, weight, bugWeight) {
// dp[i][j] = x 表示前i个物品共重量j,最大价值为x
// 因为是两个状态(价值和重量),所以二维数组
// dp[0][...] 和 dp[...][0] 没啥用,主要是为了方便
let dp = new Array(weight.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(bugWeight + 1).fill(0)
}
for(let i = 1; i < dp.length; i++) {
for(let j = 1; j < bugWeight + 1; j++) {
// 如果当前物品重量超过设置的状态二的总重量,那么就不放
if(j < weight[i - 1]) {
dp[i][j] = dp[i-1][j]
continue
}
// 选择为当前物品是否要放,放就是dp[i-1][j-weight[i-1]]+weight[i-1]
// 不放就是dp[i-1][j]
dp[i][j] = Math.max(dp[i-1][j-weight[i-1]] + value[i-1], dp[i-1][j])
}
}
return dp[weight.length][bugWeight]
}
e、子集背包问题
子集背包问题其实就是分割俩子集,求和把它转换为背包问题
可以先把这个非空数组求和,然后看分割成两个子集的N个值,是否能装进容量为 SUM/2 的背包
所以这道题的状态是第几个数,这个数的值,对应背包问题的第几个物品,这个物品的重量
然后选择就是是否要选进去

function isMiddle(arr) {
let sum = arr.reduce((a, b) => a + b)
// 如何和为奇数,就不可能返回两个相等和的数组
if(sum % 2 !== 0) return false
sum /= 2
// dp[i][j] = false 表示前i个总和不为j,true就是为j
let dp = new Array(arr.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(sum + 1).fill(false)
// 如何和为0,那肯定是满了的,就是true(这一步很重要,否则之后就无法给dp赋值true)
dp[i][0] = true
}
for(let j = 1; j < sum + 1; j++) {
for(let i = 1; i < arr.length + 1; i++) {
if(arr[i - 1] > j) {
dp[i][j] = dp[i - 1][j]
continue
}
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - arr[i]]
}
}
return dp[arr.length][sum]
}
然后又因为其实这个里面没必要划分物品(毕竟物品自身没有属性),所以可以用一维数组表示dp
function isMiddle(arr) {
let sum = arr.reduce((a, b) => a + b)
// 如何和为奇数,就不可能返回两个相等和的数组
if(sum % 2 !== 0) return false
sum /= 2
// dp[i][j] = false 表示前i个总和不为j,true就是为j
let dp = new Array(arr.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(sum + 1).fill(false)
// 如何和为0,那肯定是满了的,就是true(这一步很重要,否则之后就无法给dp赋值true)
dp[i][0] = true
}
for(let i = 1; i < arr.length + 1; i++) {
for(let j = 1; j < sum + 1; j++) {
if(arr[i - 1] > j) {
dp[i][j] = dp[i - 1][j]
continue
}
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - arr[i]]
}
}
return dp[arr.length][sum]
}
f、完全背包问题
将N个物品各自有重量,放进一个重量为M的背包中,物品数量无限可重复,问有多少种放法就是完全背包问题
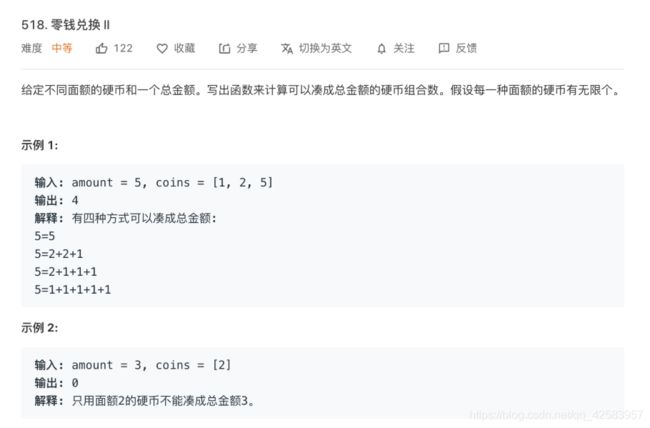
这里for循环的位置特别重要,因为是要将所有选择都加在一起才算到总共耗费方法的
function getCount(arr, amount) {
// dp[i] = x 表示当总共有i元有x种凑齐方法
let dp = new Array(amount + 1).fill(0)
// 当0元肯定有1种凑齐方法
dp[0] = 1
// 必须先循环钱的面额,再循环每一笔钱
// 因为我们是将选择这个硬币和不选这个硬币加在一起才得到该费用的几种方法
for(let value of arr) {
for(let i = 1; i < amount + 1; i++) {
if(i < value) {
dp[i] = dp[i - 1]
continue
}
dp[i] = dp[i] + dp[i - value]
}
}
return dp[amount]
}
g、编辑距离问题(其实就类似diff,但是vue2没有使用动态规划)

具体步骤见 经典动态规划指南
// 认为应该让str1变成str2
function getCounts(str1, str2) {
// dp[i][j] = x 表示0-i下标的arr1和0-j下标的arr2,需要操作x次
let dp = new Array(str1.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(str2.length + 1).fill(Number.MAX_VALUE)
}
// base case,把dp[0][...] 和 dp[...][0] 设置一下
for(let i = 0; i < dp.length; i++) {
dp[i][0] = i
}
for(let i = 1; i <= str2.length; i++) {
dp[0][i] = i
}
for(let i = 1; i <= str1.length; i++) {
for(let j = 1; j <= str2.length; j++) {
// 如果相等,操作数就用之前的
if(str1[i - 1] === str2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1]
continue
}
// 这里有三种选择,增、删、替换,找到操作数使用最小的一种即可
// 增
// (在str1的i指针指向的后面插入一个字母,所以下次要把j指针往前移动,与i比较)
// dp[i][j] = dp[i][j - 1] + 1
// 删
// (把str1的i指针所指的删掉,这个时候i指向之前那个i指向的后一个的数,所以要把i往前移动)
// dp[i][j] = dp[i - 1][j] + 1
// 替换
// (换完之后两边指针都要往前移动)
// dp[i][j] = dp[i - 1][j - 1] + 1
dp[i][j] = min(dp[i][j - 1] + 1, dp[i - 1][j] + 1, dp[i - 1][j - 1] + 1)
}
}
return dp[str1.length][str2.length]
}
function min(a, b, c) {
return Math.min(a, Math.min(b, c))
}
h、高楼扔鸡蛋
总共有1-N的N层楼,有k个鸡蛋,问最坏情况下,至少扔多少次知道鸡蛋恰好不碎
读题干,有两个词很重要,最坏和至少
先考虑最少那就可以使用二分查找法,而非线性查找法,毕竟线性查找是一层一层找的
最坏我们可以理解为是第i层楼碎不碎是看二分查找中 [0, i -1] 和 [i + 1, n] 哪儿个找的多
所以根据题干就可一直到我们 dp[i][j] = min(max())
// n是楼层数,k是鸡蛋数
function egg(n, k) {
// 这里有两个状态,鸡蛋数和楼层数,所以dp是二维数组
// dp[i][j] = x 表示如果搜索共i层恰好不碎,在最坏情况下,花j个鸡蛋最少扔x次确定
// 总共0层和没有鸡蛋时肯定不用扔都能确定
let dp = new Array(n + 1)
for(let i = 0; i < n + 1; i++) {
dp[i] = new Array(k + 1).fill(0)
}
// basecase:
// ①如果是0层或者0个鸡蛋一定只要0次(这个在上一步做了)
// ②如果是n层,m个鸡蛋,n>=m时最大次数为m,n= j) {
dp[i][j] = j
} else {
dp[i][j] = i
}
}
}
for(let i = 2; i < n + 1; i++) {
for(let j = 1; j < k + 1; j++) {
// 如果在搜索i层碎了,那么就应该搜索[1,i-1]层楼,共i-1层楼
// 此时的鸡蛋数目也少了一个,为j-1,所以此时搜索次数是dp[i-1][j-1] + 1
// 而如果在搜索i层时没有碎,那么就应该搜索[i+1,n],共n-i层楼
// 此时鸡蛋数目不少,毕竟没碎,还是j,所以此时搜索次数为dp[n-i][j] + 1
// 然后这两个中要求出最大的,毕竟是最坏情况
dp[i][j] = Math.min(dp[i][j], 1 + Math.max(dp[i - 1][j - 1], dp[n - i][j]))
}
}
return dp[n][k]
}
I、戳气球问题

这道题虽然用回溯会很简单,但是,如果有500个气球,就相当于全排列500!,时间复杂度和空间复杂度都很坏(具体过程见下面回溯)
所以这里考虑用动态规划
其中,dp使用二维数组,毕竟是找范围内的解(虽然这里直接看状态,不一定能看出二维数组这个),dp[i][j]代表在i+1到j-1范围内的最大硬币数量,为什么这里不包含i和j这两个气球呢,这里可以看下图
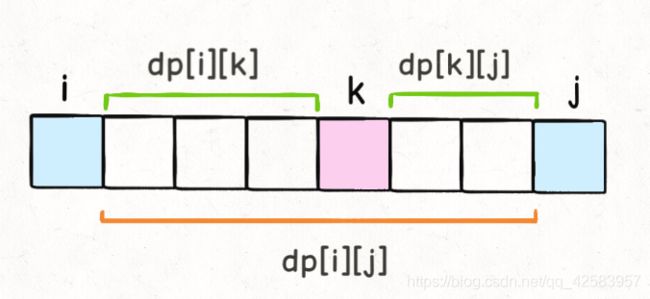
假设在i和j中,最后被戳破的是nums[k],那么dp[i][k] 和 dp[k][j] 就是之前戳破了的,对于戳破第k个气球的得分就应当是 dp[i]*dp[k]*dp[j] + dp[i][k] + dp[k][j]
然后我们来考虑下 base case,如果 i = j,那么得分一定是 0,然后我们画出二维数组图
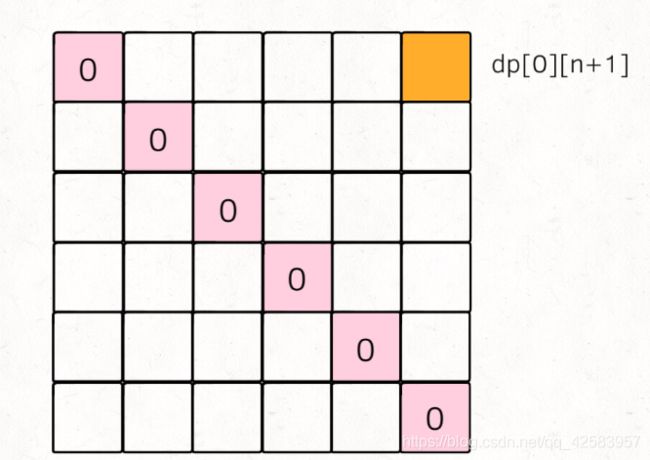
然后我们根据状态方程:dp[i][j] = Math.max(dp[i][j], nums[i] * nums[k] * nums[j] + dp[i][k] + dp[k][j]
所以我们要想得到 dp[i][j] 就必须得到 dp[i][k] 和 dp[k][j],如图
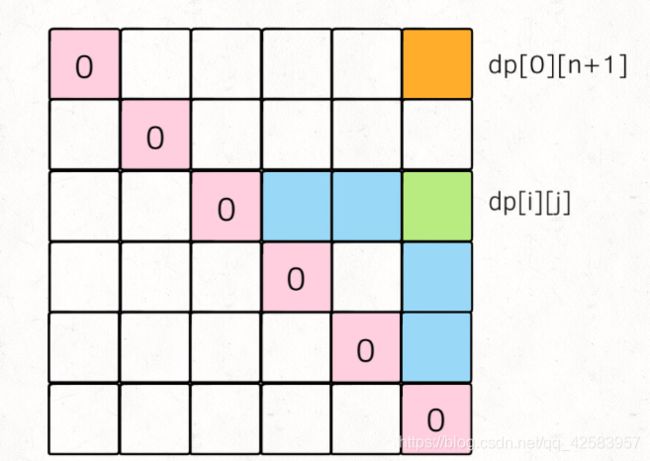
要得到蓝色部分,我们很自然的就能想到斜着遍历,所以具体的代码如下
function balloon(arr) {
// 因为定义的dp是开区间,所以arr要在两边加一个1
arr = [1, ...arr, 1]
// dp[i][j]指的是从第i+1到第j-1个气球的乘积和,i<=j, base case是0
let dp = new Array(arr.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(dp.length).fill(0)
}
// 斜着遍历
for(let k = 1; k < dp.length; k++) {
for(let i = 0; i < dp.length - k; i++) {
let j = i + k - 1
// dp[i][j] 其实就是比较自己和dp[i][k]+dp[k][j]+arr[i]*arr[k]*arr[j]
for(let k = i + 1; k < j; k++) {
dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k][j] + arr[i] * arr[k] * arr[j])
}
}
}
// 毕竟开区间返回的就是从第一个到现在arr的倒数第二个,以前arr的最后一个
return dp[0][arr.length - 1]
}
j、最长公共子序列
这道题跟下面讲解动态规划思维中提到的递增子序列差不多,都是子序列问题
这里再重复一遍,子序列不需要紧邻,但是子串需要紧邻,一般求子序列问题多半是动态规划,像这样对字符串进行复杂操作的一般都是动态规划,而且一般dp都是二维数组,如之前的g编辑距离,求两个字符串最少的增删改次数

function getLength(str1, str2) {
// dp[i][j]表示对str1从第1个到第i个与str2从第1个到第j个的最大公共子序列个数
let dp = new Array(str1.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(str2.length + 1).fill(0)
}
for(let i = 1; i < dp.length; i++) {
for(let j = 1; j < str2.length + 1; j++) {
if(str1[i - 1] !== str2[j - 1]) {
// 看是[1, i-1]的子序列个数大,还是[1, j-1]的子序列个数大
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1])
} else {
dp[i][j] = dp[i - 1][j - 1] + 1
}
}
}
return dp[str1.length][str2.length]
}
k、四键键盘

首先思考dp,这里使用一维数组,也就是说dp[i]表示第i个键盘最多的A的数量
然后考虑选择,总共就两个选择
当敲键盘数量很少时,全部都敲A是最大的,也就是dp[i] = dp[i - 1] + 1,毕竟dp[i - 1] 表示有 i - 1 次敲键盘机会中最多的A的数量
第二种就是 A A A ……ctrlA ctrlC ctrlV 然后ctrlA,ctrlC,ctrlV这样循环,或者直接全ctrlV,但无论如何,永远都以ctrlV来结尾(在这道题代码中,干脆就直接全使用ctrlV,不要其他的了),所以其实直接可以用一个for循环来找第一个ctrlV,后面的个数也能得到了
function getCount(num) {
let dp = new Array(num + 1).fill(0)
dp[1] = 1
for(let i = 2; i < dp.length; i++) {
// 在之前最优的情况下按A键
dp[i] = dp[i - 1] + 1
// j是ctrl+v开始的地方,因为ctrl+v前面必定至少有A,ctrl+a,ctrl+v,所以应当从3开始
// 毕竟初始化的时候用的是 num + 1
for(let j = 3; j < i; j++) {
// 比较前一个按A和前俩是ctrl+a和ctrl+c
// dp[j - 2]是去掉ctrl+a和ctrl+c后共有的最多的A数量
// 总共会用i-j个ctrl+v
dp[i] = Math.max(dp[i], dp[j - 2] * (i - j + 1))
}
}
return dp[num]
}
L、KMP字符串匹配算法
这个算法其实就是题目给一个str,一个pattern,匹配pattern在str中的位置
如果是暴力解法,就是双层循环,如果pattern的某一位找不到,就把str的指针又倒回原处然后往下移一个,然后继续循环
而KMP就是让str的指针不会后退,但是pattern的指针会进行最小的后退数目
function KMP(str, pattern) {
// 如果要匹配的字符串个数太少,那就说明铁定匹配不到
if(str.length < pattern.length) return -1
// 新建的dp只跟pattern有关
// dp[i][j] = n 表示当前状态(这里的状态都是指匹配到pattern的第几个字符)如果碰到字符j,下一步会跳到状态n
// 所以dp[i][j] = n 可表示为 dp[1]['A'] = 2
// 意思是当现在已经匹配一个字符后,下一步如果要匹配'A',那么会将pattern的下标移到2,2代表现在前缀和后缀相等的最大字符数
// 另外,i的状态是pattern已匹配的个数,j指的是str中目前指向的地方
// 前缀针对的是现在匹配了的pattern部分,也就是说当现在 pattern = 'ABABC'
// 前缀有'A'、'AB'、'ABA'、'ABAB'
// 后缀有'C'、'BC'、'ABC'、'BABC'
// 这里没有重复的,所以要跳转的状态是0
let dp = new Array(pattern.length)
for(let i = 0; i < dp.length; i++) {
// 这里使用str.length是因为最多就str.length个字母
dp[i] = {}
}
let buildKmp = function() {
// base case,从第0步用第一个字符匹配,下一步应该跳到1
// 如果在初始位置用除了第一个字符以外的字符匹配,会仍然留在原地
dp[0][str[0]] = 1
// x是和j有相同前缀的位置
let x = 0
for(let i = 0; i < dp.length; i++) {
for(let j = 0; j < str.length; j++) {
// 因为dp[i]里面可能并没有设置键为str[j]的
// 所以在这里初始化
// 用Object.prototype.hasOwnProperty查看是否有这个键
// 没有就初始化成0
// 因为dp[i]为{}
// 如果直接用{}.hasOwnProperty(),{}不会被认为是对象
// 而是代码块,所以要用括号,表明这是对象
// 但是直接用dp[i]算出了是{}然后用.xxx是不会报错的
if(!dp[i].hasOwnProperty(str[j])) {
dp[i][str[j]] = 0
}
// 如果dp[x][str[j]]没有,那么也要初始化
if(!dp[x].hasOwnProperty(str[j])) {
dp[x][str[j]] = 0
}
// 如果能够匹配到该字符,就往前走(即j+1)
if(str[j] === pattern[i]) {
dp[i][str[j]] = i + 1
} else {
// 否则就退回到之前记录的有相同前缀的位置
// 这里不直接用x是因为回退其实也分情况
// 如果直接用x就固定成一种情况了,而且不清楚这是否正确
// 但是用dp[x][str[j]]就会直接指向正确的一种情况
dp[i][str[j]] = dp[x][str[j]]
}
}
// 更新x,x为目前能得到的下一步状态
x = dp[x][pattern[i]]
}
}
let search = function() {
// 当前状态(pattern指向的位置)
let i = 0
// j 表示str字符指针末尾的位置
for(let j = 0; j < str.length; j++) {
// 下一状态
i = dp[i][str[j]]
// 如果下一状态到达了pattern末尾就说明已经找到结果了
if(i === pattern.length) {
// 返回的是下标
return j - i
}
}
return -1
}
buildKmp()
let res = search()
return res
}
M、股票买卖问题
①只允许买卖一次股票的情况:

②买卖两次股票

买卖一次和买卖两次或买卖n次(0 < n <= arr.length/2)都可以用以下模板
// k为最多买卖次数(买一次+卖一次=1次买卖次数)
function money(arr, k=Number.MAX_VALUE) {
// 如果可买卖次数比总天数都多,那么就相当于无限次
if(k * 2 > arr.length) {
money_infinity(arr)
}
// 传入次数且买和卖的次数和不超过数组的个数时,我们创建一个三维数组
// 用来处理次数
// dp[i][j][m] = n
// 表示在第i天共能做j次操作此时在持有股票或不持有股票的状态下利润为n
// 其中,m为0表示不持有股票,m为1表示持有股票
let dp = new Array(arr.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(k + 1)
for(let j = 0; j < k + 1; j++) {
dp[i][j] = new Array(2).fill(0)
}
}
// base case
// 因为我把持有和未持有股票是分开了的
// 所以我们可以直接手写产生的情况
// 假设第一天就买了,一定是-arr[0],但是如果我们使用dp,他就一定会选择不买
// 所以这里我们只能手写
for (let i = 1; i <= k; i++) {
dp[1][i][1] = -arr[0]
}
// 这里可以只要两层循环,毕竟最里面的那一层只有0和1
// 而且因为持有和未持有股票会对操作带来影响,所以直接暴力手写
// 从第二天开始是因为,我们自己把第一天的base case写出来了
// 买的话是-arr[0],而因为是第一天,所以不可能卖
for(let i = 2; i < dp.length; i++) {
for(let j = k; j > 0; j--) {
// 不持有股票情况下,应该有两种情况
// 之前一天持有股票但是卖了,dp[i-1][j-1][1] + arr[i - 1]
// 关于为什么要加上arr[i - 1],因为如果在这一天卖出,卖出这天的钱就能变成利润
// 关于为什么是之前一天,我们求的dp是最大利润
// 为什么是j-1,毕竟使用了一次买入或卖出就相当于用过了一次操作
// 也就是说哪怕之前连续持有股票很多天,前一天的利润一定是最大的
// 或者是之前就没有股票,保持原状,dp[i-1][j][0]
dp[i][j][0] = Math.max(dp[i - 1][j][1] + arr[i - 1], dp[i-1][j][0])
// 如果是持有股票的情况下,也有两种情况
// 之前没股票,然后买了,dp[i - 1][j][0] - arr[i - 1]
// 买入肯定要从利润里扣钱
// 如果是保持原样就是,dp[i - 1][j][1]
dp[i][j][1] = Math.max(dp[i - 1][j - 1][0] - arr[i - 1], dp[i - 1][j][1])
}
}
// 最后结果一定是卖出,毕竟卖出的钱最多(至少能捞一笔回来)
return dp[arr.length][k][0]
}
③买卖次数无限
对于买卖n次(n > arr.length/2)或可以买卖无限次的,使用以下模板
function money_infinity(arr) {
// 这里应该创建一个二维数组,毕竟如果可以买卖多次
// 就相当于不需要对次数做限制
// 管他买卖多少次,只要最后利润最高即可
// dp[i][j] = n 表示第i天如果在j情况(j=0不持有股票,j=1持有股票)
// 最大的利润为n
let dp = new Array(arr.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(2).fill(0)
}
// base case
// 第一天如果就有,那就说明买了
dp[1][1] = -arr[0]
// 从第二天开始,毕竟第一天的我们可以手推
for(let i = 2; i < dp.length; i++) {
// 若不持有股票
// 则可能为原先就没有dp[i-1][0]
// 或者前一天有,卖了,dp[i-1][1]+arr[i-1]
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]+arr[i-1])
// 若持有
// 则可能原先就有,dp[i-1][1]
// 前一天没有,今天买了,dp[i-1][0]-arr[i-1]
dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]-arr[i-1])
}
return dp[arr.length][0]
}
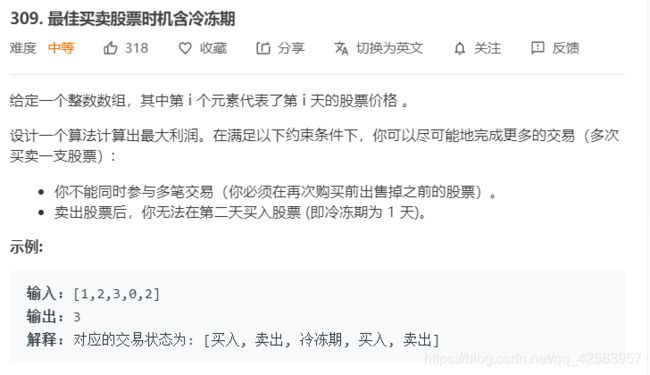
// 如果有冷冻期
function money_infinity_cold(arr) {
let dp = new Array(arr.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(2).fill(0)
}
dp[1][1] = -arr[0]
for(let i = 2; i < dp.length; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + arr[i - 1])
// 如果是要买股票,因为有冷冻期,所以只能按照两天前最高的利润
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][0] - arr[i - 1])
}
return dp[arr.length][0]
}
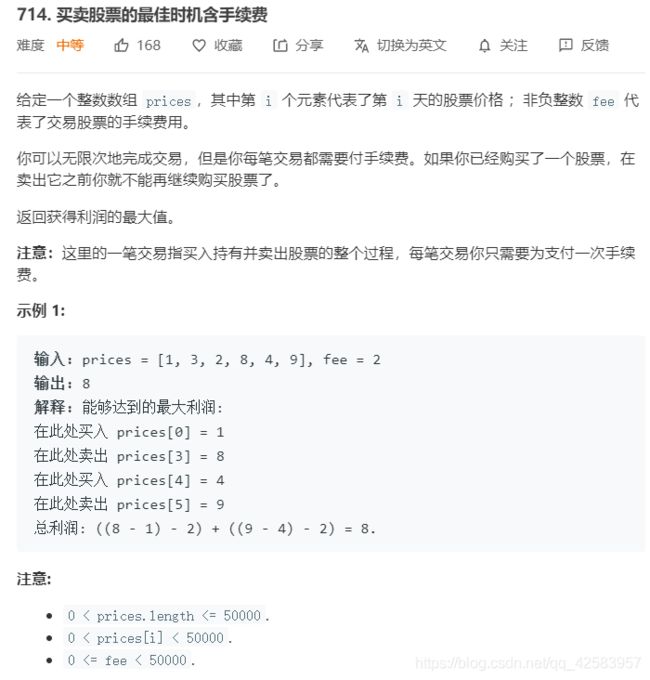
function money_infinity_fee(arr, fee) {
let dp = new Array(arr.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(2).fill(0)
}
dp[1][1] = -arr[0]
for(let i = 2; i < dp.length; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + arr[i - 1] - fee)
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - arr[i - 1])
}
return dp[arr.length][0]
}
N、打家劫舍问题

这个其实有点类似于股票问题中有冻结期的那一种
状态就是总共进了几间房子
function house(arr) {
// dp[i] = x 表示在前i间房屋中最多有x元
let dp = new Array(arr.length + 1).fill(0)
// base case 如果只有一间房子,那就必选这间
dp[1] = arr[0]
for(let i = 2; i < dp.length; i++) {
// 要么选择这第i间房子和倒数第二间房子的总和
// 要么就不选这一间房子,直接为前面那间房子的金额
dp[i] = Math.max(dp[i - 1], arr[i - 1] + dp[i - 2])
}
console.log(dp)
return dp[arr.length]
}
第二种打家劫舍,给的房子是一个圈(首尾相连),也就是说如果给一个数组[3,4,5]那么结果是4,而不是8,因为首尾相连也就是说第一间和第三间都不能同时去偷
可以根据单调栈解决环形数组(具体在其他之中),可以找到解决方法
不过这道题的解决方法其实是考虑到底是否需要首尾(即只要头,只要尾,头尾都不要三种情况)如下

所以我们就相当于依旧是用上面那个方法,不过给的数组不同,仅此而已
function find(arr) {
let getMax = function(arr) {
let dp = new Array(arr.length + 1).fill(0)
dp[1] = arr[0]
for(let i = 2; i < dp.length; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + arr[i - 1])
}
return dp[arr.length]
}
let max = function(a, b, c) {
let temp = Math.max(a, b)
return Math.max(temp, c)
}
// 只有头
let head = getMax(arr.slice(0, arr.length - 1))
// 只有尾
let tail = getMax(arr.slice(1, arr.length))
// 两个都没有
let notTwo = getMax(arr.slice(1, arr.length - 1))
return max(head, tail, notTwo)
}
第三种打家劫舍,假设房子既不是按一排也不是按一圈来排列,而是按照一棵二叉树来排列,相连的就不能偷窃,如图

这道题相当重要,也相当典型!!
O、新21点
这道题主要想说明一个事情:不是所有的动态规划的dp都是求最后一个,也有可能求dp[0],这样倒着来的!

这道题题意其实写得挺让人费解的,这里解析一下,以后遇到这类情景模型题,如何读懂题意:
补充一下21点的知识:主要就是在不使用大小王以外的牌里,用手上的牌来凑和,和不能大于21点,且很大就算赢
根据21点的知识,我们把这道题明确成两种情况,爱丽丝会输和赢,然后又看到题干里说道“爱丽丝的分数不超过N”,也就是这里不是21点,而是N
这道题与普通的21点相比多了一个条件,也就是“当爱丽丝获得不少于K分时,她就停止抽取数字”,这句话的理解是当前和在[K, N]区间时,就算赢(而普通21点是求最大值)
然后我们设置dp[i] = j 表示当现在和为i时,赢的概率是 j
我们很自然地就能知道当K <= i <= N时赢的概率为1,而当N < i < K + W时赢的概率就是0
关于这里为什么开边界是 K + W,因为当你手上的牌的总和等于 K 就无法再抽牌了,在 K - 1 的时候可以抽最后一张牌,面值最大可以抽到 W,这里使用开边界自然就是 K + W,闭边界就是 K + W - 1
所以当dp[0]的时候就是我们要求的结果(代表着从手上没牌,一直摸,赢的几率)
从这里我们就可以看出,我们要倒推出前面的概率
其实如果想求第i个位置的概率,可以用 [i, i + W] 这个范围内的概率 * 1 / w 然后求和,说白了也就是公式
dp[x] = 1/w * (dp[x+1]+dp[x+2]+dp[x+3]...+dp[x+w])
为什么这里使用 1/w 呢,因为这是有放回的抽取,所以总数一直没变,是w(要不然这里使用动态规划也有点麻烦),而且因为有w张卡,随便抽一张概率是 1/w,而对应赢的概率是dp[x+n],和就是抽过所有卡牌尝试的会赢的概率
如图,蓝色部分一部分概率是0,一部分概率是1
需要求的红色部分就是括号所包括的和
橙色部分是还没求到的
![]()

![]()
var new21Game = function(N, K, W) {
let dp = new Array(K + W).fill(0)
let sum = 0
for(let i = K;i <= N; i++) {
dp[i] = 1
sum += 1
}
for(let i = K - 1; i >= 0; i--) {
dp[i] = sum / W
sum += dp[i] - dp[i + W]
}
return dp[0]
};
P、最长回文子串

其实找回文子串天生就很适合动态规划,因为回文子串去掉头尾还是回文子串,然后判断边界就行了
/**
* @param {string} s
* @return {string}
*/
var longestPalindrome = function(s) {
// dp[i][j] = true 表示第i到第j是回文,dp[i][j] = false表示第i到第j不是回文
let dp = new Array(s.length)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(s.length).fill(false)
}
let begin = 0
let maxLen = 1
for(let n = 1; n < dp.length; n++) {
for(let i = 0; i < s.length - n; i++) {
let j = i + n
if(s[i] === s[j]) {
if(j - i < 3) {
dp[i][j] = true
} else {
dp[i][j] = dp[i + 1][j - 1]
}
} else {
dp[i][j] = false
}
if(dp[i][j] && j - i + 1 > maxLen) {
begin = i
maxLen = j - i + 1
}
}
}
return s.substring(begin, begin + maxLen)
};
③动态规划算法的思维过程:递归的暴力解法 -> 带备忘录的递归解法 -> 非递归的动态规划解法
④如何写动态规划算法程序,以求递增子序列的例子说明
首先,自己要写动态规划算法的时候,不能像我们了解原理那样慢慢来,毕竟有时间问题,应该直接去找状态变化方程

子序列不等于子串,子串的顺序必须挨着,子序列可以跳序,但是必须是从左到右
另外,上升序列和非递减序列不一样,因为非递减可以相等,自己是自己最短的上升子序列
这道题的解题思路是,以5为例,我们从左往右找到比他小的,也就是2,也就是比2小的个数 + 1就是5的一个子序列,再找有没有比5小的,然后找出最大的就行了,其实这个跟凑零钱差不多
思路有了,我们就来找dp数组,只要是动态规划来实现的东西,都需要dp数组,不过这些dp数组可能代表的意义不同
这里的dp数组代表最长子序列的个数,一般问什么,dp数组就是什么
然后找找base case(也就是我们从底部能拿到的初始值是什么),本题应该是1,毕竟自己也是自己的子序列
然后写出代码即可
function count(array) {
// 应该初始化为1,毕竟自己就是最小的子序列
let dp = new Array(array.length).fill(1);
for(let i = 1; i < array.length; i++) {
for(let j = 0; j < i; j++) {
if(array[j] < array[i]) {
dp[i] = Math.max(dp[j] + 1,dp[i])
}
}
}
return dp[array.length - 1]
}
我们再来理一理动态规划算法要做啥:
1、判断是否使用动态规划算法
2、找出状态转化方程和状态(一般题目给的参数类型就是状态,一般都能累计或更改)还有选择(是要还是不要,要几个这样)
3、找出dp数组(状态有几个就创建几维数组)
4、找出 base case(dp初始化)
5、写不递归的循环代码
动态规划的伪代码套路
// 伪代码模板
// 一般为了方便,初始化dp一般都是会多初始一个[0],若是二维就是[0][...],[...][0]
let dp = new Array(状态一.length + 1)
// ……如果需要二维也再这样,并初始化
// 假设有个什么价格啊,或者之类传入的就是数组来改变状态的,就要写在状态一前面
// 如 for(let k of arr),这个必须写状态一前面,否则会出错(见完全背包)
for(let a in 状态1) {
for(let b in 状态2) {
……以此类推
// 看下有没有对状态的限制条件
// 有就再看看会被选择成什么
dp[a][b] = 最大或是最小等(选择1,选择2,……)
}
}
return dp[状态一.length][状态二.length][...]
关于dp遍历方向
在 dp[m + 1][n + 1] 情况下,一般 dp[…][0] 和 dp[0][…] 都是base case
①、正向遍历
for(let i = 1; i <= m;i++) {
for(let j = 1;j <= n;j++) {
// 计算dp[i][j]
}
}
②、反向遍历
for(let i = m; i >= 1; i--) {
for(let j = n; j >= 1; j--) {
// 计算dp[i][j]
}
}
③、斜着遍历
for(let k = 1; k < dp.length; k++) {
for(let i = 0; i < dp.length - k; i++) {
let j = i + k - 1
// 计算dp[i][j]
}
}
动态规划的时间复杂度其实就是子问题个数*单个函数的复杂度(不算递归就看for循环)
⑤关于子序列问题的套路模板
如果题目给的是一个字符串求子序列,一般dp都是一维数组,如求递增子序列,以下伪代码
function getCount(str) {
let dp = new Array(str.length + 1).fill(1) // 重点
// base case 的地方
for(let i = 2; i < dp.length; i++) { //重点
for(let j = 1; j < i; j++) { //重点
if(str[j - 1] < str[i - 1]) {
dp[i] = Math.max(dp[i], dp[j] + xxx)
}
}
}
return dp[str.length]
}
如果题目给的是两个字符串求子序列,一般dp是二维数组,如求最大公共子序列或编辑距离
function getCount(str1, str2) {
let dp = new Array(str1.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(str2.length + 1)
}
for(let i = 0; i < str1.length; i++) {
for(let j = 0; j < str2.length; j++) {
if(str1[i] === str2[j]) {
dp[i][j] = dp[i][j] + xxxx
} else {
dp[i][j] = Math.max(dp[i][j], xxxx)
}
}
}
return dp[str1.length][str2.length]
}
举个例子:最长回文子序列

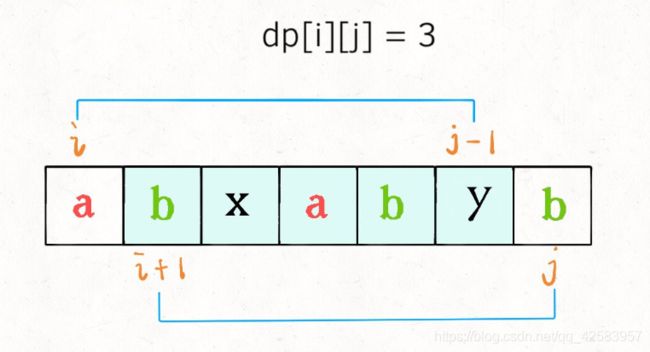
首先,这里的dp设置为二维数组dp[i][j]表示第i位到第j位的最长回文子序列数
然后我们可以根据如下图所述,推出,当 arr[i] === arr[j] 时,dp[i][j] = dp[i + 1][j - 1] + 2
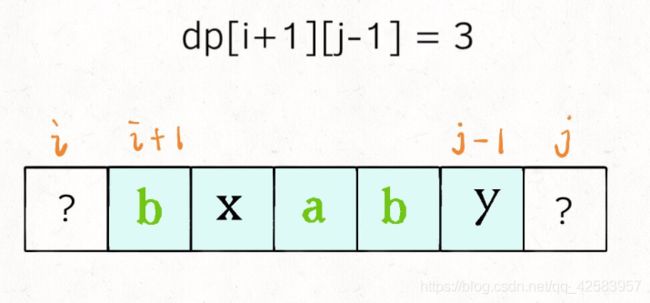

而当 arr[i] !== arr[j] 时,dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]
function getCount(str) {
let dp = new Array(str.length)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(str.length).fill(0)
}
// base case,当i=j时最大为1
for(let i = 0; i < dp.length; i++) {
dp[i][i] = 1
}
for(let k = 2; k <= dp.length; k++){
for(let i = 0; i <= dp.length - k; i++) {
let j = i + k - 1
if(str[i] === str[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1])
}
}
}
return dp[0][str.length - 1]
}
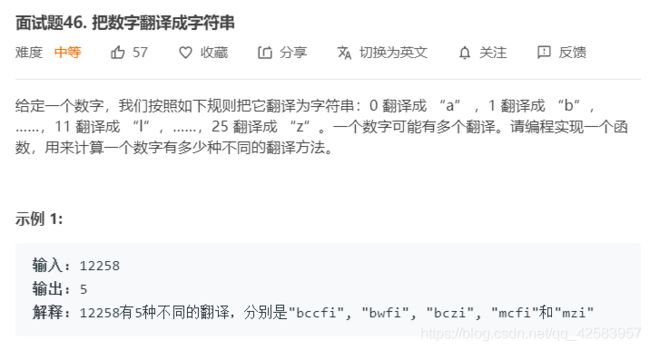
var translateNum = function(num) {
let str = num.toString()
let dp = new Array(str.length + 1).fill(1)
for(let i = 2; i < dp.length; i++) {
let value = parseInt(str[i - 2] + str[i - 1])
if(value < 26 && value >= 10) {
dp[i] = dp[i - 2] + dp[i - 1]
} else {
dp[i] = dp[i - 1]
}
}
return dp[str.length]
};
3)贪心算法
每一步都拿最优的,最后就是最优的,另外01背包问题不能用贪心算法来解决(毕竟贪心无法保证填满)
贪心算法其实是动态规划的一个特例,因为它不像动态规划一样有重复子结构,而动态规划却有
①相关例题
a、区间调度

而下面这一个如果区间相邻气球就会爆炸,如[1,2]和[2,3]只需要一箭

模板:
注意:这里给的代码仅为模板,对应不同的题需要变形
1)先根据end来排序,找到end最小的那个
2)只要其他区间的start超过了end就从原数组中去除
3)如果没有超过(也就是说没有重叠),那么就以这个的end为最新的end,并从原数组中去除,开始下一轮比较
4)直到原数组中没有数据
// 输入实例:[[start,end],[start,end]]
function find(arr) {
let res = []
// 先把区间根据end升序
// sort是原地排序并返回数组
arr.sort((a, b) => {
return a[1] - b[1]
})
// 从原数组中删除,并添加到新数组
res.push([...arr.shift()])
// 定义一个指针,指向新数组中需要检验end那一个
let index = 0
for(let i = 0; i < arr.length; i++) {
// 如果其他区间的start小于第一个放进结果区间的end
// 那么就是重叠的
// 把这个从原数组中去掉
if(arr[i][0] < res[index][1]) {
arr.splice(i, 1)
} else {
// 否则就放进res,并从原数组中删掉
res.push([...arr.shift()])
// 而且如果找到没有重叠的,就以这个的end为新的标准
index++;
}
// 因为去掉之后后面的往前移了一位,所以把下标往前移动
i--
}
return res
}
4)回溯算法
回溯算法其实就是决策树遍历问题,与动态规划一样,回溯也需要思考三个东西:
a、路径:自己曾经做出过的选择
b、选择列表:自己还没做出的选择
c、结束条件:树什么时候到达最底部
①回溯算法的伪代码套路
let res = []
function backtrack(路径, 选择列表) {
if(结束条件) {
res.push(路径)
return
}
for(let 选择 of 选择列表) {
// 这里有时候还要判断下,例如这个选择是不是已经在路径中了
做选择
// 具体操作如下:
// ①将选择放入路径中
// ②将该选择从选择列表中去除
backtrack(路径, 选择列表)
撤销选择
// 具体操作如下:
// ①将路径中的最后一个放入选择列表
// ②将路径中的那个选择去掉
}
}
②相关例子
a、全排列
全排列就是求 n!,假设n = 3,如果我们使用树来表示这个选择过程的话就是
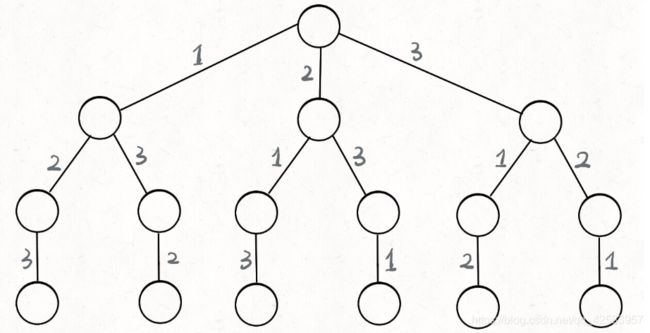
我们还可以精确一点,叫他决策树,毕竟每个节点都在做决定
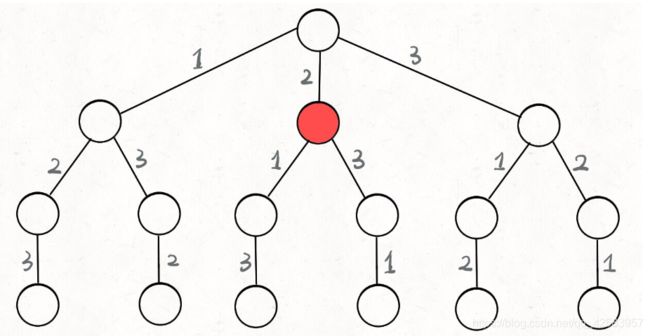
在这个红色的点中,它的路径是[2],选择列表是[1, 3],结束条件就是选择列表为空的时候
下图描述了蓝色节点的属性

然后我们根据回溯伪代码模板,在循环中可以看到三步
做选择
递归
撤销选择
这之中的做选择,其实就是前序遍历,而撤销选择是中序遍历或者后序遍历之一
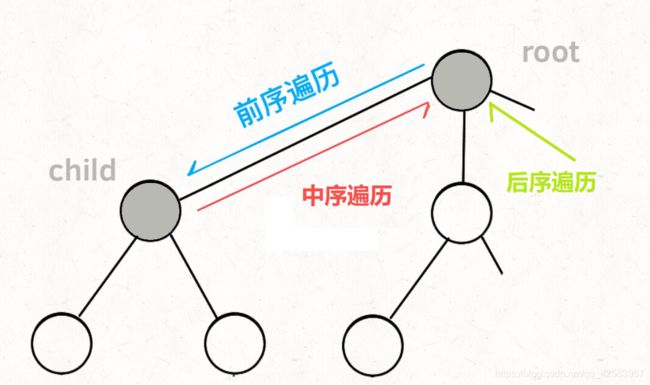

// 输入一组不重复的数字进行排列
function permute(nums) {
let res = []
let path = []
let backtrack = function(nums, path) {
if(path.length === nums.length) {
// 这里不能直接把path给push进去,因为push进去的是地址
// 而之后path会被清空,所以不能直接push
res.push([...path])
return;
}
for(let item of nums) {
// 因为这里路径不允许重复,所以如果存在就下一步
if(path.includes(item)) {
continue
}
path.push(item)
backtrack(nums, path)
path.pop()
}
}
backtrack(nums, path)
return res
}
b、N皇后
给一个N*N的棋盘,放置N个皇后,使任意两个皇后不能在同一行、同一列、同一对角(左上、左下、右上、右下)
// n指棋盘的n行n列n皇后
function queen(n) {
let res = []
// 先把n*n的棋盘初始化
let path = new Array(n)
for(let i = 0; i < n; i++) {
path[i] = new Array(n).fill(false)
}
let backTrace = function(row, path) {
// 如果有n行了就可以停止了
if(path.length === row) {
// 二维数组深克隆要注意
res.push([JSON.parse(JSON.stringify(path))])
return
}
for(let i = 0; i < n; i++) {
if(!isValid(row, i, path)) {
continue
}
// [row, j]表示[行, 列]
path[row][i] = true
backTrace(row + 1, path)
path[row][i] = false
}
}
backTrace(0, path)
return res
}
// 是否可以放皇后,true可以放,false不可以放
function isValid(row, col, path) {
// 如果当前是第一行,就可以直接返回true
if(row === 0) {
return true
}
// 目前要判断的左上,同列,右上有皇后,这一个就不能放
// 同列
for(let i = 0; i < row; i++) {
if(path[i][col]) {
return false
}
}
// 左上角
for(let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if(path[i][j]) {
return false
}
}
// 右上角
for(let i = row - 1, j = col + 1; i >= 0 && j < path.length; i--, j++) {
if(path[i][j]) {
return false
}
}
return true
}
c、戳气球伪代码
题目见动态规划
function balloon(arr) {
let res = 0
let path = [...arr]
let backTrace = function(path, score) {
if(path.length === 0) {
res = Math.max(score, res)
return
}
for(let i = 0; i < path.length; i++) {
let left = right = 1
if(i - 1 >= 0) {
left = path[i - 1]
}
if(i + 1 < path.length) {
right = path[i + 1]
}
let newScore = left * path[i] * right + score
let temp = path[i]
// Array.prototype.splice()
// 第一个参数是开始下标,第二个是删除个数(如果是0或负数就不删除),第三个是增加的值
path.splice(i, 1)
backTrace(path, newScore)
path.splice(i, 0, temp)
}
}
backTrace(path, 0)
return res
}
但是回溯是暴力拆题,所以时间复杂度不太好,空间复杂度也是
5)分支界定
2、其他算法题
1、括号匹配问题
https://leetcode-cn.com/problems/valid-parentheses/
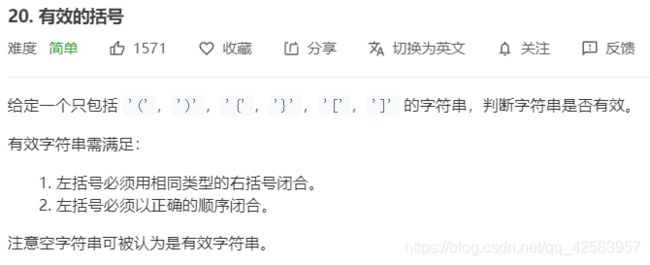
使用栈,如果为左括号就入栈,如果碰到右括号就跟栈顶比较,若是一对,出栈
const pairs = [['(', ')'], ['{', '}'], ['[', ']']];
function isAllPairsValid(str) {
let arr = []
for(let i = 0; i < str.length; i++) {
for(let j = 0; j < pairs.length; j++) {
if(str[i] === pairs[j][0]) {
arr.push(str[i])
}
if(str[i] === pairs[j][1]) {
if(arr[arr.length - 1] === pairs[j][0]) {
arr.pop()
}else {
return false
}
}
}
}
return true
}
// test
console.log(isAllPairsValid('(([)]')) // false
console.log(isAllPairsValid('[((test)foo)]{bar}{hey}')) // true
console.log(isAllPairsValid('([)]')) // false
括号匹配的进阶版

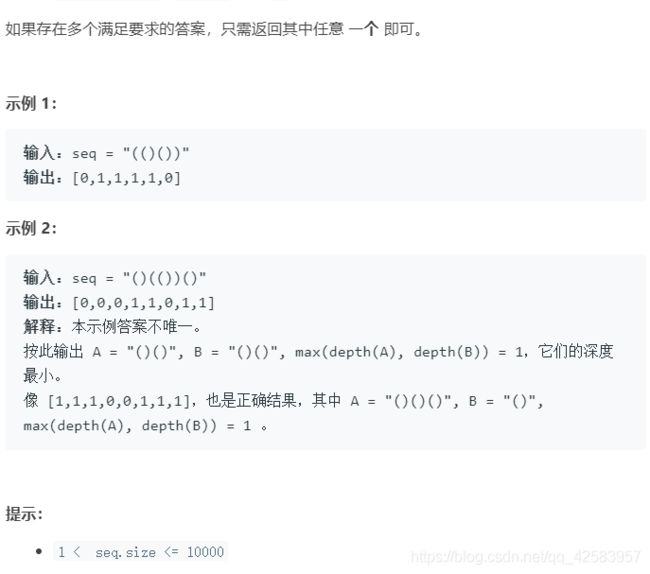
这个题目老实说,很难,主要是题目读不懂的难,在题目读不懂的情况下我们可以从示例入手
/**
* @param {string} seq
* @return {number[]}
*/
var maxDepthAfterSplit = function(seq) {
let stack = []
if(seq.length === 0) {
return 0
}
let res = []
for(let i = 0; i < seq.length; i++) {
if(seq[i] === '(') {
stack.push(seq[i])
res[i] = stack.length % 2 ? 0 : 1
} else {
res[i] = stack.length % 2 ? 0 : 1
stack.pop()
}
}
return res
};
/**
* @param {string} s
* @return {number}
*/
var longestValidParentheses = function(s) {
let stack = [-1]
let max = 0
for(let i = 0; i < s.length; i++) {
if(s[i] === '(') {
stack.push(i)
} else {
// 去掉(
stack.pop()
if(stack.length === 0) {
// 说明不是有效括号,入栈
stack.push(i)
} else {
// 计算最后一个括号和留下的最后一个不是括号的
max = Math.max(max, i - stack[stack.length - 1])
}
}
}
return max
};
2、双指针问题
双指针问题主要有两方面,分为快慢指针和左右指针
快慢指针主要针对链表,如链表是否有环
左右指针主要针对数组或字符串,如二分查找
快慢指针
a、链表是否问题:
主要是设置两个指针,快指针比满指针步长多1,如果没有环,快指针会遇到null,如果有环,快指针和满指针会相遇
function hasCircle(head) {
let slow = fast = head
while(fast !== null & slow !== null) {
fast = fast.next.next
slow = slow.next
if(slow === fast) return true
}
return false
}
b、链表环的起始位置问题
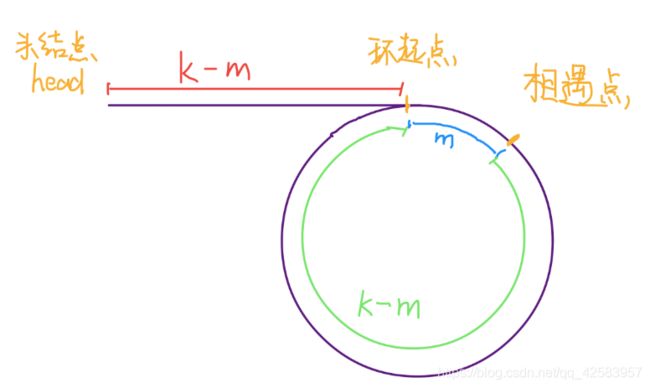
已知链表有环,求环的起始位置
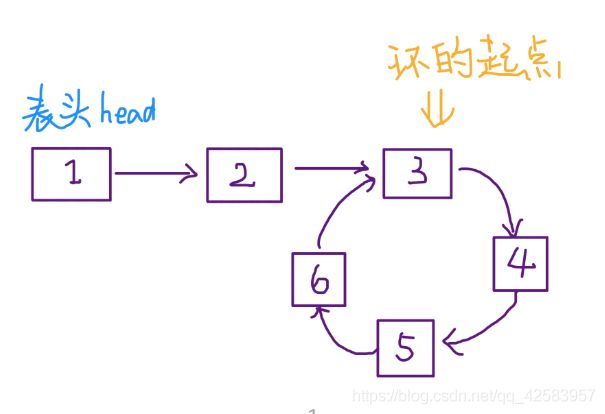
假设在某点相遇,此时快指针走了2k步,慢指针走了k步
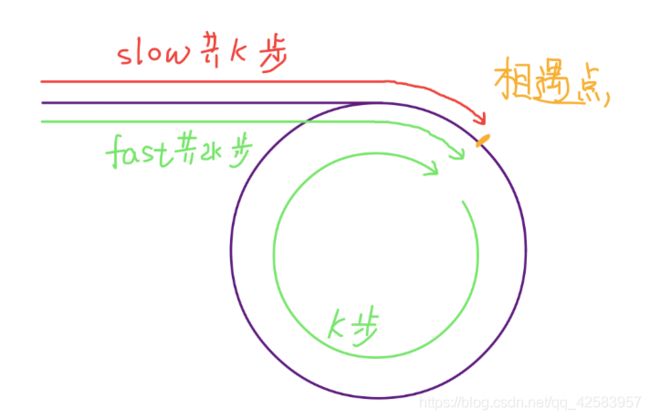
若把慢指针或快指针中的一个设为头指针,然后快慢指针一起前进,最后相遇的点就是环的初始位置,因为他们都走了k-m
function start(head) {
let slow = fast = head
while(slow !== null && fast !== null) {
slow = slow.next
fast = fast.next.next
if(fast === slow) break
}
slow = head
while(slow !== fast) {
slow = slow.next
fast = fast.next
}
return slow
}
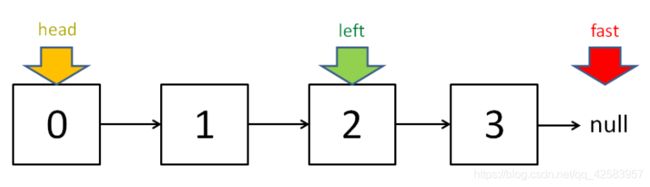
c、寻找无环链表的中步
可以通过让快指针走两步,慢指针走一步,当快指针走到终点的时候,满指针就走到中间了
function findMid(head) {
let slow = fast = head
while(slow !== null && fast !== null) {
slow = slow.next
fast = fast.next.next
}
return slow
}
d、寻找链表倒数第k个
这个的思路是让快指针先走k步
然后让快慢指针都同时走1步,当快指针到null后,满指针指向的就是第k个
function findLastK(head, k) {
let fast = slow = head
for(let i = 0; i < k; i++) {
if(fast === null) {
return fasle
}
fast = fast.next
}
while(fast !== null && slow !== null) {
fast = fast.next
slow = slow.next
}
return slow
}
/**
* @param {number[]} nums
* @return {number}
*/
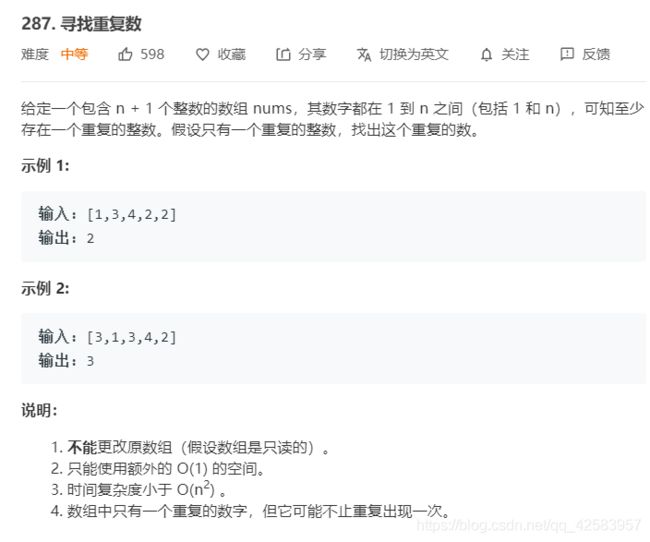
var findDuplicate = function(nums) {
let slow = 0,fast = 0
do {
slow = nums[slow]
fast = nums[nums[fast]]
} while (slow !== fast)
slow = 0
while(slow !== fast) {
slow = nums[slow]
fast = nums[fast]
}
return slow
};
这道题其实用快慢指针是特别方便的,而看出它需要使用快慢指针也是特别重要的,根据这道题,我们可以总结出什么情况下需要使用快慢指针
①当值或其他什么可以作为下标的时候,且永远不会回到0号下标(因为我们知道快慢指针通常用来解决有环问题,而很多时候不会明确告诉你有环,那么什么时候有环呢?只要有重复)
②我们把某个重复的值就作为环开始的地方,需要求这个地方就用快慢指针
③快慢指针不一定只适合于链表,数组等顺序结构也是可以用的
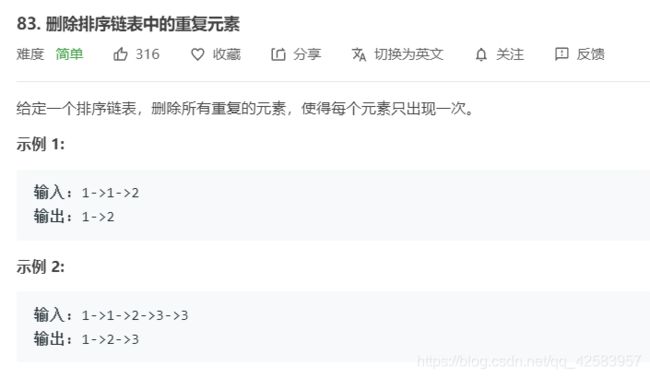
f、删除链表重复元素
这一道题最主要的是要注意慢指针在遇到重复元素后不移动,而快会诊要移动
var deleteDuplicates = function(head) {
if(head === null) {
return null
}
let slow = head, fast = head.next
while(fast !== null && slow !== null) {
if(fast.val === slow.val) {
slow.next = fast.next
if(fast.next !== null) {
fast.next = slow.next
} else {
fast.next = null
}
fast = fast.next
} else {
slow = slow.next
fast = fast.next
}
}
return head
};
除此之外,这道题也可以使用循环
var deleteDuplicates = function(head) {
let node = head
while(node !== null && node.next !== null) {
if(node.val === node.next.val) {
node.next = node.next.next
} else {
node = node.next
}
}
return head
};
左右指针
a、二分查找
function binarySearch(arr, value) {
let left = 0, right = arr.length - 1
while(left <= right) {
let mid = left + Math.ceil((right - left) / 2)
if(arr[mid] === value) {
return mid
} else if(arr[mid] > value) {
left = mid + 1
} else if(arr[mid] < value) {
right = mid - 1
}
}
return -1
}
function sum(arr, value) {
let left = 0, right = arr.length - 1
while(left < right) {
let sum = arr[left] + arr[right]
if(sum === value) {
// 因为题目要求索引从1开始
return [left + 1, right + 1]
} else if(sum < value) {
left++
} else if(sum > value) {
right--
}
}
return [-1, -1]
}
c、数组反转
function reverse(arr) {
let left = 0, right = arr.length - 1
while(left < right) {
let temp = arr[left]
arr[left] = arr[right]
arr[right] = temp
left++;
right--;
}
return arr
}
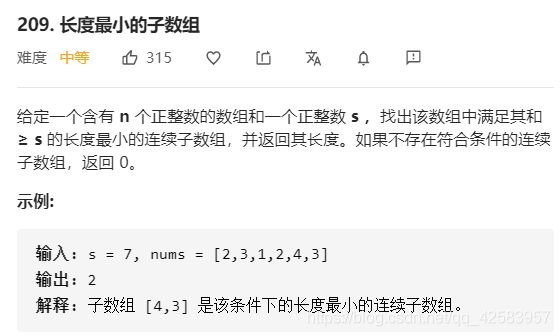
d、滑动窗口
说白了就是维护一个窗口,然后不断移动窗口边界,最后取出窗口里的数据
a)、最小覆盖子串

先分析一下这道题,首先,他只是要找T中所有字母,也就是说T=‘ABC’,S=‘BAC’这种顺序不同的也可以,不要求顺序,只要有那个字母就OK
同理,如果T=‘AABC’,还是找有两个A,一个B,一个C的串
而且因为要求的是子串,所以找到的这几个字母一定是连续的
具体原理就是,先移动右指针,直到找到一个能包含所有需要字符的串(右边的最后一个一定是需要的字符)
然后移动左指针,看到哪一步就不能再动了(其实就是移动到第一个能匹配上的就不能动了)
但是又因为有可能在右指针后面还有能匹配上的,而且能组成最小匹配子串,所以移动右指针这个东西应当是外层循环,终止条件是到达s字符串末尾
另外这是左开右闭即 [left, right) 的,所以需要把最开始的那一个放进去
function sliderWindow(s, t) {
// left 和 right 是s的左右指针
let left = 0, right = 0
let need = {}, sliWindow = {}
// start是最小覆盖子串开始的下标,valid是指满足need条件的字符个数
let start = 0, valid = 0
// len指的是最小覆盖子串的长度
let len = Number.MAX_VALUE
// 初始化
for(let item of t) {
if(need[item]) {
need[item]++
} else {
need[item] = 1
sliWindow[item] = 0
}
}
while(right < s.length) {
// 窗口数据的一系列更新
// s[right]就是当前指针的字符
let now = s[right]
// 扩大窗口
// 因为这个其实是左开右闭,所以最开始窗口里什么都没有
right++
// need[s[right]]可以看是否需要这个字符
if(need[now]) {
// 需要就存进window
sliWindow[now]++
// 如果窗口里有需要的就更新valid
if(sliWindow[now] === need[now]) {
valid++
}
}
// 看窗口是否要通过移动左边的指针来收缩窗口
// 如果窗口大小跟要求的t的长度相等就得收缩
while(valid === t.length) {
// 只要能找到更小的子串个数,就更新start和len
if(right - left < len) {
start = left
len = right - left
}
// 记录一下将要移出窗口的值
let temp = s[left]
// 移动左指针,看能不能找到小的
left++
// 看一下之前移出的是不是也能匹配上
// 如果能匹配上,就把之前放到window里的减去一个
// 并把valid--
if(need[temp]) {
if(sliWindow[temp] === need[temp]) {
valid--
}
sliWindow[temp]--
}
}
}
return len === Number.MAX_VALUE ? '' : s.slice(start, start + len)
}
function display(str1, str2) {
let left = 0, right = 0
let valid = 0
let slideWindow = {}, need = {}
let len = Number.MAX_VALUE
for(let i of str1) {
if(need[i]) {
need[i]++
} else {
need[i] = 1
slideWindow[i] = 0
}
}
while(right < str2.length) {
let c = str2[right]
right++
if(need[c]) {
slideWindow[c]++
if(slideWindow[c] === need[c]) {
valid++
}
}
while(valid === str1.length) {
if(right - left < len) {
len = right - left
}
let temp = str2[left]
left++
if(need[temp]) {
if(need[temp] === slideWindow[temp]) {
valid--
}
slideWindow[temp]--
}
}
}
return len === str1.length
}
function find(str1, str2) {
let left = 0, right = 0
let start = 0, len = Number.MAX_VALUE
let valid = 0
let slideWindow = {}, need = {}
let res = []
for(let item of str2) {
if(need[item]) {
need[item]++
} else {
need[item] = 1
slideWindow[item] = 0
}
}
while(right < str1.length) {
let c = str1[right]
right++
if(need[c]) {
slideWindow[c]++
if(slideWindow[c] === need[c]) {
valid++
}
}
while(valid === str2.length) {
if(right - left <= len) {
start = left
len = right - left
}
let temp = str1[left]
left++
if(need[temp]) {
if(need[temp] === slideWindow[temp]) {
valid--
}
slideWindow[temp]--
}
if(len === str2.length && !res.includes(start)) {
res.push(start)
}
}
}
return res
}
function find(str) {
let left = 0, right = 0
let slideWindow = {}
let res = 0
while(right < str.length) {
let c = str[right]
right++
if(slideWindow[c]) {
slideWindow[c]++
} else {
slideWindow[c] = 1
}
// 看拓宽右边的同时左边是否要收缩
while(slideWindow[c] > 1) {
let temp = str[left]
left++
slideWindow[temp]--
}
res = Math.max(res, right - left)
}
return res
}
3、单调栈问题
首先,单调栈是一个特别的数据结构,说白了也是栈,只不过入栈的数据都是有顺序的(升序或降序)
这里主要使用单调栈来解决环形数组
a、求距离最近的大数/小数
问:给一个数组,返回一个等长的数组,返回数组每个值代表比原数组这个下标元素值a更大的值b,且b的下标要大于a的下标,若没有则该元素返回-1
相当于[2, 1, 2, 4, 3],返回结果为[4, 2, 4, -1, -1]
就相当于排队,第一高的把后面的挡到了,就不需要管后面矮的了
从后往前入栈,只要倒数第n+1个比倒数第n个高,把倒数第n个及n-1,n-2之类的出栈,倒数第n+1进栈

function find(arr) {
let res = new Array(arr.length).fill(-1)
let temp = []
for(let i = arr.length - 1; i >= 0; i--) {
// 把放进栈里小于前面数的都清掉,毕竟就算再要更前面的数时
// 前面已经有大的了,也不会看后面的
while(temp.length !== 0 && temp[temp.length - 1] <= arr[i]) {
temp.pop()
}
res[i] = temp.length === 0 ? -1 : temp[temp.length - 1]
temp.push(arr[i])
}
return res
}
虽然我这里用了一个 for 循环和一个 while 循环,但是其实实际上一个数也顶多入栈一次,出栈一次,也就是说时间复杂度不为O(n2),而是O(n)
一个变形
给你一个数组 T = [73, 74, 75, 71, 69, 72, 76, 73],这个数组存放的是近几天的天气气温。返回一个数组,计算:对于每一天,你还要至少等多少天才能等到一个更暖和的气温;如果等不到那一天,填 0 。
function find(arr) {
let res = []
let temp = []
for(let i = arr.length - 1; i >= 0; i--) {
while(temp.length !== 0 && temp[temp.length - 1][0] <= arr[i]) {
temp.pop()
}
res[i] = temp.length === 0 ? 0 : temp[temp.length - 1][1] - i
// [值,下标]
temp.push([arr[i], i])
}
return res
}
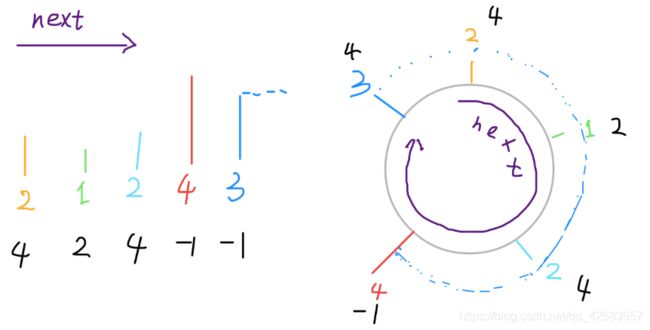
b、循环数组
同样是求最近距离的,依旧给一个数组[2, 1, 2, 4, 3],但是因为首尾相连,所以结果为[4,2,4,-1,4]
首先明确一下,计算机是线性结构,没有真正意义上的环形数组,一般情况下的环形数组,要实现就是通过 % 取模得到的
我们看一下这道题,如果给的是一个环形数组,要求结果,依旧是使用比身高,如图
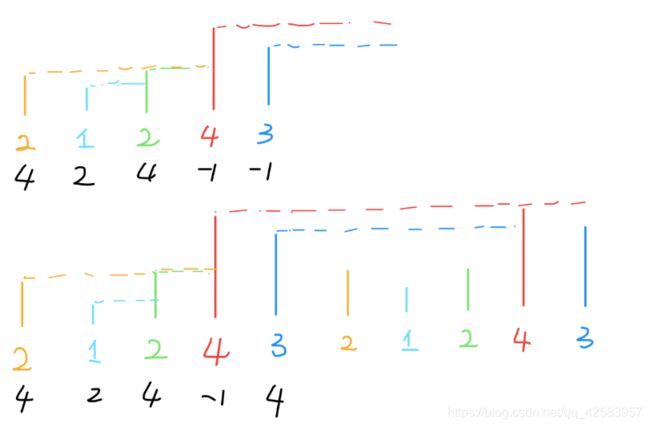
这里解决方法其实有两种,第一个是把数组再复制一次得到一个新数组,新数组依旧用原来的方法,最后得到的结果截取一半使用即可
这里的话采用的是循环数组的特性(也就是%取模来做)
function find(arr) {
let res = [], temp = []
let len = arr.length
// 假装把这个数组复制了一份
for(let i = len * 2 - 1; i >= 0; i--) {
while(temp.length !== 0 && arr[i % len] >= temp[temp.length - 1]) {
temp.pop()
}
res[i % len] = temp.length === 0 ? -1 : temp[temp.length - 1]
temp.push(arr[i % len])
}
return res
}
4、二叉树
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var preorderTraversal = function(root) {
let res = []
let traversal = function(root) {
if(root) {
res.push(root.val)
traversal(root.left)
traversal(root.right)
}
}
traversal(root)
return res
};
非递归的迭代解法:
var preorderTraversal = function(root) {
let res = []
let stack = []
while(root !== null || stack.length !== 0) {
while(root !== null) {
res.push(root.val)
stack.push(root.right)
root = root.left
}
root = stack.pop()
}
return res
};
b、中序遍历
递归
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var inorderTraversal = function(root) {
let res = []
let traversal = function(root) {
if(root) {
traversal(root.left)
res.push(root.val)
traversal(root.right)
}
}
traversal(root)
return res
};
迭代
var inorderTraversal = function(root) {
let res = []
let stack = []
while(root !== null || stack.length !== 0) {
while(root !== null) {
stack.push(root)
root = root.left
}
root = stack.pop()
res.push(root.val)
root = root.right
}
return res
};
c、后序
递归版
var postorderTraversal = function(root) {
let res = []
let find = function(root) {
if(root === null) {
return null
}
find(root.left)
find(root.right)
res.push(root.val)
}
find(root)
return res
};
非递归版
var postorderTraversal = function(root) {
let res = []
let stack = []
while(root !== null || stack.length !== 0) {
while(root !== null) {
stack.push(root)
root = root.left === null ? root.right : root.left
}
root = stack.pop()
res.push(root.val)
// 这里是假设该节点有左节点,则该节点为根节点,应该先遍历该节点的右节点
if(stack.length !== 0 && stack[stack.length - 1].left === root) {
root = stack[stack.length - 1].right
} else {
// 否则就代表这个节点之前已经遍历了右节点,直接把这个根节点拿到即可
root = null
}
}
return res
};
然后我们来总结一下关于树的遍历模板(非迭代方法)
首先树的三种遍历其实都是DFS,一般情况下我们都知道DFS经常和回溯在一起,且DFS经常是递归实现的,所以这里用递归肯定很简单
而使用迭代其实掌握到模板也很简单
DFS使用的主要的数据结构就是栈(因为先进后出),来记录走过的路
function traversal(root) {
// 结果
let res = []
// 定义一个栈,储存之前走过的路
let stack = []
// 要继续得到结果的条件,肯定是该节点不为空,或者当前栈中还有东西没遍历完
// 另外,无论是先序、中序还是后序这个条件都是相同的
while(stack.length !== 0 || root !== null) {
// 这个条件是什么时候应该入栈(存储过往路径)
// 无论先序、中序、后序都是这个条件
while(root !== null) {
// 什么时候入栈,什么时候移动root
// 入栈的是什么,自身(中序和后序)还是右边(先序)
// 以及怎么移动,向左(先序和中序)还是向右(后序其实是左右判断)
}
// 把之前储存的拿出来
root = stack.pop()
// 保存结果
res.push(root.val)
// 是要继续往右吗(中序和后序),有条件吗(后序有条件),条件是什么
}
return res
}
var levelOrder = function(root) {
if(root === null) return []
let res = []
let queue = [root]
while(queue.length !== 0) {
let value = []
let size = queue.length
// 重点,这是能够得到哪儿一层的
for(let i = 0; i < size; i++) {
root = queue.shift()
value.push(root.val)
if(root.left !== null) {
queue.push(root.left)
}
if(root.right !== null) {
queue.push(root.right)
}
}
res.push(value)
}
return res
};
e、通过中序遍历和后序遍历找一棵树
首先后序遍历的最后一个元素一定是根,而在中序遍历中这个元素的左边是左子树,右边是右子树,再放到后序遍历中通过个数找到左子树和右子树,再求最后一个是根,这样循环
var buildTree = function(inorder, postorder) {
let find = function(inorder, postorder) {
if(inorder.length === 0 || postorder.length === 0) {
return null
}
let root = postorder[postorder.length - 1]
let index = inorder.indexOf(root)
let node = new TreeNode(root)
node.left = find(inorder.slice(0, index), postorder.slice(0, index))
node.right = find(inorder.slice(index + 1), postorder.slice(index, -1))
return node
}
return find(inorder, postorder)
};
f、从前序与中序遍历序列构造二叉树
前面讲了后序和中序,这个前序和中序其实也差不多,只是根出现的位置问题,所以直接上代码
var buildTree = function(preorder, inorder) {
let find = function(preorder, inorder) {
if(preorder.length === 0 || inorder.length === 0) {
return null
}
let root = preorder[0]
let index = inorder.indexOf(root)
let node = new TreeNode(root)
node.left = find(preorder.slice(1, index + 1), inorder.slice(0, index))
node.right = find(preorder.slice(index + 1), inorder.slice(index + 1))
return node
}
return find(preorder, inorder)
};
g、填充每个节点的下一个右侧节点指针
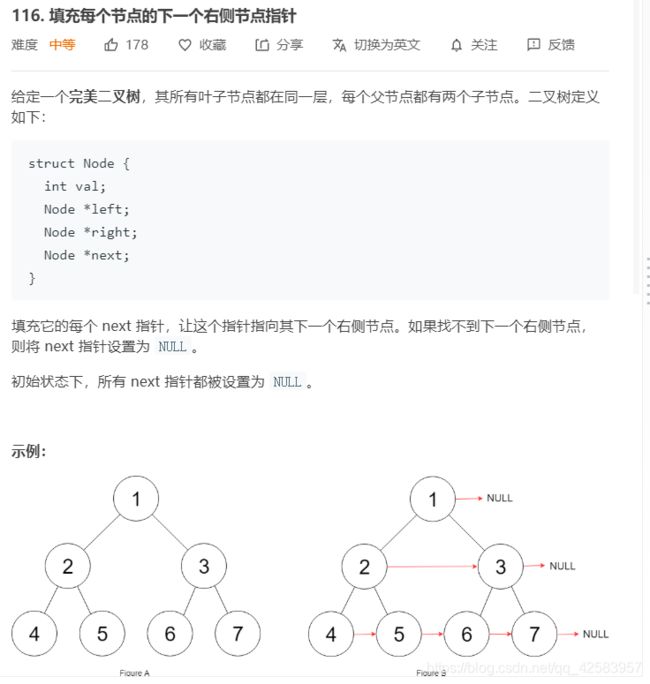
这道题的巧妙之处在于利用了完美二叉树,而且让递归函数的参数不是一个
var connect = function(root) {
let find = function(node, next) {
if(node === null) {
return
}
node.next = next
find(node.left, node.right)
find(node.right, node.next === null ? null : node.next.left)
}
find(root, null)
return root
};
h、填充每个节点的下一个右侧节点指针 II
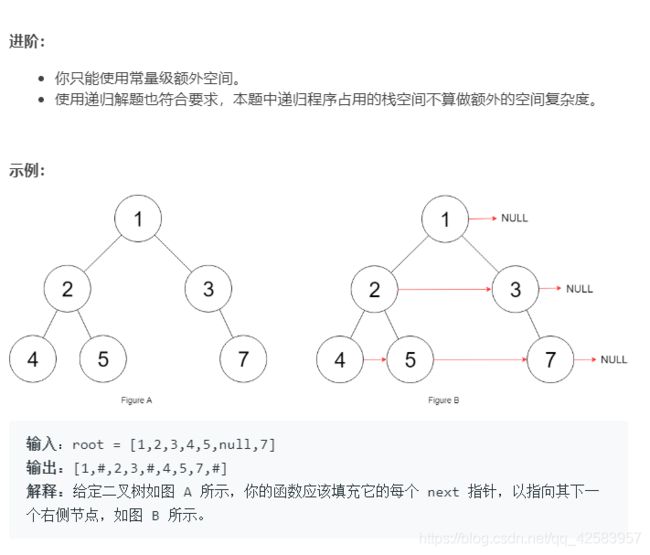
然后进阶版,非完美二叉树
不多说,其实就是完美二叉树多了几种判断情况,具体见代码吧
var connect = function(root) {
let find = function(node) {
if(!node || (!node.left && !node.right)) {
return node
}
if(node.left && node.right) {
node.left.next = node.right
node.right.next = getNode(node)
} else if(node.left) {
node.left.next = getNode(node)
} else if(node.right) {
node.right.next = getNode(node)
}
node.right = find(node.right)
node.left = find(node.left)
return node
}
let getNode = function(node) {
while(node.next) {
if(node.next.left) {
return node.next.left
}
if(node.next.right) {
return node.next.right
}
node = node.next
}
}
return find(root)
};
i、二叉树的最近公共祖先


其实遇到二叉树,就要先思考,使用哪种遍历,我们这里是找公共祖先的,所以很自然的能想到是从底向上,而从底向上的遍历最显著的就是后序遍历(先序遍历是自顶向下),确认了使用后序后,我们这里采用递归,就把后序遍历改写一下就可以了
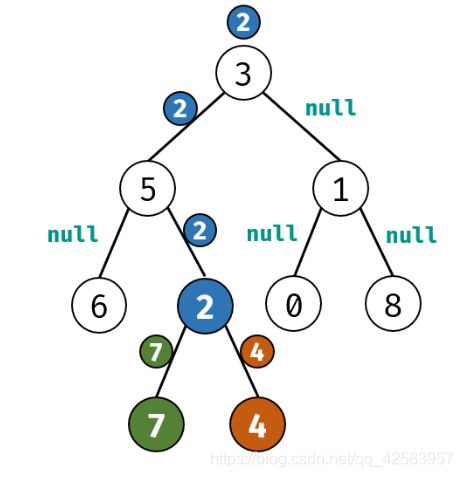

var lowestCommonAncestor = function(root, p, q) {
let find = function(root) {
if(!root || root === p || root === q) {
return root
}
let left = find(root.left)
let right = find(root.right)
if(!left && !right) {
return null
} else if(!left) {
return right
} else if(!right) {
return left
}
return root
}
return find(root)
};
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* Encodes a tree to a single string.
*
* @param {TreeNode} root
* @return {string}
*/
var serialize = function(root) {
let queue = [root]
let res = []
while(queue.length !== 0) {
root = queue.shift()
if(root !== null) {
queue.push(root.left)
queue.push(root.right)
}
if(root) {
res.push(root.val)
} else {
res.push(null)
}
}
return res.toString()
};
/**
* Decodes your encoded data to tree.
*
* @param {string} data
* @return {TreeNode}
*/
var deserialize = function(data) {
let arr = data.split(',')
console.log(arr)
if(arr.length === 0 || arr[0] === '') {
return null
}
let tree = new TreeNode(arr.shift())
let node
let queue = [tree]
while(arr.length !== 0) {
node = queue.shift()
while(node === null) {
node = queue.shift()
}
if(node === undefined) {
return tree
}
let num = arr.shift()
node.left = (num ? new TreeNode(num) : null)
num = arr.shift()
node.right = (num ? new TreeNode(num) : null)
queue.push(node.left, node.right)
}
return tree
};
/**
* Your functions will be called as such:
* deserialize(serialize(root));
*/
5、Map
![]()
这一道题其实最开始应该首先是想到object的,但是object是无序的,同理,set也是无序的,所以我们可以自然而然地想到map,在js中map是根据插入顺序来的,这里跟java不同(java的map无序,hashMap根据hashcode排序跟object差不多)
这里引申两个知识点
map和set的共同点和区别
关于共同点:
1、都是ES6提出的
2、都不允许重复关于不同点:
1、map是根据插入顺序来排序的(FIFO),而set无序
2、map是键值对,set只有值
map和object的区别:
1、map有序,object按照key的字典码排序(所以是无序的)
2、map的key可以是任何值,object的key只能是symbol或字符串
3、map的长度可以通过Map.prototype.size得到,而object只能自己算
然后我们再来讲讲 页面置换算法(这东西可以在操作系统里看到)
页面置换算法:当要访问某页面,但是内存不够时,就会将内存中的某一页面替换成新的页面,计算到底是哪儿个页面被置换出去的算法就叫做页面置换算法
如果算法不够好,有可能刚换出去的页面又要被换进来,这种情况叫做抖动(把时间都浪费在置换页面上了)
这里主要介绍4种页面置换算法
其中有两种极端:
①最佳置换算法
相当于看一下现在放在页面区域的页码哪个越靠后或者没有在后面被使用的就置换出去
②FIFO置换算法
这个就相当于队列,先进先出,没有考虑过之后是否使用这种,所以这也是最坏的置换方法③LRU置换算法(又称最久未被使用的页面置换方法)
望文生义,把储存的页面中最少被使用的给置换出去
但其实这个的实现方法是有一个栈,然后把使用了的从栈的某个位置拿出,放到栈底,而如果需要置换的时候直接从栈顶拿就行
④LFU页面置换算法(最少使用)
给每个页面计数,如果使用的次数少就被置换出去
/**
* @param {number} capacity
*/
var LRUCache = function(capacity) {
// 为什么用map而不用object,map有序,按照插入的顺序
this.stack = new Map()
this.stack.clear()
this.capacity = capacity
};
/**
* @param {number} key
* @return {number}
*/
LRUCache.prototype.get = function(key) {
if(this.stack.has(key)) {
let value = this.stack.get(key)
this.stack.delete(key)
this.stack.set(key, value)
return value
} else {
return -1
}
};
/**
* @param {number} key
* @param {number} value
* @return {void}
*/
LRUCache.prototype.put = function(key, value) {
if(!this.stack.has(key)) {
if(this.capacity === this.stack.size) {
let popKey = this.stack.keys().next().value
this.stack.delete(popKey)
}
} else {
this.stack.delete(key)
}
this.stack.set(key, value)
};
/**
* Your LRUCache object will be instantiated and called as such:
* var obj = new LRUCache(capacity)
* var param_1 = obj.get(key)
* obj.put(key,value)
*/
6、前缀和
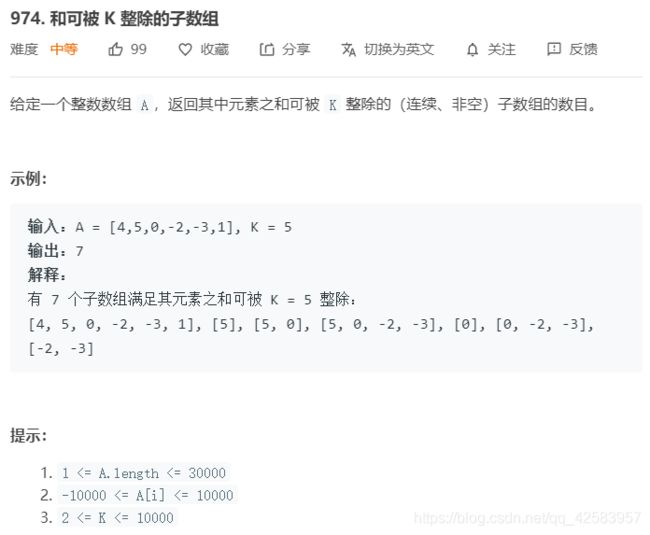
首先这里的子数组,就其实类似于子串,毕竟子串和子数组都是紧挨着的,而子序列是不需要紧挨的

/**
* @param {number[]} A
* @param {number} K
* @return {number}
*/
var subarraysDivByK = function(A, K) {
// res[i]表示最后%k的值为i的子数组个数
let res = new Array(K).fill(0)
// 初始的应该为1
// 毕竟最开始和为0,0%k===0
res[0] = 1
// sum指前n项的和%k
let sum = 0
// 表示能被整除的总共的次数
// 为什么这里又是1呢,毕竟要的是子数组,子数组里不能为空嘛
// 所以把最开始的那个去掉
let count = 0
for(let i = 0; i < A.length; i++) {
sum += A[i]
sum %= K
// 这里要考虑如果有负会怎么样,因为是mod后依旧有负数,所以加一个K就能变成正的
// 不能用负数,毕竟没有负数的下标
if(sum < 0) {
sum += K
}
count += res[sum]
res[sum]++
}
return count
};
7、正则表达式
/**
* @param {string} s
* @return {string}
*/
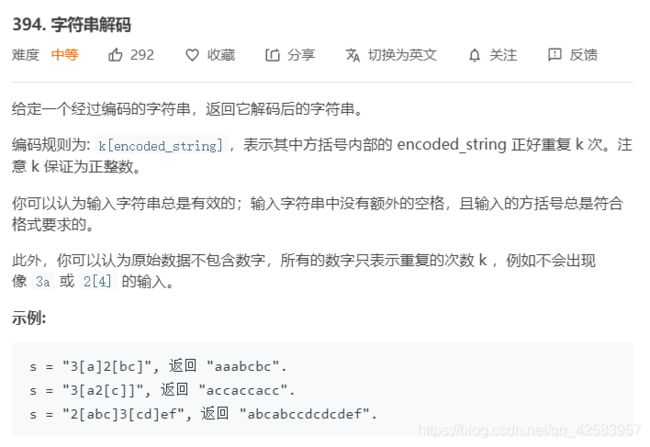
var decodeString = function(s) {
let regex = /(\d+)\[(\w+)\]/
while(regex.test(s)) {
// String.prototype.repeat(n)可以重复这个字符串n次
s = s.replace(regex, RegExp.$2.repeat(RegExp.$1))
}
return s
};
代码放完,我们来重温一下正则表达式
首先,正则表达式对象是 RegExp,我们在本题中有了子匹配,而子匹配就是存在 RegExp 中的以 $1、$2 等的属性
这里有个很重要的一点,那就是子匹配的 $1、$2会被覆盖! 所以我们的正则匹配里不能写成全局的(也就是 g)
所以我这里使用了 RegExp.prototype.test 来循环
以上为根据这道题延伸出来的正则
接下来系统地说一下正则
以上叫做匹配元字符,除了这个还有匹配修饰符,如下

匹配范围:

我们可以看出如果字符串中有**[]、()、|、-**这些,就必须加斜杠(\)进行转义
说到转义,因为通过 RegExp 构造函数时也要转义,就相当于如果直接用字面量 /[a-z]\s/i 和使用构造函数 new RegExp("[a-z]\\s", "i") 是一样的
而 /[a-z]:\\/i 和 new RegExp("[a-z]:\\\\","i") 是一样的
相当于构造函数的斜杠是字面量的两倍
除此之外还有量词

如果只有元字符,没有量词,那么那个元字符代表的必须出现且只能出现一次,而加上量词后出现次数由量词决定
除了以上的,还有一些特殊的字符如
^:以什么开头
$:以什么结尾
.:任意单个字符


然后我们再来看看使用正则表达式的方法(都是 RegExp.prototype 上的)

而字符串的方法主要是两个,search和replace

8、单调栈
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
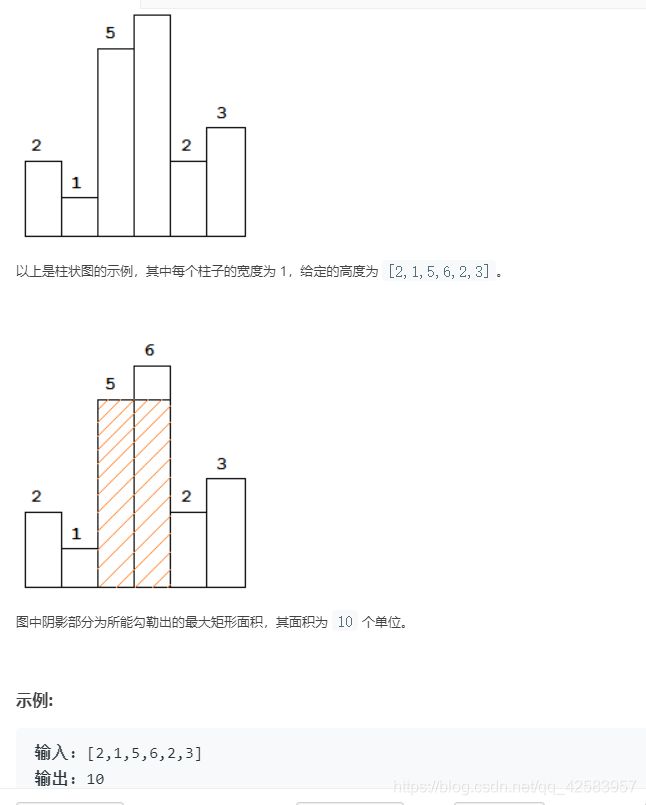
先谈谈这道题的基本思路,首先我们要求面积,那么就可以很自然的想到公式面积=宽*高,而在这里面高是最好得到的,就是heights[i],而宽的话要求到就需要一点技巧
因为我们最开始是不知道要怎么求到宽的,所以最先就想到暴力解法,如图
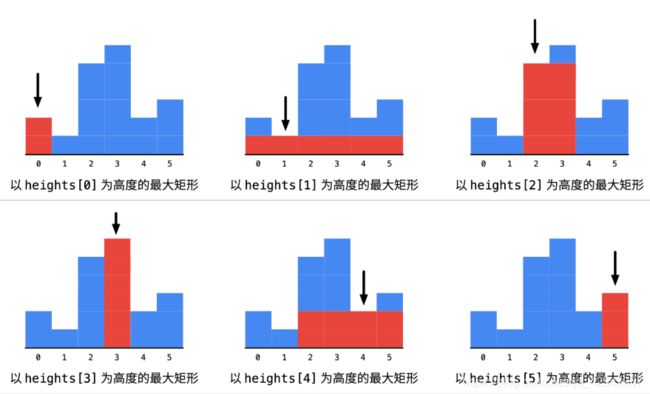
然后我们就可以找到规律,如果后面的那根柱子比当前的高,那么宽度就不能向后继续延伸,如果前面某根柱子比当前的高,宽度也不能继续向前延伸,也就是如下所示
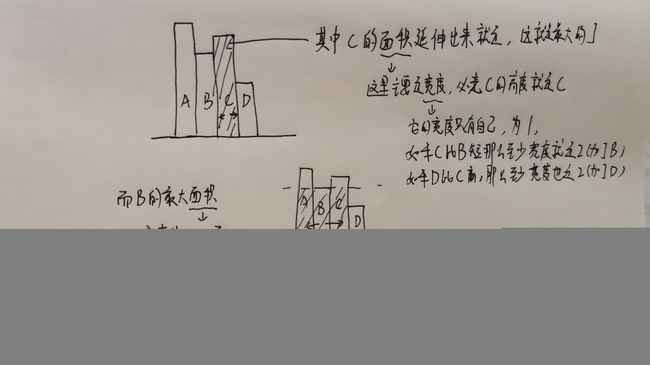
我们要找左边一个什么什么怎么怎么样,右边什么什么怎么怎么样,很自然就能想到用栈(这里可以回忆一下之前求括号那个题,就跟求括号一样,后面的结果会引起前面结果计算完成,也可能要等到很后面的结果才能使前面能计算到结果),所以用栈
好了,接下来我们想想栈的条件,我们可以很清楚地发现当我们拿到某个heights[i]且当这个heights[i]比heigths[i - 1]小时,它是能决定前面是已经得到后面的边界了,这样我们就可以推出,放在栈里的应该是比后一个小的,而如果每一个都比后一个小,那么这个栈应当是单调递增栈
单调递增栈出来了,现在就应该考虑进栈的元素是什么,因为我们要的是宽度,宽度与下标有关,所以下标进栈
其他具体的我们从代码上来看
/**
* @param {number[]} heights
* @return {number}
*/
var largestRectangleArea = function(heights) {
// 为什么要在头尾都各加一根长度为0的柱子
// 我们这里想想,我们是什么时候会进行计算max?
// 当后面的柱子比我们放在栈顶的柱子低的时候就要计算
// 那么如果我们不在尾巴上添加一根为0的柱子(毕竟没有为负的),怎么才能计算到最后一根柱子的max呢
// 毕竟这里的max其实是每个柱子的max最后取的最大值
// 至于在头加一个0,是为了方便,这样下标就表示是第几根柱子
heights = [0, ...heights, 0]
// 这里的arr[i] = n,n表示这是第几个柱子
let arr = []
let max = 0
for(let i = 0; i < heights.length; i++) {
// 只有当新判断的下标比栈顶高时才进行入栈和计算面积操作
// 一般判断这种的就得先看一下栈是否为空
// 关于为什么这里比较的是栈顶,而不是heights[i - 1]
// 我们每次在最后都会把i给push到栈顶,就相当于是下一轮的i-1
// 所以如果是第一次的话其实这个就是栈顶,直接写heigths[i - 1]也是可以的
// 但是毕竟我们是循环,要出栈的,而heigths[i-1]和heights[i]都是恒变量
// 一直比较不能作为终止条件
while(arr.length !== 0 && heights[arr[arr.length - 1]] > heights[i]) {
// 毕竟while的条件是要后面比栈顶矮
let index = arr.pop()
// 毕竟要求的面积是前一个柱子的
// 至于为什么宽是i - (栈顶 + 1)
max = Math.max(max, (i - (arr[arr.length - 1] + 1)) * heights[index])
}
arr.push(i)
}
return max
};
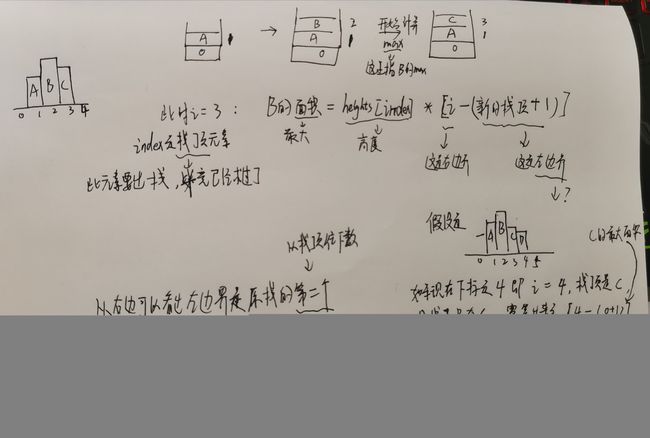
关于这个的时间复杂度,感觉上可能跟暴力解法差不多,都是O(n2)的样子,但实际上不是,毕竟进栈和出栈都只有一次,所以时间复杂度应该是O(n)
9、对称二叉树
![]()
首先,镜像对称就相当于人的左手=人的右手,也就是说左节点的左孩子=右节点的右孩子,左节点的右孩子=右节点的左孩子
另外,我们要明确,我们比较的时候是从上往下比,如果父节点都不同,那就没必要比较子节点
我们这里先使用递归,所以要找到终止条件,条件很好找,因为我们比较的是左右节点的左右孩子,传进去的参数就是两个节点(两个孩子),所以只要这两个节点都为空,则正确,若两个节点只有一个是空,则错误(不对称)
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isSymmetric = function(root) {
if(root === null) {
return true
}
let l = root.left
let r = root.right
let find = function(left, right) {
if(left === null && right === null) {
return true
} else if(left === null || right === null) {
return false
}
return (left.val === right.val) && find(left.right, right.left) && find(left.left, right.right)
}
return find(l, r)
};
我们再来思考一下迭代的写法,首先递归转迭代一般都需要一个东西存储之前递归的入参,这里我们因为是要从上往下比较,所以是先进先出,很自然地就能想到用队列,然后使用循环并写出条件(如果在递归中中返回true的,这里就应该是continue,毕竟不能只因为一个条件正确就认为这个结果正确,但是false不一样,有一个是错的,结果必定是错的)
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isSymmetric = function(root) {
if(root === null) {
return true
}
let l = root.left
let r = root.right
let queue = [l, r]
while(queue.length !== 0) {
let left = queue.shift()
let right = queue.shift()
if(left === null && right === null) {
continue
} else if(left === null || right === null) {
return false
} else if(left.val !== right.val) {
return false
}
queue.push(left.left)
queue.push(right.right)
queue.push(left.right)
queue.push(right.left)
}
return true
};
10、递归
我再做第9的时候发现自己使用递归还是有点懵逼,这里总结一下套路
首先,递归三部曲:
①找终止条件
②找入参和具体一次的操作
③找返回给上一次递归的值
一、例题
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function(root) {
if(root === null) return 0
let max = 1
let find = function(node, deep) {
if(node === null) {
return
}
max = Math.max(max, deep)
find(node.left, deep + 1)
find(node.right, deep + 1)
}
find(root, max)
return max
};
我们来看一下这道题,首先我们因为看到树其实很自然就能想到要用递归或者迭代(毕竟树可以拆分成多个子树,每个子树做的操作其实都差不多)
然后我们再看一下这道题的三要素:
①终止条件:这道题要求最大深度很显然是要遍历整棵树,而遍历终止的条件就是该节点为空,所以我们的终止条件就找到了,此时的深度就是0
②入参及其操作:我们知道了终止条件,而且也说明了跟每个节点有关,所以我们的入参就是每个节点
每次要做的操作就是上一层的层数+1,就能得到当前的深度
那么这样就有一个问题,我们怎么拿到上一层的深度,很自然地就能想到放到入参里,当然我们也可以想到因为我们有返回值,返回的就是深度,所以直接用返回值+1就ok
所以,最后我们的入参是节点
要做的操作就是深度+1和再次调用函数拿左右节点
③要返回些什么,首先,我们要求的是最大深度,所以我们应该返回的就是当前的深度,然后让上一层通过Math.max来比较即可
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function(root) {
let find = function(node) {
if(node === null) {
return 0
}
let left = find(node.left)
let right = find(node.right)
return Math.max(left, right) + 1
}
return find(root)
};
稍微进阶一下,求N叉树的深度,这个其实就相当于把比较条件变了一下,然后加个循环

var maxDepth = function(root) {
let find = function(node) {
if(node === null) {
return 0
}
let max = 0
for(let item of node.children) {
max = Math.max(max, find(item))
}
return max + 1
}
return find(root)
};
b、两两交换链表中的结点

这一道题我最初是想用快慢指针来做的,结果发现因为是原地交换,有些就会出问题(主要是我菜)
所以这里后来看了下题解,写出了递归的思路
首先,我们依旧来想想为什么要用递归,其实这个分解开来看,就是多个两两交换,而且步骤是重复的,所以很自然能想到递归
然后我们想想什么地方需要递归,什么地方需要我们自己做操作
整个链表可以分为三个部分,目前需要交换的头的部分,交换的后面那个部分,需要递归重复交换的部分
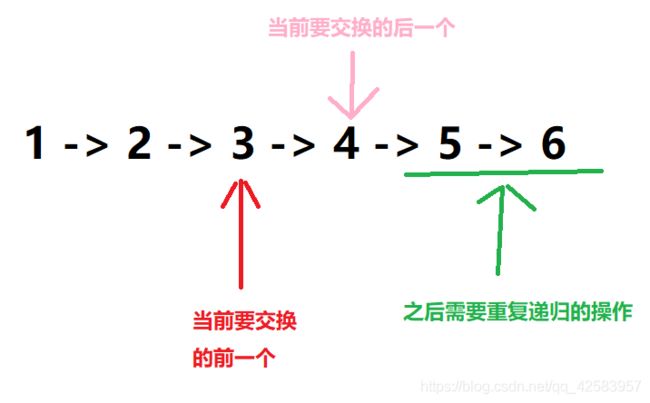
至于为什么没要把之前做过操作的也算进一部分,是因为都已经做过操作了,之后不会做操作,放进来也没啥用
红箭头其实就是我们递归函数的入参,它会不断向后面移动
至于什么时候终止呢?如果红箭头,或者粉箭头为空了,自然就不需要进行递归了
为什么选红箭头和粉箭头为终止条件,而不是用绿箭头呢?因为我们交换的就是红箭头和粉箭头,也就是说递归的终止条件是自己进行操作的部分的条件判断
然后我们再来看一下返回什么,之前有说到入参是不断向后移动的红箭头,那么就相当于是当前的粉色箭头,而因为终止条件也是需要返回值的,那个时候要么自己是空的,要么自己的下一个是空的,所以返回入参(为什么不直接返回null呢,因为我们的入参是红箭头,但我们可能后箭头有值而粉箭头没值)
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var swapPairs = function(head) {
let find = function(head) {
if(head === null || head.next === null) {
return head
}
let next = head.next
head.next = find(next.next)
next.next = head
return next
}
return find(head)
};
c、平衡二叉树

这一道题其实是求二叉树深度的变种,因为我们要判断是否为二叉平衡树,只要左子树是平衡树,右子树也是平衡树且左右子树的深度的绝对值不大于1即可
从这个定义中可以看出,主要要求的是两个东西,所以按常理,我们的返回值也应当是两个(如果只有一个,那么因为是递归,就无法能够进行下一步操作)
然后要明确一点,返回值≠入参,一般情况下二叉树的入参都是节点,可能还会增加些其他的东西,如深度之类的,这里我我们的返回值是{深度,是否为平衡树},那就没必要让入参也是深度了,所以决定入参就是节点
要做的事情其实就一个,判断左右两边是否为平衡树,有一个不是就返回false,并把深度也带上,如果两边深度的绝对值大于1,也返回深度和false,其他情况就说明暂且该子树为平衡树,返回深度和true
这里有一个难点,那就是深度怎么求?
我们要判断是否为平衡树,应当是自底向上的,但我们递归的顺序是自顶向下的,所以肯定会浪费很多空间,但我们求深度,肯定是自底向上的,毕竟我们没办法在根节点就拿到深度,而左右子树的深度又可能是不一样的,所以应当用Math.max来比较一下
但是实际上,这个的求深度就是二叉树求最大深度(见a或如下)
var maxDepth = function(root) {
let find = function(node) {
// 只考虑终止情况下的深度
if(node === null) {
return 0
}
let left = find(node.left)
let right = find(node.right)
return Math.max(left, right) + 1
}
return find(root, 0)
};
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isBalanced = function(root) {
let find = function(node) {
if(node === null) {
return {deep: 0, isBST: true}
}
let left = find(node.left)
let right = find(node.right)
let deep = Math.max(left.deep, right.deep)
if(!left.isBST || !right.isBST) {
return {deep: deep + 1, isBST: false}
}
if(Math.abs(left.deep - right.deep) > 1) {
return {deep: deep + 1, isBST: false}
}
return {deep: deep + 1, isBST: true}
}
return find(root).isBST
};
d、二叉树最小深度
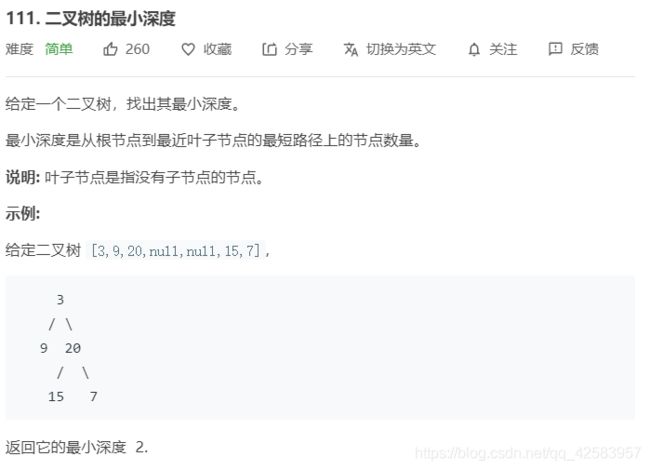
这道题其实有点坑爹,乍一看,感觉就像是求最大深度,但是有个示例[1, 2],却一直过不了,这是因为我们在最大深度时只判断了是否为空,而没有判断过该节点是否为叶子节点(毕竟求最大深度用的是Math.max,只要它的左节点或右节点为null,用max一定能准确找到最大的那个叶子节点)
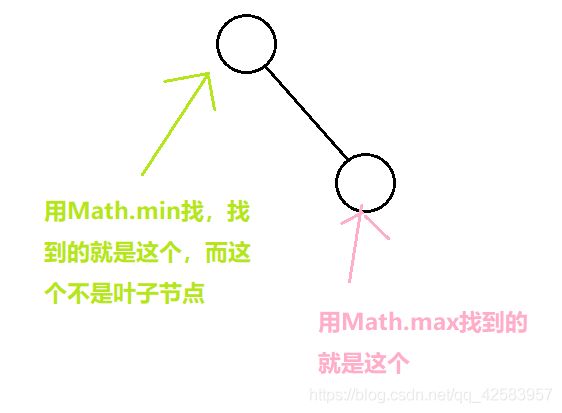
所以要判断,如果左边或者右边没有节点了,那么它的深度应当是左边+右边+1(这里是一个很巧妙的公式,毕竟如果一个个判断是左边为空,所以用右边+1,或者是右边为空,用左边+1,都太麻烦了)
这道题其实主要考察终止条件!!
var minDepth = function(root) {
let find = function(node) {
if(node === null) {
return 0
}
let left = find(node.left)
let right = find(node.right)
if(!node.left || !node.right) {
return left + right + 1
}
return Math.min(left, right) + 1
}
return find(root)
};
e、翻转二叉树
这道题的备注甚骚哈哈哈,这道题就跟镜像差不多,不多讲了,直接上代码
var invertTree = function(root) {
let reverse = function(node) {
if(node === null) {
return node
}
let temp = node.left
node.left = reverse(node.right)
node.right = reverse(temp)
return node
}
return reverse(root)
};
var mergeTrees = function(t1, t2) {
let node = null
let merge = function(left, right, node) {
if(left === null && right === null) {
return null
}
if(node === null) {
node = {left: null, right: null, val: 0}
}
if(left === null) {
node.val = right.val
node.left = merge(null, right.left, node.left)
node.right = merge(null, right.right, node.right)
} else if(right === null) {
node.val = left.val
node.left = merge(left.left, null, node.left)
node.right = merge(left.right, null, node.right)
} else {
node.val = left.val + right.val
node.left = merge(left.left, right.left, node.left)
node.right = merge(left.right, right.right, node.right)
}
return node
}
return merge(t1, t2, node)
};
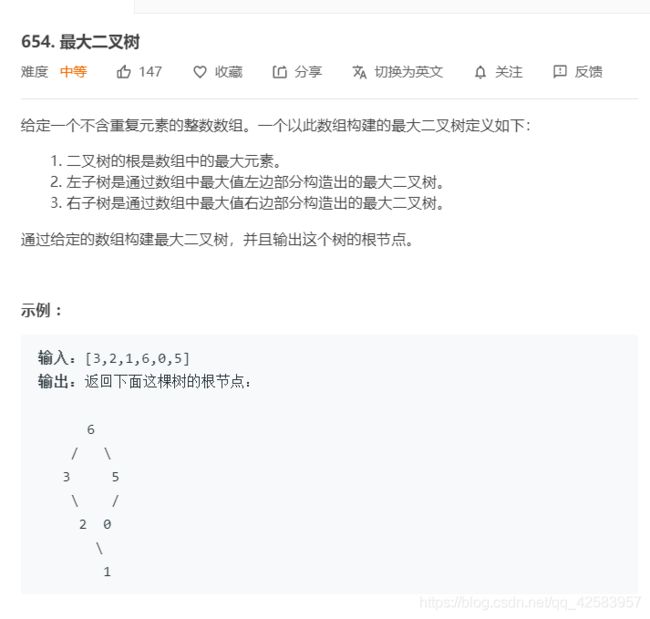
g、最大二叉树
这道题,主要告诉我们其实很多题是真的只能用暴力解法+递归,这已经算是最优解了,所以完全可以先想暴力解法
var constructMaximumBinaryTree = function(nums) {
let find = function(nums) {
if(nums.length === 0) {
return null
}
let node = Math.max(...nums)
let index = nums.indexOf(node)
let treeNode = new TreeNode(node)
treeNode.left = find(nums.slice(0, index))
treeNode.right = find(nums.slice(index + 1))
return treeNode
}
return find(nums)
};
11、逻辑符号
首先两个知识:
|| 短路或,如果 a || b 中 a 是能转化出来等于 true 的就返回 a(短路)
&& 短路与,如果 a && b 中 a 转化出来等于 false,就返回 a(短路)
短路,也就是说不执行后面的,使用 || 或者 && 都是直接输出值而不会转化成boolean类型

所以这道题就有一个很骚的方法,使用短路与,n&&fn(n - 1) + n
如果n === 0那么就不会进行后面的递归了
var sumNums = function(n) {
let res = function(n) {
return n && (n + res(n - 1))
}
return res(n)
};
12、循环遍历
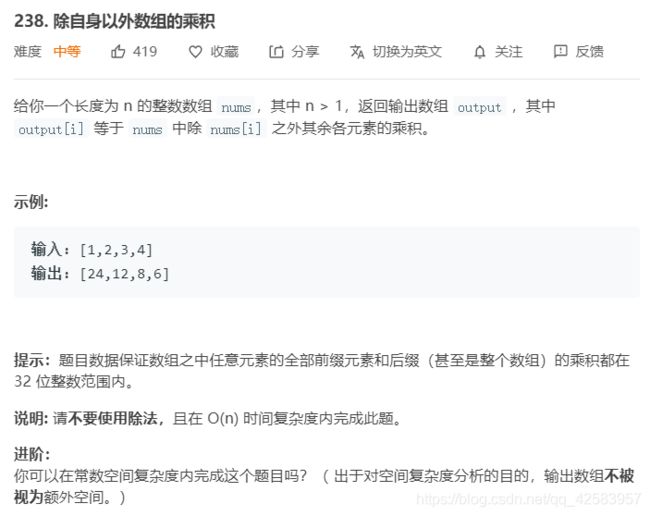
这一道题其实如果不考虑时间复杂度和空间复杂度,可以用出栈入栈的暴力解法来(时间复杂度O(n2))
最简单的方法,就是循环遍历,时间为O(n),用两个常数存储
主要思想就是要求数组乘积,其实就是左边*右边,然后找规律
当然拓宽一下思想就是前缀积 * 后缀积

var productExceptSelf = function(nums) {
let res = []
let left = 1, right = 1
for(let i = 0; i < nums.length; i++) {
res[i] = left
left *= nums[i]
}
for(let i = nums.length - 1; i >= 0; i--) {
res[i] *= right
right *= nums[i]
}
return res
};
13、暴力破解
这里其实就只是想说明一下,不是所有题都有算法的,所以我们很多都只有用暴力破解,如果第一反应没想到简便方法,那么就用暴力破解,管它时间复杂度和空间复杂度之类的
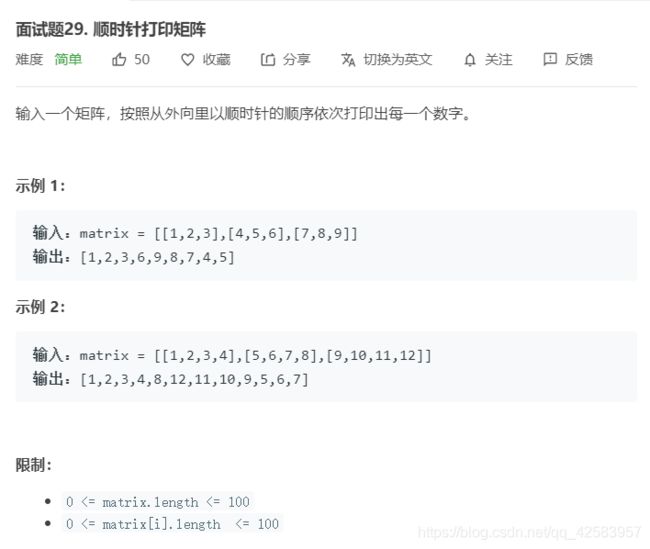
就像这一道题,乍一看,根本看不出什么简便方法(我顶多想到可能用用栈这种东西),所以就直接暴力破呗,不要怕
var spiralOrder = function(matrix) {
let res = []
while(matrix.length !== 0) {
let top = matrix.shift()
res.push(...top)
for(let i = 0; i < matrix.length - 1; i++) {
if(matrix[i].length === 0) break
let value = matrix[i].pop()
res.push(value)
}
if(matrix.length >= 1) {
let bottom = matrix.pop().reverse()
res.push(...bottom)
}
for(let i = matrix.length - 1; i >= 0; i--) {
if(matrix[i].length === 0) break
let value = matrix[i].shift()
res.push(value)
}
}
return res
};
14、看着很吓人的题
a、翻转字符串

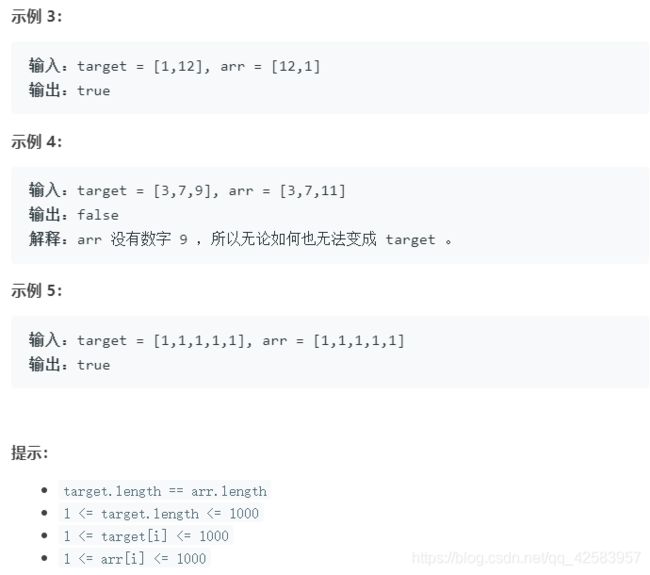
之前做题从来没有关注过提示,这次我们从提示入手,首先,提示说最多有1000个数,意思就是时间复杂度可以为O(n2),然后我们再来思考一下这道题,这道题,初看确实没啥想法,但一想暴力解法肯定不在这个时间复杂度里吧,排除暴力解法,我们再想想
题中有提到,可能会有两个相邻元素交换顺序,或是多个元素倒序,可能看多个元素看不出什么东西来,但是相邻元素交换顺序不就是冒泡吗??所以我们就试试将两个数组都先排序,然后再比较,一看结果,正确的,这就证明了排序可行
var canBeEqual = function(target, arr) {
target = target.sort()
arr = arr.sort()
for(let i = 0; i < target.length; i++) {
if(target[i] !== arr[i]) {
return false
}
}
return true
};
b、检查字符串是否包含所有长度为K的二进制子串

首先理解下题意,题意用白话来说就是,通过k来构造k位数的01这种字符串,然后去s中找,但是如果先把所有字符串找到,然后在s中循环找就很麻烦,所以直接通过在s中查找所有类型的字符串,然后看总个数是否大于等于2**k即可
var hasAllCodes = function(s, k) {
let set = new Set()
for(let i = 0; i < s.length; i++) {
if(i + k <= s.length) {
set.add(s.slice(i, i + k))
} else {
break
}
}
return set.size >= 2 ** k
};
c、三数之和
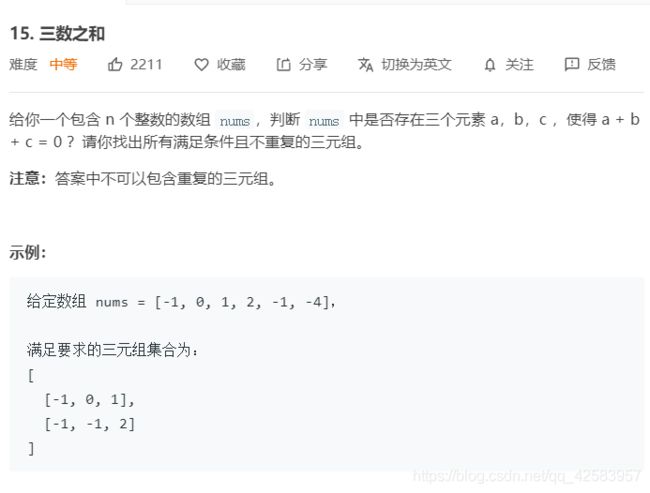
做这道题的时候隐隐约约觉着要用排序+双指针,但是具体怎么搞却没有思路。但是其实这就是一个快排类型的题,难点其实在于不能重复,这个问题,不多说,直接上代码
var threeSum = function(nums) {
nums = nums.sort(function(a, b) {
return a - b
})
let res = []
for(let i = 0; i < nums.length; i++) {
if(nums[i] > 0) {
return res
}
// 去重
if(i >= 1 && nums[i] === nums[i - 1]) {
continue
}
let left = i + 1
let right = nums.length - 1
while(left < right) {
if(nums[left] + nums[right] + nums[i] < 0) {
left++
} else if(nums[left] + nums[right] + nums[i] === 0) {
res.push([nums[i], nums[left], nums[right]])
// 去重
while(left < right && nums[left] === nums[left + 1]) {
left++
}
// 去重
while(left < right && nums[right] === nums[right - 1]) {
right--
}
left++
right--
} else {
right--
}
}
}
return res
};
d、转变数组后最接近目标值的数组和
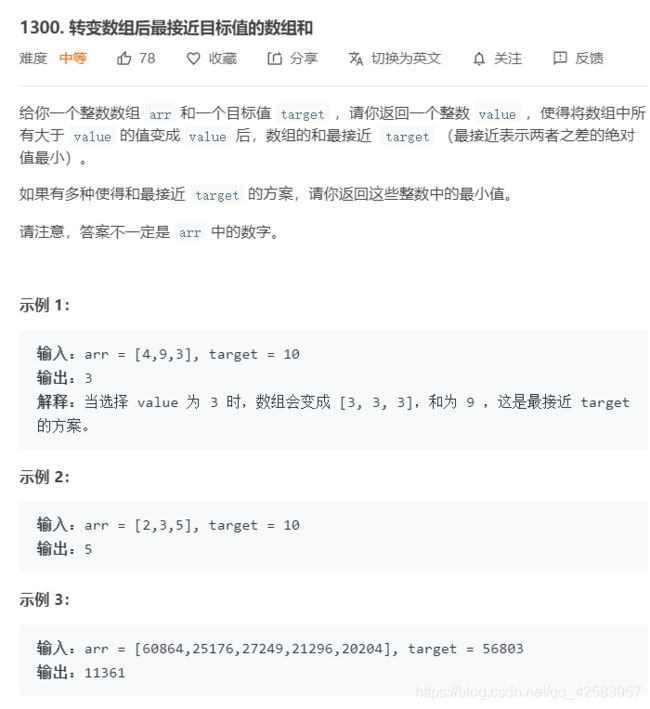
这道题我已经算是很接近答案了,只不过有两个问题,而最终没有解决主要是两个问题没弄清楚,第一个是数组和最接近这个的意思就是要比较Math.floor()和Math.ceil()哪个值更接近平均值,第二个是每次循环都要去找剩下数组的平均值,而不是先判断target和当前的arr[i]的大小后再去找平均值
想清楚这两点,其实这道题就很简单
/**
* @param {number[]} arr
* @param {number} target
* @return {number}
*/
var findBestValue = function(arr, target) {
arr = arr.sort((a, b) => a - b)
let res = arr[0]
for(let i = 0; i < arr.length; i++) {
let avg = target / (arr.length - i)
let value = Math.floor(avg)
if(Math.abs(avg - Math.ceil(avg)) < Math.abs(avg - value)) {
value = Math.ceil(avg)
}
if(value > arr[i]) {
target -= arr[i]
res = arr[i]
} else {
if(target === arr[i]) {
return arr[i]
} else {
return value
}
}
}
return res
};
e、课程安排 IV


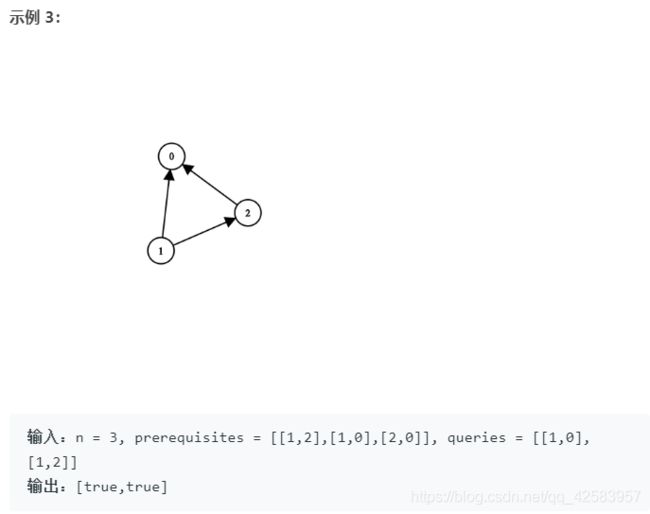

这道题其实只要别被这么多字难住,然后把某一门课和能达到的课用一个map来存储,里面的key就是那门先修课,value就是能到达的所有课,这样就能判断了
/**
* @param {number} n
* @param {number[][]} prerequisites
* @param {number[][]} queries
* @return {boolean[]}
*/
var checkIfPrerequisite = function(n, prerequisites, queries) {
let map = {}
let res = []
// 构建图
for(let item of prerequisites) {
if(!map[item[0]]) {
map[item[0]] = new Set()
}
map[item[0]].add(item[1])
}
for(let key in map) {
map[key].forEach(value => {
if(map[value]) {
console.log(key,value, ...map[value],map[key])
for(let item of map[value]) {
map[key].add(item)
}
}
})
}
for(let item of queries) {
res.push(map[item[0]] ? map[item[0]].has(item[1]) : false)
}
return res
};
f、摘樱桃II

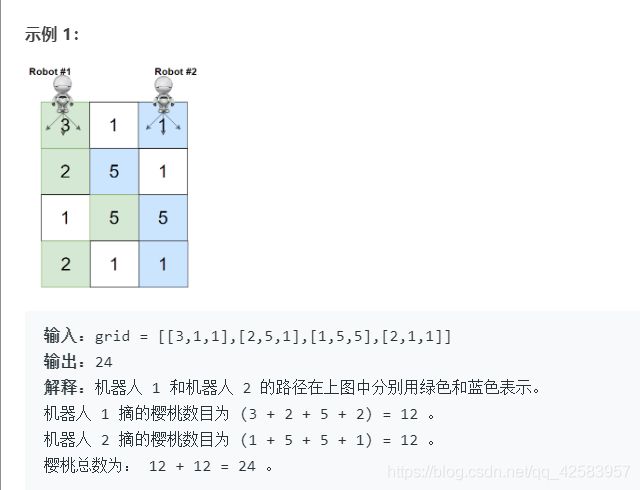

这道题其实从动态规划的角度上不难,只要想到了动态规划就可以,难的是条件的判断,以及最开始所有的初始值为-1这一个点,我之前使用0,但是因为0会出现在grid数组里,所以一直报错,最后才发现是初始值的问题
/**
* @param {number[][]} grid
* @return {number}
*/
var cherryPickup = function(grid) {
let dp = new Array(grid.length)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(grid[0].length)
for(let j = 0; j < grid[0].length; j++) {
// 设置为-1是重点
dp[i][j] = new Array(grid[0].length).fill(-1)
}
}
// dp[i][j][k]表示当走到第i行,第一个机器人在j,第二个机器人在k的时候最大的樱桃数目
// 初始化第一行,第一行只有可能是dp[0][0][dp[0].length - 1] = grid[0][0] + grid[0][dp[0].length - 1]
dp[0][0][dp[0].length - 1] = grid[0][0] + grid[0][dp[0].length - 1]
let res = 0
for(let i = 1; i < grid.length; i++) {
for(let j = 0; j < dp[0].length; j++) {
for(let k = j + 1; k < dp[0].length; k++) {
// 循环找上一层最大的(从左上,上,右上角三个地方中选最大)
for(let m = j - 1; m < j + 2; m++) {
if(m < 0) {
continue
}
for(let n = k - 1; n < k + 2; n++) {
if(n >= dp[0].length) {
break
}
// 判断值为-1是重点(这代表着这一步不能走)
if(m >= n || dp[i - 1][m][n] === -1 ) {
continue
}
// 直接比较dp[i][j][k]是重点
dp[i][j][k] = Math.max(dp[i][j][k], dp[i - 1][m][n] + grid[i][j] + grid[i][k])
}
}
res = Math.max(res, dp[i][j][k])
}
}
}
return res
};
g、进制转换
转36进制
function change(num) {
let res = ''
do {
let value = num % 36
num = (num - value) / 36
if(value >= 10) {
value = String.fromCharCode('a'.charCodeAt() + value - 10)
}
res = value + res
} while(num !== 0)
return res
}
十进制转换其他进制模板(转更高进制的,低进制就少个判断):
// bit代表需要转换的进制
function change(num, bit) {
let res = ''
do{
let value = num % bit
num = (num - value) % bit
// 这是针对高进制,低进制不需要,毕竟不会有字母
if(value >= 10) {
value = String.fromCharCode('a'.charCodeAt() + value - 10)
}
// 重点,先得到的会放后面
res = value + res
} while (num !== 0)
return res
}
重点,一个是什么时候用/,什么时候用%,String.fromCharCode(xx)将xx返回成utf-16编码,String.prototype.charCodeAt()将字符串转成UTF-16编码
h、从先序遍历还原二叉树
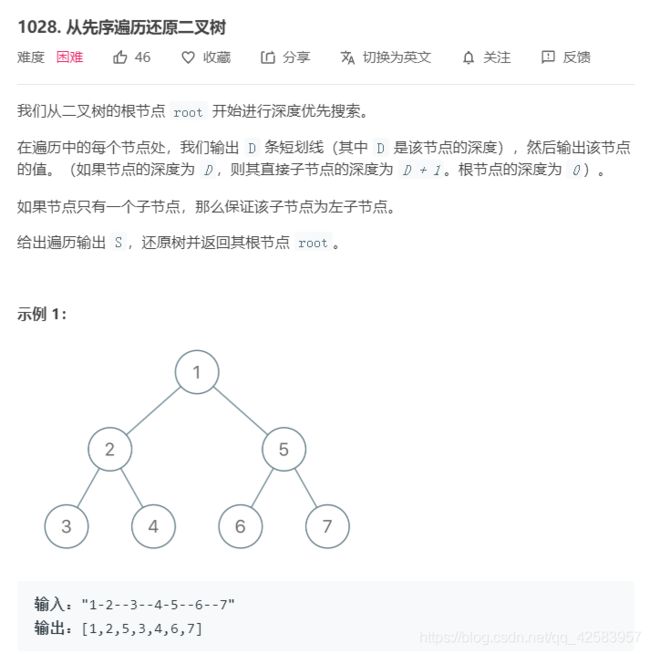
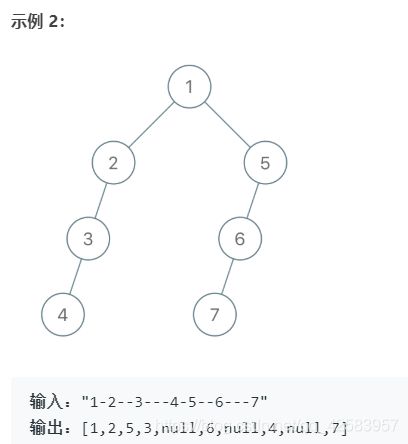
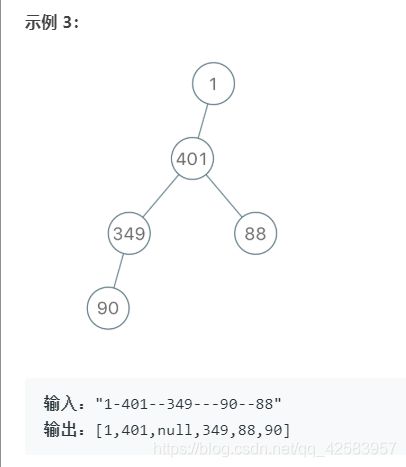
这道题首先因为是先序遍历,所以是根节点 -> 左孩子 -> 右孩子
这其实就是个找父亲的过程,使用深度的单调递增栈,如果孩子深度(即-个数)>栈顶,就入栈,否则出栈,一直循环到找到父亲
/**
* @param {string} S
* @return {TreeNode}
*/
var recoverFromPreorder = function(S) {
let root = new TreeNode(S.match(/(\d+)/)[0])
let arr = S.match(/(-+)(\d+)/g)
if(arr === null) return root
let stack = [root]
let deep = [-1]
for(let i = 0; i < arr.length; i++) {
while(arr[i].lastIndexOf('-') <= deep[deep.length - 1]) {
deep.pop()
stack.pop()
}
let node = new TreeNode(parseInt(arr[i].replace(/-/g, '')))
// 先构造树,再入栈(所有都要入栈)
if(stack[stack.length - 1].left) {
stack[stack.length - 1].right = node
} else {
stack[stack.length - 1].left = node
}
stack.push(node)
deep.push(arr[i].lastIndexOf('-'))
}
return root
};
i
/**
* @param {number} n
* @param {number[][]} connections
* @return {number}
*/
var minReorder = function(n, connections) {
connections = connections.sort((a, b) => Math.min(a[0], a[1]) - Math.min(b[0], b[1]))
console.log(connections)
let city = new Set()
city.add(0)
let res = 0
for(let i = 0; i < connections.length; i++) {
if(city.has(connections[i][1])) {
city.add(connections[i][0])
} else if(city.has(connections[i][0])){
res++
city.add(connections[i][1])
}
}
return res
};
i、重新规划路线
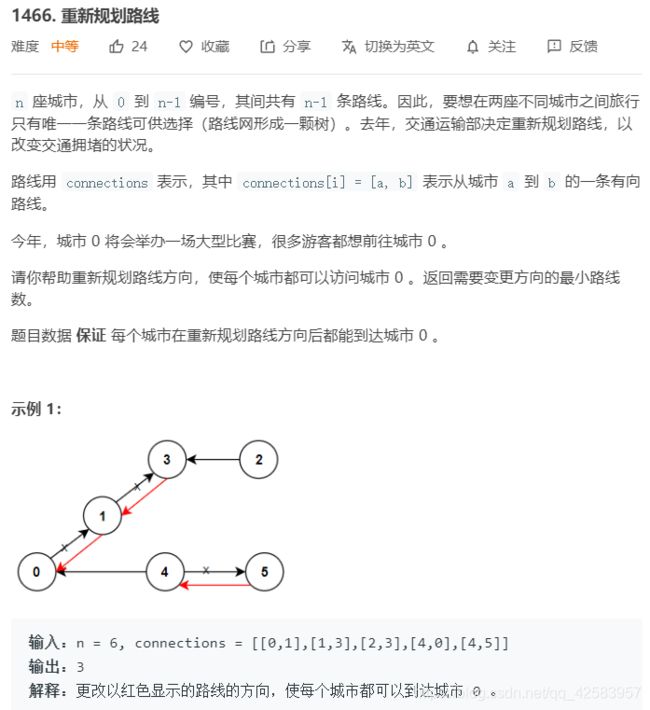

这道题的正规做法应该是使用图的DFS或者BFS,奈何我不会(之后补),所以这里采用了维持一个数组,遍历各路径(这里遍历的路径里存在的点要先排序,毕竟遍历的时候是连续的,所以应该先对所有路径排序,保证后面出现的点一定是比前面出现的点大的)

/**
* @param {number} n
* @param {number[][]} connections
* @return {number}
*/
var minReorder = function(n, connections) {
connections = connections.sort((a, b) => Math.min(a[0], a[1]) - Math.min(b[0], b[1]))
console.log(connections)
let city = new Set()
city.add(0)
let res = 0
for(let i = 0; i < connections.length; i++) {
if(city.has(connections[i][1])) {
city.add(connections[i][0])
} else if(city.has(connections[i][0])){
res++
city.add(connections[i][1])
}
}
return res
};
DFS和邻接链表的写法
这里要明确,因为DFS是自顶向下(其实BFS也是自顶向下),所以如果发现能从start到end,就说明要重新规划了
而因为这里最开始是有向图,为了知道什么是能到的,什么是不能到的,就把它弄成无向图,但是要设置一下什么是自己添加的(如果不做成无向图就没办法让这棵树连通,就更没办法往下遍历了)
然后因为图有两条边,但是不能经过同一顶点两次,所以拿个数组存一下,然后再用栈存一下顶点
var minReorder = function(n, connections) {
let map = new Array(n)
// 打个比方 [[[1, 1], [2, 1]], [[2, 1]]]
// 这个的意思是0能到1,也能到2
// 1能到2
for(let [start, end] of connections) {
if(!map[start]) {
map[start] = []
}
// 存1是有讲究的,因为是DFS,自顶向下,所以如果能找到start对应的end就说明是要重新规划的,存1方便到时候加
map[start].push([end, 1])
// end -> start 是人为手动添加的,这样就是无向图了
if(!map[end]) {
map[end] = []
}
// 因为如果没出现start->end就一定是end->start,如果遍历到了,因为是自底向上,所以不用重新规划
map[end].push([start, 0])
}
// 保存经过了的节点
let visited = new Array(n).fill(false)
let queue = [0]
let res = 0
while(queue.length !== 0) {
let start = queue.shift()
visited[start] = true
for(let [city, flag] of map[start]) {
// 如果已经走过该节点,就继续循环
if(visited[city]) {
continue
}
res += flag
queue.push(city)
}
}
return res
};
j、最接近的三数之和

这一道题和之前的15题差不多也是三数之和,也是使用排序+双指针
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var threeSumClosest = function(nums, target) {
nums = nums.sort((a, b) => a - b)
let sum = nums[0] + nums[1] + nums[2]
for(let i = 0; i < nums.length; i++) {
let left = i + 1, right = nums.length - 1
while(left < right) {
let val = nums[i] + nums[left] + nums[right]
if(Math.abs(target - val) < Math.abs(target - sum)) {
sum = val
}
if(val === target) {
return target
} else if(val > target) {
right--
} else {
left++
}
}
}
return sum
};
k、单词拆分

字符串!!,动态规划!!!,跟回文数其实差不多,知道动态规划后基本上5分钟搞定,虽然我这没想出来是动态规划
/**
* @param {string} s
* @param {string[]} wordDict
* @return {boolean}
*/
var wordBreak = function(s, wordDict) {
let dp = new Array(s.length + 1).fill(false)
dp[0] = true
for(let i = 1; i < dp.length; i++) {
for(let item of wordDict) {
if(dp[i]) {
break
}
if(item.length > i) {
continue
} else {
dp[i] = dp[i - item.length] && (s.substring(i - item.length, i) === item)
}
}
}
return dp[s.length]
};
/**
* @param {ListNode} head
* @return {ListNode}
*/
var removeDuplicateNodes = function(head) {
let set = new Set()
let node = head
while(node !== null && node.next !== null) {
set.add(node.val)
let next = node.next
if(set.has(next.val)) {
while(next !== null && set.has(next.val)) {
next = next.next
}
node.next = next
}
node = node.next
}
return head
};
m、缺失的第一个正数

1、暴力解法
这个解法是很容易就能想到的,主要就是考虑情况(面向测试用例编程),过滤的时间复杂度是O(N),里面找最小也是O(N),空间复杂度就是O(1)
/**
* @param {number[]} nums
* @return {number}
*/
var firstMissingPositive = function(nums) {
nums = nums.filter(item => item > 0)
if(nums.length === 0) {
return 1
}
let min = Math.min(...nums)
let max = Math.max(...nums)
if(min - 1 > 0) {
return 1
} else {
let result = Number.MAX_VALUE
for(let item of nums) {
if(item - 1 > 0 && nums.indexOf(item - 1) === -1) {
result = Math.min(item - 1, result)
} else if(nums.indexOf(item + 1) === -1) {
result = Math.min(item + 1, result)
}
}
if(result === Number.MAX_VALUE) {
return max + 1
} else {
return result
}
}
};
2、原地哈希
这个其实我也想到了,就是结合下标和值,但不知道咋的就以为时间复杂度是O(n2),但实际上如果放对位置或者是负数或0,就不会移动位置,所以是O(n2)
而且我们要求出的最小正数是[1, len + 1]里的
/**
* @param {number[]} nums
* @return {number}
*/
var firstMissingPositive = function(nums) {
let swap = function(nums, i, j) {
let temp = nums[i]
nums[i] = nums[j]
nums[j] = temp
}
for(let i = 0; i < nums.length; i++) {
// nums[i]是可以与nums.length相等的
while(nums[i] > 0 && nums[i] <= nums.length && nums[nums[i] - 1] !== nums[i]) {
swap(nums, nums[i] - 1, i)
}
}
for(let i = 0; i < nums.length; i++) {
if(nums[i] - 1 !== i) {
return i + 1
}
}
return nums.length + 1
};
/**
* @param {number} s
* @param {number[]} nums
* @return {number}
*/
var minSubArrayLen = function(s, nums) {
let left = 0, right = 0
let sum = 0
let count = Number.MAX_VALUE
while(right < nums.length) {
if(nums[right] >= s) {
return 1
}
sum += nums[right]
right++
while(sum >= s) {
count = Math.min(count, right - left)
sum -= nums[left]
left++
}
}
return count === Number.MAX_VALUE ? 0 : count
};
/**
* @param {number} shorter
* @param {number} longer
* @param {number} k
* @return {number[]}
*/
var divingBoard = function(shorter, longer, k) {
if(k === 0) {
return []
}
let arr = []
for(let i = 0; i <= k; i++) {
arr.push(shorter * i + longer * (k - i))
}
arr = arr.sort((a, b) => a - b)
return Array.from(new Set(arr))
};
14、难题,不是很懂
a、正则表达式匹配

先明确一下,单独的一个.是可以存在的,不依靠其他的进行判断
但是*要么与前面的某一位一起跟某几个相同的字符匹配,要么跟某一个相同的字符匹配,要么跟后面的空气进行匹配
否则就不匹配
不匹配和跟跟空气匹配其实结果是一样的,但是我们这里分的条件是匹配和不匹配,所以要分开写
因为*依靠前一位,所以初始化的时候就应该让是*的那个结果和倒数第二位的相同
/**
* @param {string} s
* @param {string} p
* @return {boolean}
*/
var isMatch = function(s, p) {
let dp = new Array(s.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(p.length + 1).fill(false)
}
dp[0][0] = true
// 这个初始化相当重点
for(let j = 1; j < dp[0].length; j++) {
if(p[j - 1] === '*') {
console.log(dp[0][j - 2])
dp[0][j] = dp[0][j - 2]
}
}
for(let i = 1; i < dp.length; i++) {
for(let j = 1; j < dp[0].length; j++) {
// 如果上一位是.,或者这一位能匹配上
// 那么结果就跟上一次的相同
if(s[i - 1] === p[j - 1] || p[j - 1] === '.') {
dp[i][j] = dp[i - 1][j - 1]
// 否则如果是*就再继续分
// 如果是其他乱七糟八的还匹配不上,铁定就是false(也就是初始值)
} else if(p[j - 1] === '*'){
// *因为不能单独出现,必须和其他字母一起搭配
// 所以分两种情况
// 这里不匹配的情况
if(s[i - 1] !== p[j - 2] && p[j - 2] !== '.') {
dp[i][j] = dp[i][j - 2]
} else {
// 这里是匹配的情况
// 所以这里分3种情况,以下任意一种成立就可以
// 1、只匹配得上一个,dp[i][j - 1]
// 2、匹配空气,dp[i][j - 2]
// 3、能匹配多个,就说明s少一位p也能匹配上,dp[i - 1][j]
dp[i][j] = dp[i][j - 1] || dp[i][j - 2] || dp[i - 1][j];
}
}
}
}
return dp[s.length][p.length]
};
/**
* @param {string} s
* @param {string} p
* @return {boolean}
*/
var isMatch = function(s, p) {
let dp = new Array(s.length + 1)
for(let i = 0; i < dp.length; i++) {
dp[i] = new Array(p.length + 1).fill(false)
}
dp[0][0] = true
for(let j = 1; j < dp[0].length; j++) {
if(p[j - 1] === '*') {
dp[0][j] = dp[0][j - 1]
}
}
for(let i = 1; i < dp.length; i++) {
for(let j = 1; j < dp[0].length; j++) {
if(p[j - 1] === s[i - 1] || p[j - 1] === '?') {
dp[i][j] = dp[i - 1][j - 1]
} else if(p[j - 1] === '*') {
dp[i][j] = dp[i - 1][j] || dp[i][j - 1]
}
}
}
return dp[s.length][p.length]
};
b、二叉树的最大路径和

这道题其实说难也不难,主要就是看到二叉想遍历,最开始我是在纠结使用中序还是后序(毕竟根节点可能不要,如果用先序就会直接放进去),但其实这道题用递归是最方便的(迭代还太麻烦,我也想不出方法)
这道题总共就四种情况
以这三个节点为例,就可能是A,AB,AC,ABC
而这里面AB和AC可以合并,因为我们必然会去分开求B、C各自的最大值(毕竟还有ABC)
而且这里很明显可以看出,无论如何A的值都是需要的,然后我们就可以开始递归了(需要递归的点其实就是B和C,因为B和C可以继续往下分,而且B和C可以通过A的left和A的right得到)
/**
* @param {TreeNode} root
* @return {number}
*/
var maxPathSum = function(root) {
// 因为必须包含一个节点,所以初始化的值是根节点的值而不是0
let max = root.val
let getSum = function(root) {
if(root === null) {
return 0
}
// 这里其实分三种情况,只需要左边,只需要右边,左右都要
// 用左边和0比较,如果0大就说明不要左边
let left = Math.max(0, getSum(root.left))
// 用右边和0比较,如果0大就说明不要右边
let right = Math.max(0, getSum(root.right))
// 用最大值和左右都要比较
// 因为至少包含一个节点,那么这个节点一定是我每次遍历到的那个节点
max = Math.max(max, root.val + left + right)
// 返回的就是左边或者右边中的最大值
return root.val + Math.max(left, right)
}
getSum(root, max)
return max
};
c、二叉搜索树的后序遍历

这道题解法其实用的就是之前的那道h、二叉树的先序遍历里的单调栈
这里说明一下,为什么要用单调栈,二叉搜索树是一种很明显的有序的东西,单调栈里最主要的就是单调俩字,所以单调栈天生跟排序就很有关系
这道题其实也是找父亲,因为最开始我们假设了一个无穷大的根节点,所以来的节点一定是左边的,比这个小的
/**
* @param {number[]} postorder
* @return {boolean}
*/
var verifyPostorder = function(postorder) {
// 单调栈
let stack = []
// 原本顺序是left -> right -> root
// 倒序一下就是root -> right -> left
// 就有点像先序遍历的镜像,因为先序遍历是root -> left -> right
// 相当于给树再加一个父亲,现在的树时无穷大的数的左子树
// 记录下上一个父亲的结果
let pre = Number.MAX_VALUE
for(let i = postorder.length - 1; i >= 0; i--) {
// 因为顺序是root -> right -> left
// right > root,所以只要postorder[i] >= pre就说明不是二叉搜索树
if(pre <= postorder[i]) {
return false
}
// 如果小于栈顶元素,说明右边没东西了,就是往左子树里加东西
while(stack.length !== 0 && postorder[i] < stack[stack.length - 1]) {
// 所以把右边的都从stack里去掉
pre = stack.pop()
}
stack.push(postorder[i])
}
return true
};
d、模式匹配

这道题就一道二元一次方程,通过暴力破就行,难点其实在于找边界,就面向测试用例
/**
* @param {string} pattern
* @param {string} value
* @return {boolean}
*/
var patternMatching = function(pattern, value) {
// 其实这道题就是二元一次方程
// a的个数 * 代表a的字母长度 + b的个数 * 代表b的字母长度 = value.length
// 我们假设a的字母长度(通过遍历)
// 然后通过计算求出b的字母长度 = (value.length - a的个数 * 代表a的字母长度) / b的个数
// 然后再把它拼起来与原pattern比较即可
if(pattern.length === 0 && value.length === 0) {
return true
}
if(pattern.length === 0) {
return false
}
// flag来表示开头第一个是否为a
let a = 0, b = 0, flag = true
for(let i = 0; i < pattern.length; i++) {
if(i === 0 && pattern[i] === 'b') {
flag = false
}
if(pattern[i] === 'a') {
a++
} else {
b++
}
}
// 如果在value为空的情况下,a和b同时存在,又因为a的字符不能等于b的字符
if(value.length === 0 && a && b) {
return false
}
// 如果只有a,或者只有b
if(b === 0) {
let lenA = value.length / a
if((lenA).toString().indexOf('.') !== -1) {
return false
}
let aChar = value.substring(0, lenA)
return aChar.repeat(a) === value
}
if(a === 0) {
let lenB = value.length / b
if((lenB).toString().indexOf('.') !== -1) {
return false
}
let bChar = value.substring(0, lenB)
return bChar.repeat(b) === value
}
if(!flag) {
let temp = a
a = b
b = temp
pattern = pattern.replace(/a/g, 'c')
pattern = pattern.replace(/b/g, 'a')
pattern = pattern.replace(/c/g, 'b')
}
let lenA = 0
let lenB = 0
// 遍历a的字母长度
// a可以为空,a也可以为满
// b的字母长度 = (value.length - a的个数 * 代表a的字母长度) / b的个数
for(let i = 0; i <= value.length; i++) {
lenA = i
lenB = (value.length - a * lenA) / b
if((lenB).toString().indexOf('.') !== -1) {
continue
}
let str = ''
let nowIndex = 0
let aChar = value.substring(nowIndex, nowIndex + lenA)
let bChar = ''
for(let j = 0; j < pattern.length; j++) {
if(pattern[j] === 'a') {
str += aChar
if(bChar === '') {
nowIndex = nowIndex + lenA
}
} else {
if(bChar === '') {
bChar = value.substring(nowIndex, nowIndex + lenB)
}
str += bChar
}
}
if(str === value) {
return true
}
}
return false
};