算法与数据结构学习之路三:算法与数据结构的融合应用 -- 数组问题
文章目录
- 一、数组
- 1. 杨辉三角问题
- 2. 最大子序列和问题
- 3. 双指针问题
- 4. Majority Element问题(数组中出现次数最多的元素)
- 5. 抽屉(鸽巢)/一个萝卜一个坑问题
- 6. 动态规划问题
- 6.1 斐波那契数列
- 6.2 背包问题
- 6.3 其他动态规划问题
- 7. 滑动窗口方法
- 8. 散列集合问题
- 9. 排序问题
一、数组
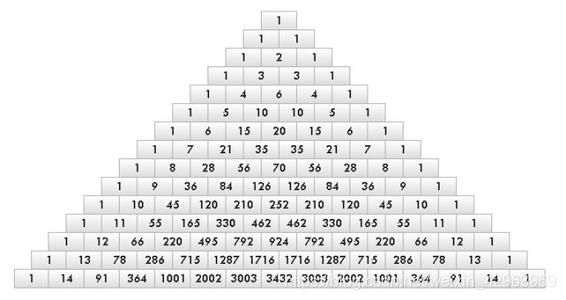
1. 杨辉三角问题
杨辉三角,是二项式系数在三角形中的一种几何排列。
杨辉三角的重要数学性质:(1). 每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和,这也是组合数的性质之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。
(2). 第n行的m个数可表示为 C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。
杨辉三角问题:
①. 118.杨辉三角-------------------------------------------------------------------------------------------------------------------------------------------------------------
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
| 输入 | 输出 |
|---|---|
| 5 | [ [1],[1,1],[1,2,1],[1,3,3,1], [1,4,6,4,1]] |
class Solution {
public:
vector> generate(int numRows) {
vector>ans(numRows);
if(numRows==0)
return ans;
for(int i=0;i ②. 119. 杨辉三角 II (动态规划问题)--------------------------------------------------------------------------------------------------------------------------------------
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
| 输入 | 输出 |
|---|---|
| 3 | [1,3,3,1]] |
利用动态规划,设两个长度为k+1,初始化为1的数组,分别用于存放第i行和第i-1行的数字,将计算的i+1行数字覆盖第i-1行
class Solution {
public:
vector getRow(int rowIndex) {
vector res(rowIndex+1,1); //用于存放第i行数组
vector temp(rowIndex+1,1); //用于存放第i-1行数组
for(int i=2;i<=rowIndex;i++){
for(int j=1;j<=i-1;j++){
res[j]=temp[j-1]+temp[j]; //根据杨辉三角的性质,第i行等于第i-1行的两个数相加
}
temp=res;
}
return res;
}
};
2. 最大子序列和问题
最大子序列和问题是最常见的一类问题。
最大子序列和问题
①. 53.最大子序列和(这个问题没有限制子序列的长度)--------------------------------------------------------------------------------------------------------
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
| 输入 | 输出 | 解释 |
|---|---|---|
| [-2,1,-3,4,-1,2,1,-5,4], | 6 | 连续子数组 [4,-1,2,1] 的和最大,为 6。 |
(1).贪心算法(贪婪算法)求解:
贪心算法(策略)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,它所做出的仅仅是在某种意义上的局部最优解。选择的贪心策略必须具备无后效性(即某个状态以后的过程不会影响以前的状态,只与当前状态有关)
class Solution {
public:
int maxSubArray(vector& nums) {
int sum=0;
int ans=-INT_MAX; //ans需要设置到最小整数,否则当子序列和为负数时结果为0;
for(int i=0;i0时,累加计算
ans=max(sum,ans); //通过求解最大值,获取最终的最大的子列和,这时是一个局部解
}
return ans;
}
};
(2).分治算法求解:
②. 121. 买卖股票的最佳时机---------------------------------------------------------------------------------------------------------------------------------------------
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。
| 输入 | 输出 | 解释 |
|---|---|---|
| [7,1,5,3,6,4] | 5 | 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。 |
思路:此问题也是最大子序列和的一个变种问题,面对股票价格的变化,我们可以两两之间作差,这样价格就变成了收益,要求最大收益就是求收益的最大子序列和。
class Solution {
public:
int maxProfit(vector& prices) {
vector diff;
for(int i=1;i 3. 双指针问题
双指针问题,顾名思义就是在数组中设立两个指针。双指针分为同向双指针和相向双指针。
相向双指针是在算法的一开始,两根指针分别位于数组/字符串的两端,并相向行走。
同向双指针是算法的一开始,两根指针分别位于数组/字符串的一段,同向行走。
双指针问题
①. 27. 移除元素(同向双指针)-----------------------------------------------------------------------------------------------------------------------------------------------
给定一个数组 nums 和一个值 val,你需要原地移除所有数值等于 val 的元素,返回移除后数组的新长度。不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
| 输入 | 输出 | 解释 |
|---|---|---|
| nums = [3,2,2,3], val = 3 | 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 | 你不需要考虑数组中超出新长度后面的元素。 |
思路:设置两个同向双指针,其中i是慢指针,j是快指针,i指针指向匹配元素的索引,j指针跳过匹配元素。
class Solution {
public:
int removeElement(vector& nums, int val) {
int i=0;
for(int j=0;j ②. 88. 合并两个有序数组(倒序同向双指针)-----------------------------------------------------------------------------------------------------------------------------
给定两个有序整数数组 nums1 和 nums2,将 nums2 合并到 nums1 中,使得 num1 成为一个有序数组。
说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n。你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n)来保存 nums2 中的元素。
| 输入 | 输出 | 解释 |
|---|---|---|
| nums1 = [1,2,3,0,0,0], m = 3 nums2 = [2,5,6], n = 3 |
[1,2,2,3,5,6] |
思路:因为题目是有序数组,且组合后的数组长度count=m+n-1,由于组合后的数据仍为有序数据,所以可以从组合后的最后一个元素开始,比较两个有序数组的最后元素的大小,大的放到最后。
void merge(vector& nums1, int m, vector& nums2, int n) {
int second=n-1;
int first=m-1;
int count=m+n-1;
while(second>=0 && first>=0){ //双指针,从后开始比较,数据大的放到最后。
nums1[count--] = nums1[first] >nums2[second] ?nums1[first--]:nums2[second--];
}
while(second>=0) //剩下的复制到nums中
nums1[count--]=nums2[second--];
}
③. 283. 移动零(同向双指针)-----------------------------------------------------------------------------------------------------------------------------------------------
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
| 输入 | 输出 | 解释 |
|---|---|---|
| [0,1,0,3,12] | [1,3,12,0,0] | 必须在原数组上操作,不能拷贝额外的数组。 |
思路:题目中只移动0,可以设置同向的两个指针,一个指针指向0元素的索引,另一个指针遍历数组。
class Solution {
public:
void moveZeroes(vector& nums) {
if(nums.size()<=1)
return;
int i=0; //i指针指向0元素的索引
for(int j=0;j ④. 888. 公平的糖果交换(同向双指针)-----------------------------------------------------------------------------------------------------------------------------------
爱丽丝和鲍勃有不同大小的糖果棒:A[i] 是爱丽丝拥有的第 i 块糖的大小,B[j] 是鲍勃拥有的第 j 块糖的大小。因为他们是朋友,所以他们想交换一个糖果棒,这样交换后,他们都有相同的糖果总量。(一个人拥有的糖果总量是他们拥有的糖果棒大小的总和。)返回一个整数数组 ans,其中 ans[0] 是爱丽丝必须交换的糖果棒的大小,ans[1] 是 Bob 必须交换的糖果棒的大小。
| 输入 | 输出 | 解释 |
|---|---|---|
| A = [1,1], B = [2,2] | [1,2] | |
| A = [1,2], B = [2,3] | [1,2] | |
| A = [2], B = [1,3] | [2,3] |
思路:仔细分析问题,设爱丽丝的糖果的总数为A,鲍勃的糖果的总数为B,要交换糖果使两人糖果相同,则有公式 A − x + y = B + x − y A-x+y=B+x-y A−x+y=B+x−y 整理后可以得到:
y = x − ( A − B ) / 2 y=x-(A-B)/2 y=x−(A−B)/2
所以,对爱丽丝中每个不重复的元素x,在鲍勃中都有一个y对应上述的公式。所以程序如下所示:
class Solution {
public:
vector fairCandySwap(vector& A, vector& B) {
unordered_set mb; //设置一个set集合用于存放B,消除B中的重复元素
vector ans;
int SumA=0,SumB=0;
for(int i=0;i0){ //在B中检测大小为y的糖果是否存在
//若存在则将相应大小x,y放入数组(x,y是满足上述公式的)。
ans.push_back(A[i]);
ans.push_back(del);
break;
}
}
return ans;
}
};
⑤. 905. 按奇偶排序数组(双向双指针)----------------------------------------------------------------------------------------------------------------------------------
给定一个非负整数数组 A,返回一个数组,在该数组中, A 的所有偶数元素之后跟着所有奇数元素。你可以返回满足此条件的任何数组作为答案。
| 输入 | 输出 | 解释 |
|---|---|---|
| [3,1,2,4] | [2,4,3,1] |
思路:设置两个同向指针left和right 使得 left 永远指向从数组头部往后的第一个奇数。
而 right 永远指向从数组尾部往前的第一个偶数。
class Solution {
public:
vector sortArrayByParity(vector& A) {
int left=0;
int right=A.size()-1;
while(left0 && A[right]%2!=0) // right永远指向从数组 尾部往前 的第一个偶数。
right--;
if(left>=right)
break;
swap(A[left],A[right]); //交换奇数和偶数
}
return A;
}
};
⑥. 202. 快乐数
编写一个算法来判断一个数是不是“快乐数”。
一个“快乐数”定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是无限循环但始终变不到 1。如果可以变为 1,那么这个数就是快乐数。
| 输入 | 输出 | 解释 |
|---|---|---|
| 19 | true |
思路:若一个数是快乐数,则这个数最终会变为1,且开始无限循环。因此,可以通过判断是否有循环来判断是否是快乐数。要判断是否存在循环,可以通过双指针算法。当进入循环后,两个指针总会相遇。
class Solution {
public:
bool isHappy(int n) {
int slow=n;
int fast=n;
do{
slow=bitsum(slow); //慢(指针)每次计算一次
fast=bitsum(fast); //快指针每次计算两次
fast=bitsum(fast);
}while(slow!=fast); //当快指针与慢指针相遇时,判断慢指针此时是否为1,若是,则说明次数为快乐数
return slow==1;
}
int bitsum(int n){
int sum=0;
while(n>0){
int bit= n % 10;
sum += bit * bit;
n=n / 10;
}
return sum;
}
};
4. Majority Element问题(数组中出现次数最多的元素)
Majority Element问题主要描述的是计算数组中出现次数最多的元素,如计算一个数组中的众数(元素出现次数>[n/2]),计算一个数组中元素出现次数>[n/3]的元素。
Majority Element问题
①. 169. 求众数-------------------------------------------------------------------------------------------------------------------------------------------------------------
给定一个大小为 n 的数组,找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。你可以假设数组是非空的,并且给定的数组总是存在众数。
| 输入 | 输出 | 解释 |
|---|---|---|
| [2,2,1,1,1,2,2] | 2 |
思路:这一类问题采用摩尔投票法进行求解,摩尔投票法的核心就是对拼消耗,因为是寻找数组中超过一半的数字,这意味着数组中其他数字出现次数的总和都是比不上这个数字出现的次数 。如果把该众数记为 +1 ,把其他数记为 −1 ,相当于抵消了一个,将它们全部加起来,和是大于 0 的。
class Solution {
public:
int majorityElement(vector& nums) {
int target=nums[0]; //默认第一个元素为target
int count=1;
for(int i=1;i 5. 抽屉(鸽巢)/一个萝卜一个坑问题
所谓抽屉问题,就是一个萝卜一个坑。运用抽屉原理的核心是分析清楚问题中,哪个是物件,哪个是抽屉。
抽屉问题性质:
(1).把多于n+1个的物体放到n个抽屉里,则至少有一个抽屉里的东西不少于2件。
(2).把多于m*n+1个物体放到n个抽屉,则至少有一个抽屉里有不少于(m+1)的物体。
(3).把(m*n)-1个物体放到n个抽屉中,其中必有一个抽屉中至多m-1个物体
一个萝卜一个坑问题
①. 448. 找到所有数组中消失的数字------------------------------------------------------------------------------------------------------------------------------------
给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组,数组中的元素一些出现了两次,另一些只出现一次。找到所有在 [1, n] 范围之间没有出现在数组中的数字。
在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务。 你可以假定返回的数组不算在额外空间内。
| 输入 | 输出 | 解释 |
|---|---|---|
| [4,3,2,7,8,2,3,1] | [5,6] |
思路:
Method1:
由于数组范围为 1 ≤ a[i] ≤ n ,即一个萝卜一个坑,a[0]=1,a[1]=2...a[n]=n+1,且a[n]=a[a[n]-1]要找到数组中消失的数字,只需要将每个数字放到对应的位置,然后遍历数组,若位置上不是对应的数时,即为缺失的数字。
step1:遍历数组,若nums[i]!=nums[nums[i]],则交换两个数,直到遍历结束。这时,每个数字就放到其对应的位置上了。
step2:再次遍历数组,如果nums[i]!=i-1,则其下标就为空缺的数。
class Solution {
public:
vector findDisappearedNumbers(vector& nums) {
vectorans;
if(nums.empty())
return nums;
for(int i=0;i Method2:
step1:将数组元素对应为索引的位置加nums.size(),对于排序后完整数组,所有的数都应该大于nums.size()。
step2:遍历加nums.size()后的数组,若数组元素值小于等于nums.size(),则说明数组下标值不存在,即消失的数字。
class Solution {
public:
vector findDisappearedNumbers(vector& nums) {
vectorans;
if(nums.empty())
return nums;
for(int i=0;i 6. 动态规划问题
动态规划遵循一套固定的流程:递归的暴力解法 -> 带备忘录的递归解法 -> 非递归的动态规划解法。动态规划算法就是根据这一个流程层层深入而得到的。下面以“斐波那契数”问题来介绍动态规划算法是如何得到的。
6.1 斐波那契数列
斐波那契数,通常用 F(n) 表示,形成的序列称为斐波那契数列。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1.斐波那契数的状态转移方程:
f ( n ) = { 0 n=0 || n=1 f ( n − 1 ) + f ( n − 2 ) n>0 f(n)= \begin{cases} 0& \text{n=0 || n=1}\\ f(n-1)+f(n-2)& \text{n>0} \end{cases} f(n)={0f(n−1)+f(n−2)n=0 || n=1n>0
动态规划算法是如何得到:
思路:
step1: 递归暴力解法:
递归暴力解法就是根据状态转移方程直接进行计算。
class Solution {
public:
int fib(int N) {
if(N==0)
return 0;
if(N==1||N==2)
return 1;
return fib(N-1)+fib(N-2); //进行递归求解
};
step2: 带备忘录的递归解法:
在递归算法中,斐波那契数问题存在大量的重复计算,为了消除冗余计算,增加一个“备忘录”来记录运算的结果,每次运算之前先读取备忘录,如不存在在进行计算。时间复杂度为(O(n))。带备忘录的递归解法是一种<自顶向下>的算法。
class Solution {
public:
int fib(int N) {
if(N==0)
return 0;
vector temp(N+1,0); //设置一个数组(备忘录)用于存放已经计算过的数
return helper(temp,N);
}
int helper(vector &temp,int N){
if(N==1||N==2)
return 1;
if(temp[N]!=0) //如果备忘录中不为0,则说明该数计算过,直接读取计算结果就行
return temp[N];
temp[N]=helper(temp,N-1)+helper(temp,N-2); //备忘录不存在,进行计算
return temp[N];
}
};
step3: 非递归的动态规划解法:
动态规划(dp)算法是一种<自顶向上>的算法。动态规划的另一个重要特性是最优子结构,所谓最优子结构就是原问题的解由子问题的最优解构成且子问题间必须互相独立。
class Solution {
public:
int fib(int N) {
if(N<2)
return N;
int pre=0;int cur=1;
for(int i=2;i<=N;i++){
int sum=pre+cur;
pre=cur;
cur=sum;
}
return cur;
};
6.2 背包问题
6.3 其他动态规划问题
① 746. 使用最小花费爬楼梯---------------------------------------------------------------------------------------------------------------------------------------------
数组的每个索引做为一个阶梯,第 i个阶梯对应着一个非负数的体力花费值 cost[i](索引从0开始)。每当你爬上一个阶梯你都要花费对应的体力花费值,然后你可以选择继续爬一个阶梯或者爬两个阶梯。您需要找到达到楼层顶部的最低花费。在开始时,你可以选择从索引为 0 或 1 的元素作为初始阶梯。
| 输入 | 输出 | 解释 |
|---|---|---|
| cost = [10, 15, 20] | 15 | 最低花费是从cost[1]开始,然后走两步即可到阶梯顶,一共花费15。 |
| cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] | 6 | 最低花费方式是从cost[0]开始,逐个经过那些1,跳过cost[3],一共花费6。 |
思路:这道题可能在题目的理解上有些绕,题中cost使每个台阶需要消耗的体力值,每次上台阶可以上一个台阶,也可以上两个台阶,计算到达顶部时最低消耗的体力值。
初次面对问题,不可能一眼就看出是动态规划问题,需要一步步对问题进行分析:设第n阶梯的总体力值为dp[n]则:
① dp[0]=cost[0] ②dp[1]=cost[1] //一次上两个台阶
③ dp[2]=min(dp[0],dp[1])+cost[2] //可以在0台阶一次上两个台阶得到,也可以在1台阶上一个台阶得到
④ dp[3]=min(dp[2],dp[1])+cost[3] …
最终得到状态方程为:dp[n]=min(dp[n-1],dp[n-2])+cost[n], 由方程可以发现,当前状态只和前两个状态有关,所以用动态规划求解
class Solution {
public:
int minCostClimbingStairs(vector& cost) {
if(cost.size()==0)
return 0;
int pre=cost[0]; //存放前一次结果
```powershell
int current=cost[1]; //存放当前结果
for(int i=2;i 7. 滑动窗口方法
滑动窗口算法是通过使用特定大小的子列表(固定大小的窗口),在遍历完整列表的同时进行特定的操作,以达到降低了循环的嵌套深度。
滑动窗口问题
① 643. 子数组最大平均数 I(这个问题设置了子序列的长度)--------------------------------------------------------------------------------------------------
给定 n 个整数,找出平均数最大且长度为 k 的连续子数组,并输出该最大平均数。
| 输入 | 输出 | 解释 |
|---|---|---|
| [1,12,-5,-6,50,3], k = 4 | 12.75 | 最大平均数 (12-5-6+50)/4 = 51/4 = 12.75 |
思路:这道题看似和“最大子序列和”问题类似,但是该问题在其基础上设置了子序列的长度k,因此,原有的贪心算法就不适合了,但是由于设置了子序列长度,可以通过滑动窗口算法来求解此题。
class Solution {
public:
double findMaxAverage(vector& nums, int k) {
int sum=0;
int ans=-INT_MAX;
for(int i=0;i 8. 散列集合问题
STL中的散列集合
在C++ STL中包含多种类型的散列集合(关联容器),如map,undered_map,set,undered_set等等。
(1). set
set在底层使用平衡的搜索树—红黑树实现,只保存关键字key,set主要有以下几个特点:
① set在插入删除操作时不需要内存移动和拷贝。
② set中的元素是唯一的(不能有重复元素),默认对元素自动进行升序排列。
③ 不能直接修改set容器中元素的值。要修改某元素的值,需要先删除该元素,再插入新元素。
④ set的常用操作:
使用时注意包含头文件 #include <set>
s.begin() 返回set容器的第一个元素的迭代器
s.end() 返回set容器的最后一个元素迭代器
s.clear() 删除set容器中的所有的元素
s.empty() 判断set容器是否为空
s.insert() 插入一个元素
s.erase() 删除一个元素
s.size() 返回当前set容器中的元素个数
(2). unordered_set
unordered_set基于哈希表实现,数据插入和查找时间复杂度低,但空间复杂度较高。unordered_set的特点如下:
① unordered_set无自动排序功能
② unordered_set无法插入相同的元素
③ unorder_set的常用操作:
使用时注意包含头文件 #include <unordered_set>
us.begin() 返回unordered_set容器的第一个元素的迭代器
us.end() 返回unordered_set容器的最后一个元素迭代器
us.clear() 删除unordered_set容器中的所有的元素
us.empty() 判断unordered_set容器是否为空
us.insert() 插入一个元素
us.erase() 删除一个元素
us.size() 返回当前set容器中的元素个数
us.count() 返回unordered_set中元素的个数,只能是0或1
(3). map
map提供一对一的hash,能够建立key-value一一对应的关系,map内部基于红黑树建立。在map中的元素是基于pair的,map内部的所有数据都是有序的。
map常用操作:
使用时注意包含头文件 #include <map>
m.begin() 返回map容器的第一个元素的迭代器
m.end() 返回map容器的最后一个元素迭代器
m.clear() 删除map容器中的所有的元素
m.empty() 判断map容器是否为空
m.insert(pair<>) 插入一个pair元素
m.find() 查找一个元素
m.erase() 删除一个元素
m.rbegin() 返回一个指向map尾部的逆向迭代器
m.rend() 返回一个指向map头部的逆向迭代器
m.size() 返回当前map容器中的元素个数
m[] / m.at() 访问元素
(4). unordered_map
unordered_map内部元素是无序的。
unordered_map常用操作:
使用时注意包含头文件 #include <unordered_map>
um.begin() 返回unordered_map容器的第一个元素的迭代器
um.end() 返回unordered_map容器的最后一个元素迭代器
um.clear() 删除unordered_map容器中的所有的元素
um.empty() 判断unordered_map容器是否为空
um.insert(pair<>) 插入一个pair元素
um.find() 查找一个元素
um.erase() 删除一个元素
um.rbegin() 返回一个指向unordered_map尾部的逆向迭代器
um.rend() 返回一个指向unordered_map头部的逆向迭代器
um.size() 返回当前unordered_map容器中的元素个数
um[] / m.at() 访问元素
散列集合方法
在应用HashTable方法进行问题求解时,注重的是对HashTable方法的理解。具体的要学习HashTable数据结构。
① 697. 数组的度------------------------------------------------------------------------------------------------------------------------------------------------------------
给定一个非空且只包含非负数的整数数组 nums, 数组的度的定义是指数组里任一元素出现频数的最大值。你的任务是找到与 nums 拥有相同大小的度的最短连续子数组,返回其长度。
| 输入 | 输出 | 解释 |
|---|---|---|
| [1, 2, 2, 3, 1] | 2 | 最大平均数 (12-5-6+50)/4 = 51/4 = 12.75输入数组的度是2, 因为元素1和2的出现频数最大,均为2. 连续子数组里面拥有相同度的有如下所示:[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]最短连续子数组[2, 2]的长度为2,所以返回2. |
思路:
class Solution {
public:
int findShortestSubArray(vector& nums) {
unordered_map index; // index计算每个元素出现的个数,以元素为key,元素个数为value
unordered_map> pos; //pos存储第一个元素和最后一个元素的位置,
//元素为key, pair中第一个int为第一次出现位置,第二个int为第二次出现位置
int degree=0;
int ans=INT_MAX;
for(int i=0;i ② 1. 两数之和----------------------------------------------------------------------------------------------------------------------------------------------------------------
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
| 输入 | 输出 | 解释 |
|---|---|---|
| 给定 nums = [2, 7, 11, 15], target = 9 | [0, 1] | 最大平均数 (12-5-6+50)/4 = 51/4 = 12.75输入数组的度是2, 因为元素1和2的出现频数最大,均为2. 连续子数组里面拥有相同度的有如下所示:[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]最短连续子数组[2, 2]的长度为2,所以返回2. |
思路:利用unordered_map来存储每个索引计算的差值,再次计算差值后在unordered_map中进行查找,如果查找到则输出当前索引和对应差值的索引值。
class Solution {
public:
vector twoSum(vector& nums, int target) {
unordered_map record;
vectorans;
for(int i=0;i(res,res+2);
}
record[nums[i]] = i;
}
return ans;
}
};
③ 349. 两个数组的交集
给定两个数组,编写一个函数来计算它们的交集。
| 输入 | 输出 | 解释 |
|---|---|---|
| nums1 = [1,2,2,1], nums2 = [2,2] nums1 = [4,9,5], nums2 = [9,4,9,8,4] |
[2] [9,4] |
思路:从例子中可以发现,nums1和nums2两个数组中有重复的数据,因此在计算两个数组的相同元素的同时,还要将重复的数据进行删除。查找元素的交集可以利用双指针法,将查找后元素放入到set集合中,可以去除重复的元素。
class Solution {
public:
vector intersection(vector& nums1, vector& nums2) {
int n1=0;
int n2=0;
set s;
vector ans;
sort(nums1.begin(),nums1.end());
sort(nums2.begin(),nums2.end());
while(n1nums2[n2])
n2++;
else{
s.insert(nums1[n1]); //将查找后元素放入到set集合中,可以去除重复的元素
n1++;
n2++;
}
}
set::iterator iter=s.begin();
for(int i=0;i 9. 排序问题
排序问题是一个"古老而经典"的问题。
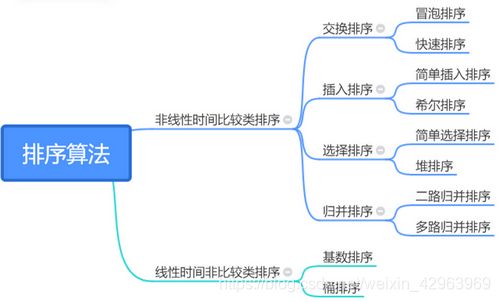
排序问题的分类:
| 算法 | 平均时间复杂度 | 最好 | 最差 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序(交换两个相邻数的大小顺序) | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 选择排序(在数组中找到最小的一个数,与已经排序后的第一个数交换) | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 插入排序(通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入) | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 希尔排序 | O(nlogn) | O(n(logn^2)) | O(n(logn^2)) | O(1) | 不稳定 |