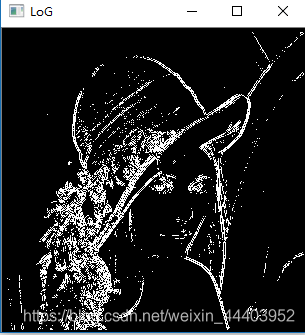
边缘检测之LoG算子(高斯-拉普拉斯算子)
-
原理
LoG算子是由拉普拉斯算子改进而来。拉普拉斯算子是一个单纯的二阶导数算子,是一个标量,具有线性、位移不变性,其传函在频域空间的原点为0。所有经过拉普拉斯算子滤波的图像具有零平均灰度。但是该算子的缺点是 对噪声具有无法接受的敏感性,因此在实际应用中,一般先要对图像进行平滑滤波,再用拉氏算子进行图像的边缘检测。这就是LoG算子的产生的背景(最后的梯度表达式为 高斯函数和原图像卷积,再去二阶微分算子)。
其滤波函数模型为:

因此,在设计卷积模板时,应该按照该函数的对称性设计,便可以来近似获得该函数的卷积效果。
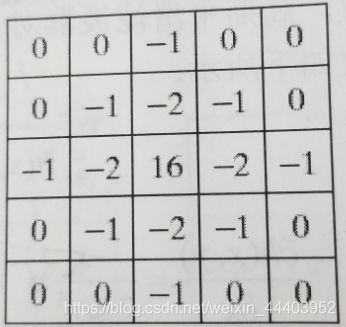
这里卷积模板取的5阶,如下模型。
-
实现算法
import numpy as np
import cv2
from matplotlib import pyplot as plt
#定义掩膜
m1 = np.array([[0,0,-1,0,0],[0,-1,-2,-1,0],[-1,-2,16,-2,-1],[0,-1,-2,-1,0],[0,0,-1,0,0]]) #LoG算子模板
img = cv2.imread("lena_1.tiff",0)
#边缘扩充
image = cv2.copyMakeBorder(img, 2, 2, 2, 2, borderType=cv2.BORDER_REPLICATE)
# image = cv2.GaussianBlur(img,(3,3),4)
rows = image.shape[0]
cols = image.shape[1]
temp = 0
image1 = np.zeros(image.shape)
for i in range(2,rows-2):
for j in range(2,cols-2):
temp = np.abs(
(np.dot(np.array([1, 1, 1, 1, 1]), (m1 * image[i - 2:i + 3, j - 2:j + 3])))
.dot(np.array([[1], [1], [1], [1], [1]])))
image1[i,j] = int(temp)
if image1[i, j] > 255:
image1[i, j] = 255
else:
image1[i, j] = 0
cv2.imshow("LoG",image1)
cv2.waitKey(0)
- lena效果图