数据结构（三） 栈和队列

刚才发现一个网站上，讲栈讲的特别好，给大家推荐下

http://www.nowamagic.net/librarys/veda/detail/2270

一、 填空

1、循环队列队满的条件是（　front ==（rear+1）mod n　 ），队空的条件是（ rear == front　）。

解释：

请参考这篇博文http://blog.csdn.net/huangkq1989/article/details/5719529

2、设有一个空栈，栈顶指针为1000H，现有输入序列为1、2、3、4、5， 经过push，push，pop，push，pop，push，push后，输出序列是（ 23 　），栈顶指针是（ 1003H　 ）。

解释：

切记push操作是往栈顶插入元素，而pop操作是删除栈顶元素，即把栈顶元素输出。

push	push /pop	push/pop	push	push
1	2	3	4	5
1000H	1001H	1001H	1001H	1002H

栈顶指针在栈顶元素的下一个位置上

3、设一个链栈的栈顶指针为ls，栈中结点两个字段分别为data和next，其中next是指示后继结点的指针，栈空的条件是（ ls=Null ），如果栈不空，则退栈操作为p=ls；（ ls=ls->next ）；free（p）。

解释：

栈顶指针Is为Null，即栈为空栈，这个需要记住

退栈的话，形象点说，就是把栈里面的往外推，后进先出的原则

p=ls;//把栈顶指针ls赋值给p
ls=ls->next;//改变栈顶指针的值为它的后继指针
free（p）;//释放p

4、栈和队列是两种特殊的线性表，栈的特点是（ 后进先出 ），队列的特点是（ 先进先出 ），二者的共同点是只允许在它们的（ 端点 ）处插入和删除数据元素。

解释：

这个就是它们的特点，记住就好！

5、栈结构通常采用的两种存储结构是（ 顺序存储和链式存储 ）；其判定栈空的条件分别是（ top == 0和top == null ），判定栈满的条件分别是（top == maxsize 和 内存无可用空间 ）。

解释：
记住顺序存储的原理是数组，链式存储的原理是指针。

6、（ 栈 ）可作为实现递归函数调用的一种数据结构。

解释：

自己看书，没啥好解释的。

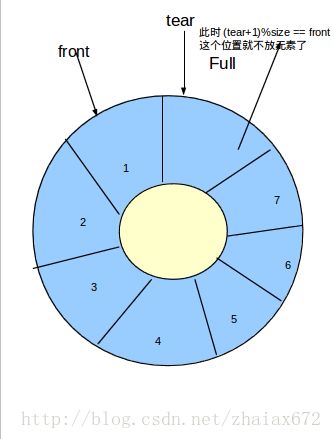
7、数组Q[n]用来表示一个循环队列，f为当前队头的前一个位置，r为队尾元素的位置，计算队列中元素个数的公式为（ （r-f+n）mod n ）。

解释：

如图，f=0，r=7,n=8。（r-f+n） mod n =(7-0+8) mod 8 =7。公式得证！

8、循环队列的引入是为了克服（ 假溢出 ）。

解释：

这个很简单，自己想。

9、表达式a*(b+c)-d的后缀表达式是（ abc+*d- ）。

解释：

http://www.nowamagic.net/librarys/veda/detail/2306，这个是个很不错的网站！！

二、 选择题

1、若一个栈的输入序列是1，2，3……n，输出序列的第一个元素是ｎ，则第ｉ个输出元素是（　D　）。

Ａ、不确定 B、n-i C、n-i-1 D、n-i+1

不解释，自己去试！

2、设数组SQ[m]作为循环队列SQ的存储空间，front为队头指针，rear为队尾指针，则执行出队操作的语句为（ B ）

A：front++ B：front=（front+1） mod 　m
C：rear=（rear+1）mod m D：front=（front+1）mod （m+1）

解释：按照先进先出的原则，就是不停地把队头指针的下一个指针赋值给它

３、链栈与顺序栈相比有一个明显的优点是（　B　　）。

Ａ：插入操作更加方便　　　Ｂ：通常不会出现栈满的情况
Ｃ：不会出现栈空的情况　　Ｄ：删除操作更加方便

解释：
顺序存储 栈空的条件 top == 0；栈满的条件 top == maxsize【数组，懂吧】
链式存储 栈栈空的条件 top == null ；栈满的条件 内存无可用空间 【指针，懂吧】

4、判定一个顺序栈ST（最多元素为m）为空的条件是（ B ），栈满的条件是（ D ）。
A：STtop!=0 B：STtop= =0 C：STtop!=m D：STtop= =m

参照上一题。。。

5、判定一个顺序队列QU（最多元素为m）为空的条件是（ C ），队满的条件是（ A ）。

A：QU->rear-QU->front= =m B：QU->rear-QU->front-1= =m
C：QU->front= =QU->rear D：QU->front= =QU->rear+1

这个应该很好想吧

6、判定一个循环队列QU（最多元素为m）为空的条件是（ A ），队满的条件是（ C ）。

A：QUrear= =QUfront B：QUrear！=QUfront
C：QUfront= =（QUrear+1）%m D：QUfront! =(QUrear+1)%m

参照填空第一题

7、设栈Ｓ和队列Ｑ的初始状态为空，元素e1、e2、e3、e4、e5、e6依次通过栈Ｓ，一个元素出栈后即进入队列Ｑ，若６个元素出列的顺序是e2、e4、e3、e6、e5、e1，则栈Ｓ的容量至少应该是（　C　 ）。

Ａ：６　　　　Ｂ：４　　　　Ｃ：３　　　　Ｄ：２

参照填空题第二道

8、一个栈的入栈序列是1，2，3，4，5，则栈的不可能的输出序列是（ C ）。

A：54321 B：45321 C：43512 D：12345

解释：先进后出，一个个试一下

9、设计一个判别表达式中左右括号是否配对的算法，采用（ B ）数据结构最佳。

A：顺序表 B：栈 C：队列 D：链表

解释：没错，这个又是书上的栈的一个应用

10、一个队列的入队顺序是1，2，3，4，则队列的输出顺序是（ B ）。

A：4321 B：1234 C：1432 D：3241

解释：先进先出

11、栈和队的主要区别在于（ D ）。

A：它们的逻辑结构不一样 B：它们的存储结构不一样
C：所包含的运算不一样 D：插入、删除运算的限定不一样

解释：
栈（Stack）是限定只能在表的一端进行插入和删除操作的线性表。
队列（Queue）是限定只能在表的一端进行插入和在另一端进行删除操作的线性表。

12、设数组S[n]作为两个栈S1和S2的存储空间，对任何一个栈只有当S[n]全满时才不能进行进栈操作。为这两个栈分配空间的最佳方案是（ A ）。

A：S1的栈底位置为0，S2的栈底位置为n-1
B：S1的栈底位置为0，S2的栈底位置为n/2
C：S1的栈底位置为0，S2的栈底位置为n
D：S1的栈底位置为0，S2的栈底位置为1

解释：
利用栈底位置不变的特性，可让两个顺序栈共享一个一维数据空间，以互补余缺，实现方法是：将两个栈的栈底位置分别设在存储空间的两端，让它们的栈顶各自向中间延伸。这样，两个栈的空间就可以相互调节，只有在整个存储空间被占满时才发生上溢，这样一来产生上溢的概率要小得多。

三、 算法设计

1、 以标志变量flag作为判断循环队列空或满的依据，写出循环队列中插入和删除的算法。

分析：设标志flag=0表示队空，flag=1表示队不空。则队空条件为(rear=front)&&(flag=0)，队满条件为(rear=front)&&(flag=1)。

（1）插入算法：
void  insert (sqQueue  sq ,  QElemType  x) {

   if  ((sq.rear= =sq.front)&&(flag= =1))

        error(‘overflow’);

   else  {
            flag=1;
            sq.rear=(sq.rear+1)%maxqsize;
            sq.data[sq.rear]=x ;

              }

}//insert

(2)删除算法：

void  delete (sqQueue  sq ) {

  if ((sq.rear= =sq.front)&&(flag= =0)

      error(“underflow’);

       else  {

                flag=0;
                sq.front=(sq.front+1)%maxqsize;
                x=sq.data[sq.front];

         }

}//delete

2、 假设以不带头结点的循环链表表示队列，并且只设一个指针指向队尾结点，但不设头指针。试设计相应的入队和出队的算法。

分析：出队操作是在循环单链表的头部进行，相当于删除首结点，而入队操作是在循环单链表的尾部进行，相当于在终端结点后插入一个结点。算法如下：

（1）入队算法：
        void  enqueue( QueuePtr  rear,  Qelemtype  x ) {
          s=( QueuePtr)malloc(sizeof (Qnode));
          sdata=x;
          if (rear= =Null) { rear=s;
                         rearnext=s;}
else  {snext=rearnext;
                rearnext=s;
                rear=s;
                }
        }//enqueue

(2) 出队算法：
void  delqueue (QueuePtr  rear, Qelemtype  x) {
  if (rear= =Null) return ERROR;
  else  { s=rearnext;
        if (s= =rear)  rear=Null;
        else  rearnext=snext;
        x=s->data;
        free(s);
             }
}//delqueue

加油！！