spss实现中心化处理、标准化处理和归一化处理

一、中心化、标准化、归一化简单描述

1. 意义：数据中心化和标准化在回归分析中是取消由于量纲不同、自身变异或者数值相差较大所引起的误差。
2. 原理：
   数据标准化：是指数值减去均值，再除以标准差；
   数据中心化：是指变量减去它的均值。
   归一化：把数变为（0，1）之间的小数

二、中心化处理

        数据的中心化是指原数据减去该组数据的平均值，经过中心化处理后，原数据的坐标平移至中心点（0,0），该组数据的均值变为0，以此也被称为零均值化。

        简单举例：譬如某小公司老板员工共5人，5人的工资,分别为12000、5000、8000、3000、4000元，这5个数据作为一个独立的数据集，平均值为6400元，每个人的工资依次减去平均水平6400，得到5600、-1400、1600、-3400、-2400，新的5个数据其平均值等于0，这个过程就是数据的中心化。

        下面详细讲解在SPSS中的操作步骤。

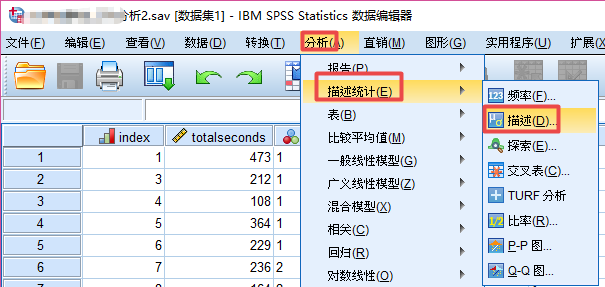
        第一步：在分析选择描述统计，接着选择描述。

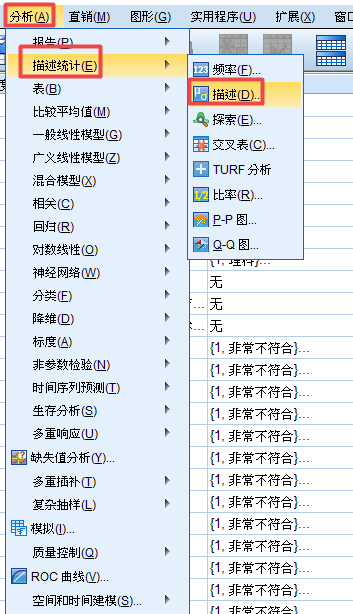
        第二步：选择所要分析的变量，在选项中勾选平均值即可。

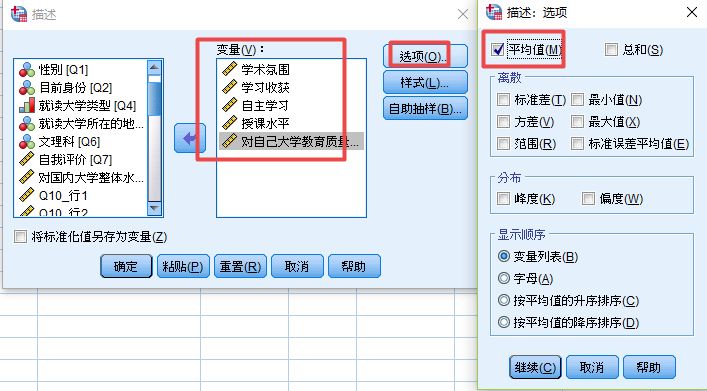
        输出得到每个变量的平均值如下

描述统计
	个案数	平均值
学术氛围	191	15.9843
学习收获	191	16.3351
自主学习	191	13.4241
授课水平	191	23.5864
对自己大学教育质量评价	191	66.69
有效个案数	191

        第三步：在工具栏区，在转换中选择计算变量

        这里，我们第一个计算的是 授课水平这个变量，一开始先给中心化后的变量命名，接着选择变量，然后在输出的结果复制这个变量的平均值（建议直接复制过去），粘贴到数学表达式里面

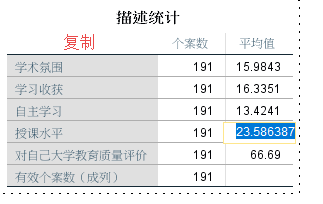
        我们第二个计算的是对自己大学教育质量评价这个变量，步骤同第一个变量。

        最后，我们得到得到两个新的中心化处理的变量。

        我们把这两个变量和新变量的描述性统计数据输出，查看它们的变化结果。

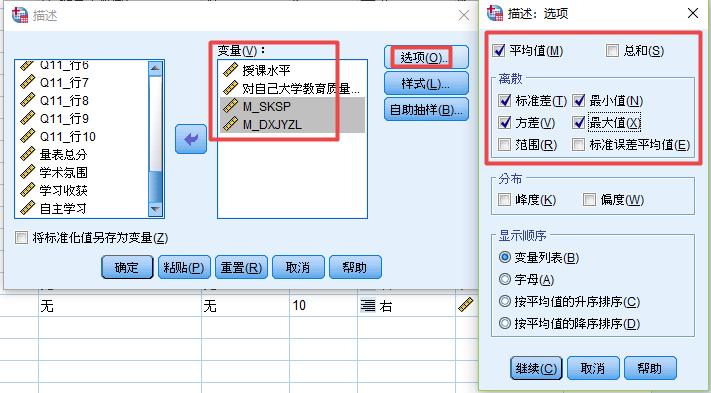
        我们可以发现，它们的最大值和最小值都发生了改变，并且新变量的均值均为0，这是因为新的两个变量都用变量中的每个值减去均值，所以均值为0，而且我们可以发现它们的标准差和方差都没有发生变化，说明这个数据的形态和分布情况是没有发生改变的，只是平均值进行了移动。

三、标准化处理

        大型数据分析项目中，数据来源不同，量纲及量纲单位不同，为了让它们具备可比性，需要采用标准化方法消除由此带来的偏差。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。这就是数据标准化。

        基本原理：数值减去平均值，再除以其标准差，得到均值为0，标准差为1的服从标准正态分布的数据。

        在SPSS中，使用最多的就是Z-score标准化（0-1标准化）方法，这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1。

        在SPSS的处理步骤如下：

        第一步：在分析中选择描述统计，接着选择描述。

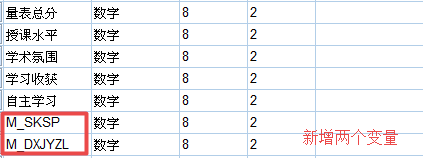
        第二步：选择所要标准化的变量。在下面勾选将标准化值另存为变量（Z），点击确定。

        我们可以在变量视图发现这个时候新增加了标准化后的三个变量。

四、归一化处理

归一化方法：

1. 把数变为（0，1）之间的小数
   主要是为了数据处理方便提出来的，把数据映射到0～1范围之内处理，更加便捷快速
2. 把有量纲表达式变为无量纲表达式
   归一化是一种简化计算的方式，即将有量纲的表达式，经过变换，化为无量纲的表达式，成为纯量。

        归一化，也算是数据标准化方法之一。常见的计算公式如下，得到新数据范围在[0,1]之间，归一化由此得名。
$$x^{\ast }=\frac{x-min}{max-min}$$

        在SPSS的操作步骤如下：

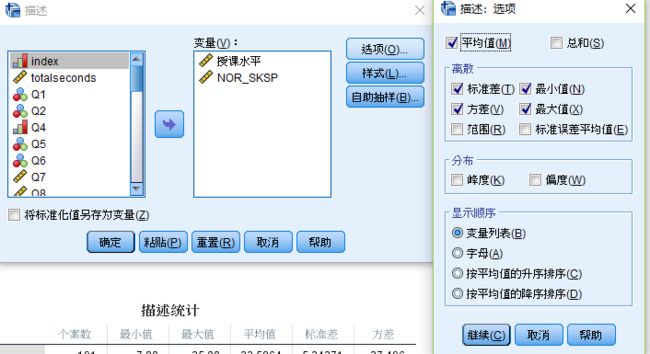
        第一步：在分析选择描述统计，接着选择描述。

第二步：选择变量和指定输出最大值和最小值。         第三步：在**转换**中选择**计算变量**。

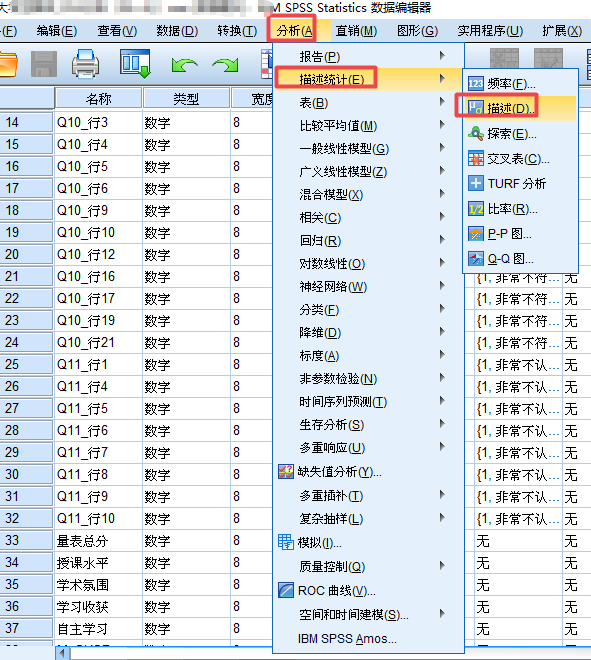
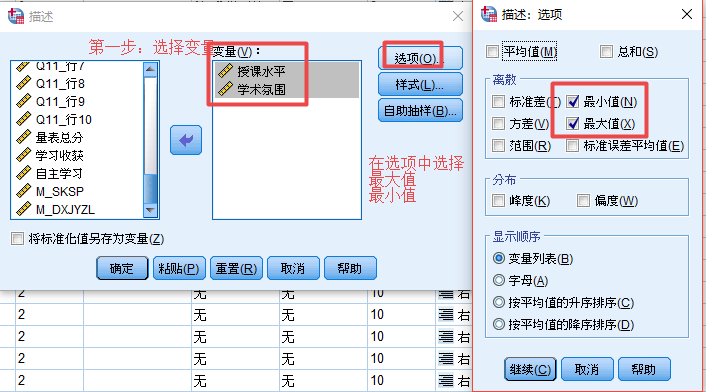
        接着在表达式中输入相应的计算公式

        可直接在输出窗口复制最大值和最小值。

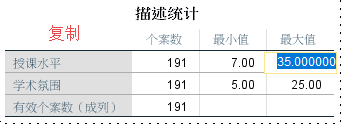
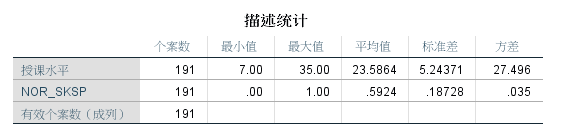
        我们可以在描述统计里面查看授课水平和归一化处理后变量的统计结果的区别。

        我们可以看到，归一化后，新数据范围在[0,1]之间。

五、参考资料

• 什么是数据标准化、中心化、归一化？SPSS又如何实现？
• 数据的中心化、标准化和归一化