浅谈内插波束形成
引言
对于一个模拟信号进行采样,其采样间隔通常大于Nyquist频率。亦即对于一个最高频率为f的信号,从恢复信号波形的角度出发,采样频率必须大于最高频率的两倍。然而,在数字波束形成器中,采用数字延迟线,其延迟量化单元即为采样周期。这个量化的采样周期,如果正好使其方位波束要求的各延迟补偿值得到的波束相同。否则,波束指向不准,同时波束图会发生畸变。由此可知,按同步波束要求,输入信号的最大采样周期应由最小波束控制角决定。这一采样周期为T_s=T_min=(d/c)sinθ_min,此值决定的输入信号采样频率远远大于恢复波形所需的Nyquist频率。而从恢复波形的角度出发,波束形成器输出采样频率只要满足Nyquist频率的要求即可,无需更高的采样率。因此能否既不提高输入信号采样频率,又能保证波束形成足够精确。R.G.Pridham建议的数字内插波束形成技术就是解决这一问的方法之一。
数字内插滤波原理
若信号波形按采样定理以f_N=1/Δ的频率进行采样,则可用内插滤波器实现再采样,得到采样频率升高为f_B=1/δ=Lf_N的序列,具体过程如下。
设输入信号为x(t),按f_N采样后,得到序列x(n)=x(nΔ)。在两个采样点间补L-1个零点,L称为内插比。经补零后的序列为V(m)=v(mδ),其中δ=Δ/L,即 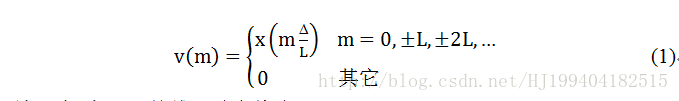
记输入序列x(nΔ)的傅里叶变换为 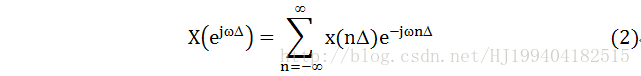
则v(mδ)的傅里叶变换为 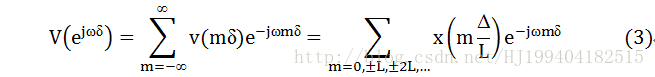
(3)式说明以Δ间隔采样的序列x(nΔ)与补零后的序列v(mδ)的谱形状是相同的。
另一方面,若以采样率1/δ对x(t)进行采样,得到序列x(nδ),其傅里叶变换为 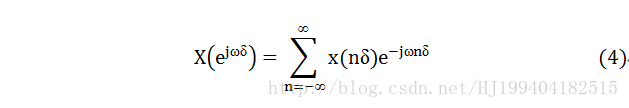
可见,X(e^jωδ )与V(e^jωδ )在ω=±k(2π/δ)处(k=1,2,…)是相同的,所以,若将V(e^jωδ )通过一理想低通滤波器,即可由v(nδ)转换为x(nδ)。
数字内插波束形成器的结构
有两种形式第一种是先内插滤波,后波束形成;第二种是先波束形成,后内插滤波。由于整个过程是线性过程,所以这两种形式是等效的。 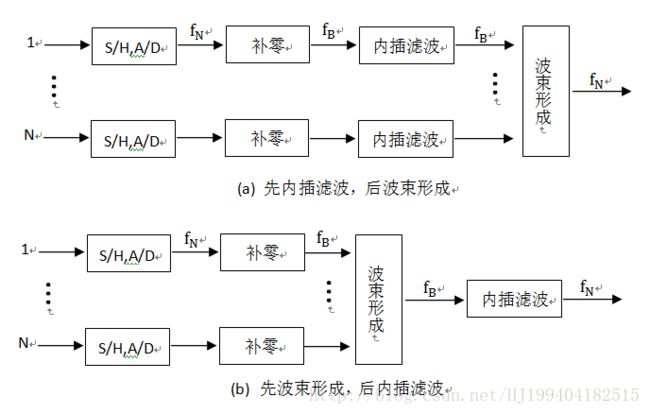
CW脉冲信号内插Matlab仿真分析
以下是仿真的程序
clear all;
close all;
clc;
f0 = 150e3; %信号频率
fs = 5*f0; %采样率
tao = 1e-4; %信号持续的时间
D = 20; %定义上采样倍数
ts = 0:1/fs:tao; %信号持续时间点
sin_signal = sin(2*pi*f0*ts);
num_ts = length(ts);
t = (0:num_ts*10-1)/fs; %时间点
cw_signal = zeros(1,num_ts*10);
cw_signal(num_ts*5:num_ts*6-1)=sin_signal;
F = (0:num_ts*10-1)*fs/(num_ts*10); %频率点
figure;
plot(t,cw_signal);
title('原始CW信号');
xlabel('时间t/s');
figure;
plot(F,abs(fft(cw_signal)));
title('原始CW信号频谱');
xlabel('频率Hz');
t_D = (0:num_ts*10*D-1)/(fs*D);
cw_signal_D = zeros(1,num_ts*10*D);
cw_signal_D(1:D:num_ts*10*D) = cw_signal;
F_D = (0:num_ts*10*D-1)*fs*D/(num_ts*10*D);
figure;
plot(t_D,cw_signal_D);
title('被插D-1个0后的CW信号');
xlabel('时间t/s');
figure;
plot(F_D,abs(fft(cw_signal_D)));
title('被插D-1个0后的CW信号频谱');
xlabel('频率Hz');
%********************************************************************************
%低通滤波
N=64; %滤波器的阶数
wc=pi*200e3/(fs*D/2); %截止频率 200KHz
n=0:N-1;
r=(N-1)/2;
hdn = sin(wc*(n-r))/pi./(n-r);
if rem(N,2)~=0
hdn(r+1)=wc/pi;
end
wn = hamming(N); %hamming窗
hn = hdn.*wn';
LPF_cw_signal_D = filter(hn,1,cw_signal_D);
figure;
plot(t_D,LPF_cw_signal_D);
title('被插D-1个0后再经过低通滤波器的CW信号');
xlabel('时间t/s');
figure;
plot(F_D,abs(fft(LPF_cw_signal_D)));
title('被插D-1个0后再经过低通滤波器的CW信号频谱');
xlabel('频率Hz');运行一下程序得到如下的图片
信号的中心频率为150KHz,以五倍于它的频率对他进行采样。得到如下图所示的原始CW脉冲信号,右边的图片展示的为信号的细节。 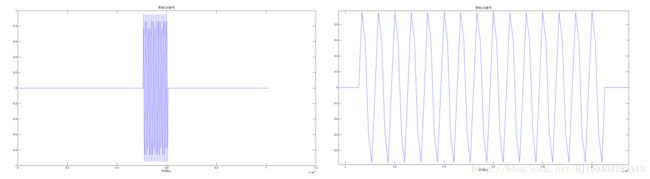
下图展示的是CW信号经FFT变换后形成的幅度谱。 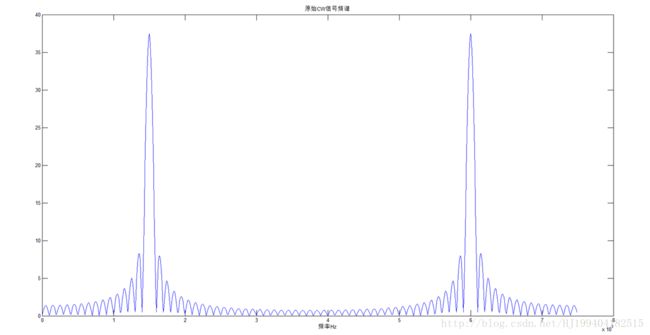
下图展示的是内插了D-1=19个0后的时域波形,右边为放大后的细节图。 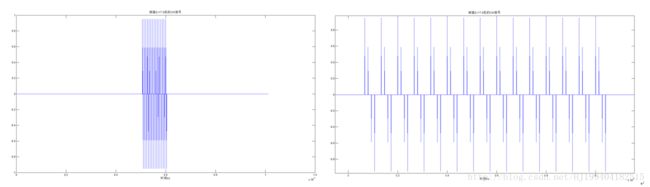
下图展示的是内插D-1=19个0后的频域图,可见采样信号在整个模拟域其频谱是不变的,但是其在对应的频率归一化后的数字域的频谱发生了变化,即有用的信号的频谱宽度变窄了,变为了原来的1/D。 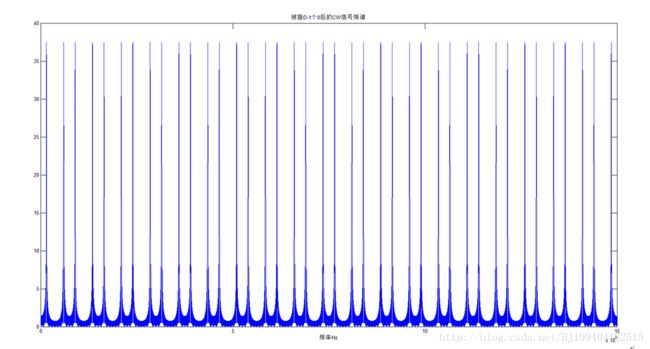
下图展示的是内插了D-1=19个0后的信号经过一个64阶的低通FIR滤波器(截止频率为200KHz)后输出的时域波形,右边的是放大后的细节图。 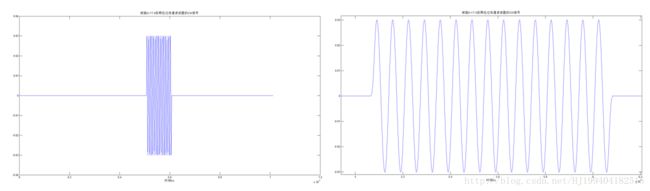
下图展示的是内插了D-1=19个0后的信号经过一个64阶的低通FIR滤波器(截止频率为200KHz)后输出的信号的频域波形,右边的是放大后的细节图。 
下面来改变上采样的倍数,即将程序中的参数D改为40,其它的参数不变。运行程序得到如下一些图形。由于信号在内插之前与上面的一样,因此在此不予再次展示,在此仅展示内插后的一些不同的图形。
下图展示的是内插了D-1=39个0后的时域波形,右边为放大后的细节图。 
下图展示的是内插D-1=39个0后的频域图相比于D=20的情况其数字域的有用的信号的频谱宽度更窄了。 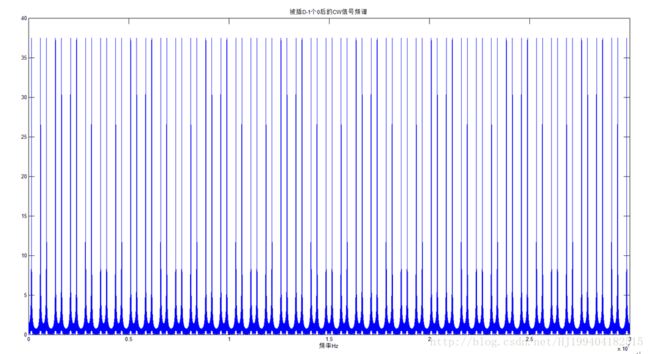
下图展示的是内插了D-1=39个0后的信号经过一个64阶的低通FIR滤波器(截止频率为200KHz)后输出的时域波形,右边的是放大后的细节图。可见滤波的效果不够好。 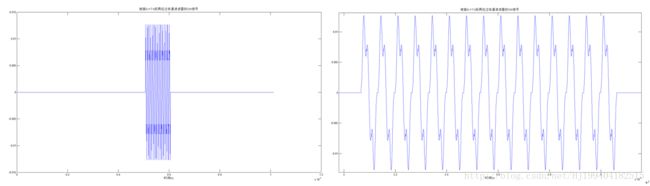
下图展示的是内插了D-1=39个0后的信号经过一个64阶的低通FIR滤波器(截
止频率为200KHz)后输出的信号的频域波形,右边的是放大后的细节图。从频域可以很容易的看出滤波器对其它无用的频谱成分衰减的不够彻底,因此需要提高滤波器的阶数使过渡带更窄,从而将其它无用频谱成分衰减的更彻底。 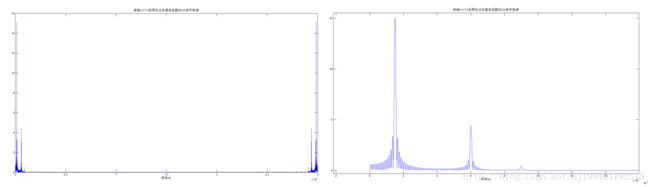
下面按照上面的分析,在D=40的情况下,为了得到更好的内插效果需要将滤波器的阶数提高。因此将程序中的滤波器中的阶数参数N改为128阶,其它的参数不变,得到的内插并经过低通滤波器的图形。
下图展示的是内插了D-1=39个0后的信号经过一个128阶的低通FIR滤波器(截止频率为200KHz)后输出的时域波形,右边的是放大后的细节图。可见滤波的效果比之前的要好很多了。 
下图展示的是内插了D-1=39个0后的信号经过一个128阶的低通FIR滤波器(截止频率为200KHz)后输出的信号的频域波形,右边的是放大后的细节图。从频域可以很容易的看出滤波器比之前的对其它无用的频谱成分衰减更彻底,从而验证了之前的想法。 
小结
通过对CW脉冲信号的内插和滤波分析,可以得到如下结论,随着内插点数的增多,内插后的频谱在模拟域不会发生改变,而在数字域其有用信号的频谱宽度会变窄变为了原来的1/D,因此需要阶数更高的低通滤波器将其滤除,从而更有效的衰减无用信号成分并保留有用信号成分。
内插波束形成的Matlab仿真分析
仿真的流程图为前面的介绍的图(a),即先内插滤波,后波束形成。仿真的信号形式为CW脉冲,频率为150KHz,直线阵,阵元数为64,其它的参数见下面给出的程序。
%内插波束形成
clc;
clear all;
close all;
c = 1500; % 声速 Unit:m/s
f0 = 150e3; % 信号中心频率 Unit:Hz
fs = 5*f0; % 采样率 Unit: /s66.666e3
tao = 0.2e-3; % 信号脉宽 Unit:s
lambda = c/f0; % 波长 Unit:m
d = lambda/2; % 水平方向阵元间距 Unit:m
M = 64; % 阵元数
SNR = 20; % 信噪比 Unit:dB
Detect_dis = 10; % 探测距离 Unit:m
sample_time_Len = 2*Detect_dis/c; %采样总时间
%目标属性
Target_dis = [2 2 2 3 5 7 9 ]; %目标距离接收阵的距离 Unit:m
doppler_v = [0 0 0 0 0 0 0 ]; %相对速度 正数表示靠近 负数表示远离 m/s
theta_a = [60 30 120 61 62 60 100 ]*pi/180; % 方位角
Target_num = length(theta_a); %仿真目标的个数
nTs1 = 0:1/fs:sample_time_Len; %采样时刻(从信号发射算起为0时刻)
sample_points = length(nTs1); %采样点数
%*******************************************************************************************
%生成各个接收换能器通道的采样数据
%*******************************************************************************************
Echo_signal = zeros(sample_points,M);
add_target_num = Target_num;
for i=1:add_target_num %第几个目标1
theta = theta_a(i); %当前目标的水平方位角
tt = 2*Target_dis(i)/c; %计算回波的开始时刻(以左下角的接收换能器为参考,即坐标为(0,0,0))
temp = 10^(-SNR/20);
temp_Echo_signal = zeros(sample_points,M);
d_f = f0*2*doppler_v(i)/c; %计算多普勒频移
f_r = f0 + d_f; %接收的回波信号频率
tao_compressd = tao/(1+2*doppler_v(i)/c); %计算压缩后的脉宽
nTs = 0:1/fs:tao_compressd; %被压缩的回波信号时刻
Echo_points = length(nTs); %被压缩的回波采样点数
for k=1:M
d_x = (k-1)*d*cos(theta); %x轴方向的声程差(相对于坐标原点)
delay = d_x/c; %正数表示超前的时长,负数表示落后的时长
tt_x = tt - delay; %坐标在(x,0,0)位置的接收阵接收到回波的起始时刻
tt_x_num = fix(tt_x*fs)+1; %转换成时刻点
phase = (tt_x_num/fs - tt_x)*f_r*2*pi; %采样认为回波信号开始的时刻与真实的开始时刻相位差
temp_Echo_signal(tt_x_num:(tt_x_num + Echo_points-1),k) = cos(2*pi*f_r*nTs + phase); %对回波信号采样
noise = randn(sample_points,1);
noise = noise * temp;
temp_Echo_signal(:,k) = temp_Echo_signal(:,k) + noise; %加入一定信噪比的噪声
end
Echo_signal = Echo_signal + temp_Echo_signal;
end
clear noise;
clear temp_Echo_signal;
fprintf('信号生成完成\n');
figure;
plot(nTs1,Echo_signal(:,1));
title('回波信号时域波形');
%*******************************************************************************************
%各个通道内插
%*******************************************************************************************
D = 20; %定义上采样倍数
fs_up = fs*D; %上采样率
sample_points_up = sample_points*D; %上采样后的采样点数
nTs_up = (0:sample_points_up-1)/fs_up; %上采样的各个时刻
Echo_signal_up = zeros(sample_points_up,M);
Echo_signal_up(1:D:sample_points_up,:) = Echo_signal;
F_up = (0:sample_points_up-1)*fs_up/sample_points_up;
figure;
plot(nTs_up,Echo_signal_up(:,1));
title('采样点间内插D-1个0后回波信号时域波形');
if add_target_num == 1
figure;
plot(F_up,abs(fft(Echo_signal_up(:,1))));
title('采样点间内插D-1个0后回波信号的频谱');
end
%*******************************************************************************************
%低通滤波
%*******************************************************************************************
N=64; %滤波器的阶数
wc=pi*200e3/(fs*D/2); %截止频率 200KHz
n=0:N-1;
r=(N-1)/2;
hdn = sin(wc*(n-r))/pi./(n-r);
if rem(N,2)~=0
hdn(r+1)=wc/pi;
end
wn = hamming(N); %hamming窗
hn = hdn.*wn';
LPF_Echo_signal_up = filter(hn,1,Echo_signal_up);
figure;
plot(nTs_up,LPF_Echo_signal_up(:,19));
title('采样点间内插D-1个0后回波信号经过数字低通滤波器后的时域波形');
if add_target_num == 1
figure;
plot(F_up,abs(fft(LPF_Echo_signal_up(:,19))));
title('采样点间内插D-1个0后回波信号经过数字低通滤波器后的频谱');
end
%*******************************************************************************************
%时延波束形成
%*******************************************************************************************
tao_min = 1/fs_up; %最小时延
tao_max = d/(lambda*f0); %最大可能的时延
rate = fix(tao_max/tao_min);
beam_angle = acos(((-rate:rate)*tao_min/tao_max))/pi*180; %计算波束角度
Beam_num = rate*2 + 1; %能够形成的最大的波束数目
Beamform_signal = zeros(sample_points,Beam_num);
extend_LPF_Echo_signal_up = zeros(sample_points_up + 2*rate*(M-1),M);
extend_LPF_Echo_signal_up((rate*(M-1)+1):(rate*(M-1)+sample_points_up),:) = LPF_Echo_signal_up;
%按行求和 正中间的波束形成
Beamform_signal(:,rate+1) = sum(extend_LPF_Echo_signal_up((rate*(M-1)+1):D:(rate*(M-1)+sample_points_up),:),2);
for i=1:rate
temp_right = zeros(sample_points,1);
temp_left = zeros(sample_points,1);
for j=1:M
temp = (j-1)*i; %第j个波束的时延个数
temp_right = temp_right + extend_LPF_Echo_signal_up((rate*(M-1)+1-temp):D:(rate*(M-1)+sample_points_up-temp),j);
temp_left = temp_left + extend_LPF_Echo_signal_up((rate*(M-1)+1+temp):D:(rate*(M-1)+sample_points_up+temp),j);
end
Beamform_signal(:,rate+1+i) = temp_right; %右边的
Beamform_signal(:,rate+1-i) = temp_left; %左边的
end
figure;
plot(nTs1,Beamform_signal(:,86),'b',nTs1,Beamform_signal(:,76),'r');
title('第76号波束形成后的时域图形');
figure;
imagesc(nTs1,-rate:rate,abs(Beamform_signal')); %绘制二维时间与水平方位角的回波强度图beam_angle
xlabel('时间s');
ylabel('最小时延个数');下面给出的是运行结果图 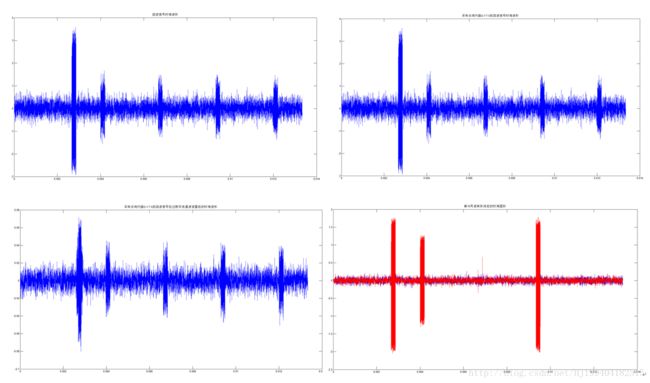
下图是波束形成后的二维图像,横轴代表时间,纵轴代表相邻阵元间的时延所对应的采样点间隔数,程序中采样率是5倍于信号频率,然后上采样20倍,最终能够在0°到180°之间形成101个波束。相邻两个波束的波束角之差不是是一个恒定的值,而是中间的小,两边的大。 
接下来将程序中的D改为40,N改为128,其它的参数不变,运行程序,得到如下的二维图像。此时能够在0°到180°之间形成201个波束。比刚才多了近一倍,由此付出的代价就是需要的计算量更大了。 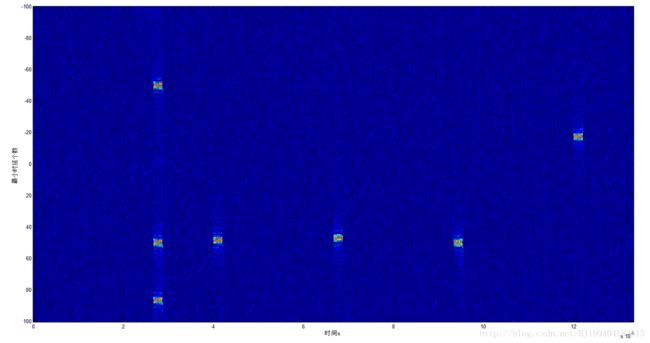
结论
通过前面的仿真分析,可知插的点数越多需要的数字低通滤波器截止频率越低,为了得到更好的滤波效果就需要增大滤波器的阶数,随之而来的计算量也将增大。且进行时延波束形成得到的波束相邻波束之间的波束角差值不是恒定的,即两边的稀疏,中间的密集。如果对于窄带的波束形成,运用相移波束形成,效果要好于内插时延波束形成,因为相移波形形成可以很轻松的将波束控制到想要的角度上,而不用增加额外的计算量,而用内插时延波束形成则很困难,会付出很大的计算代价。