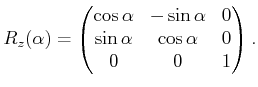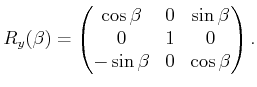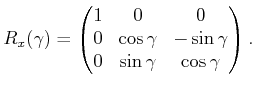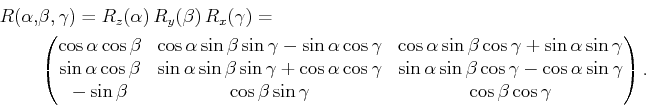- Qt 图形视图框架4-动画、碰撞检测和图形项组
Zy100Papa
Qtc++开发实战qt开发语言
1.动画1.1.使用QObject包装器1.2.属性动画(QPropertyAnimation)1.3.定时器动画(QTimer)1.4.场景推进动画(QGraphicsScene::advance)2.碰撞检测1.动画在Qt图形视图框架中,实现动画效果有多种常用方法,下面介绍几种主要方式:以下是在Qt5.15.5(MinGW环境)中实现图形视图框架动画的常用方法,代码已亲测可正常运行:1.1.使
- Mat转指针和指针转Mat
Ring__Rain
Opencv
Matorigin_Img=Mat::zeros(m_nGoldenHeight,m_nGoldenWidth,CV_8UC1);;uchar*pimage=origin_Img.data;origin_Img.data=pimage;
- 反应式PDF显示:react-pdf入门指南及问题解决方案
卫直超Unity
反应式PDF显示:react-pdf入门指南及问题解决方案react-pdfDisplayPDFsinyourReactappaseasilyasiftheywereimages.项目地址:https://gitcode.com/gh_mirrors/rea/react-pdf项目基础介绍:react-pdf是由CSDN公司开发的InsCodeAI大模型提及的WojciechMaj所创建的一个开源
- Java 导出pdf 写出demo 1、需要设置自定义页眉和文字 2、可以插入表格 3、可以插入图片
赵八斤
java
以下是一个使用iText7库实现PDF导出的Java示例,包含自定义页眉、文字、表格和图片功能:添加Maven依赖com.itextpdfitext7-core7.2.5com.itextpdflayout7.2.5Java示例代码importcom.itextpdf.io.image.ImageDataFactory;importcom.itextpdf.kernel.colors.ColorC
- C# winform利用Graphics绘制数据折线图
int[]x=newint[20];int[]y=newint[20];float[]data=newfloat[20];Point[]pot=newPoint[20];inti=0;Fontf=newFont("隶书",10,FontStyle.Bold);privatevoidForm1_Paint(objectsender,PaintEventArgse){Graphicsgobj=e.Gr
- ReactNative【实战】瀑布流布局列表(含图片自适应、点亮红心动画)
最终效果滚动到最底部实现原理使用绝对定位实现交错衔接图片自适应布局代码范例数据类型typings.d.tstypeArticleSimple={id:number;title:string;userName:string;avatarUrl:string;favoriteCount:number;isFavorite:boolean;image:string;};模拟数据mock/articleL
- 【无标题】导出pdf
JavaPDF导出工具-iText7实现下面是一个使用iText7库实现的PDF导出工具,支持页眉文字和图片、表格插入和图片插入功能。importcom.itextpdf.io.image.ImageData;importcom.itextpdf.io.image.ImageDataFactory;importcom.itextpdf.kernel.colors.ColorConstants;im
- Python淘宝拍立淘按图搜索API接口,json数据示例参考
ID_18007905473
pythonAPI数据库json大数据python
淘宝拍立淘按图搜索API接口示例淘宝的拍立淘(图片搜索)功能通常是通过淘宝开放平台提供的API实现的。以下是一个模拟的JSON数据示例和接口调用参考:模拟API请求示例importrequestsimportbase64#示例图片路径image_path="example.jpg"#读取图片并编码为base64withopen(image_path,"rb")asimage_file:encode
- JavaWeb三大组件啊-Filter
sleepcattt
filterjava
一、Filter过滤器简介过滤器可以对访问的静态资源和动态资源进行过滤,既可以过滤请求,也可以过滤响应1.应用场景列举统一编码处理登入验证敏感字符过滤![[Pastedimage20250422121326.png]]相当于在Client和Server之间创建了一个中间层Filter,先经过Filter再到Server2.使用先创建实现类,来实现javax.servlet.Filter包的接口,实
- pytest中测试特定接口
qq_47150350
pytest服务器运维
在pytest中只测试特定接口有以下几种常用方法:1.通过测试函数名精确匹配直接指定测试文件和函数名:pytesttest_api.py::test_upload_image_with_library这将只运行test_api.py文件中名为test_upload_image_with_library的测试函数。2.使用关键字匹配(-k参数)通过函数名中的关键字筛选测试:pytesttest_ap
- Docker快速单点部署Elasticsearch
❀͜͡傀儡师
dockerelasticsearch
x86架构dockerpullregistry.cn-hangzhou.aliyuncs.com/qiluo-images/elasticsearch:8.17.4arm架构dockerpullregistry.cn-hangzhou.aliyuncs.com/qiluo-images/linux_arm64_elasticsearch:8.17.43、elasticsearch安装mkdir-p
- Docker从0到1:入门指南
宇航AI
docker容器运维
目录什么是DockerDocker的核心概念容器(Container)镜像(Image)镜像层(ImageLayers)Dockerfile仓库(Repository)数据卷(Volume)网络(Network)Docker架构Docker安装Docker基本命令实际应用场景Docker生态系统最佳实践常见问题什么是DockerDocker是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依
- OpenGL ES 面试高频知识点
字节流动
OpenGLES3.0面试OpenGLES音视频图形渲染c++Android
OpenGL共享上下文使用场景?有哪些资源可以共享?多线程渲染或者跨窗口渲染,共享上下文可以使得多个线程、窗口之间能够共享OpenGL对象(如纹理、shader等)和状态信息,避免了在多个上下文之间频繁地进行数据拷贝和同步操作,减少资源消耗,提高性能。可以共享的资源:纹理;shader;program着色器程序;buffer类对象,如VBO、EBO、RBO等。不可以共享的资源:FBO帧缓冲区对象(
- Docker 学习入门篇:从基础概念到实战部署
一、Docker核心概念与核心价值1.1Docker是什么?Docker是基于Go语言开发的开源容器化平台,旨在实现“一次镜像,处处运行”。它通过将应用程序及其依赖环境(代码、运行时、系统工具、系统库等)打包成一个轻量级、可移植的镜像(Image),使应用能够在不同环境中稳定运行,彻底解决了传统开发中环境不一致、部署复杂的难题。1.2Docker解决了什么问题?环境一致性难题:开发、测试、生产环境
- Cesium billboard 实现动态效果
swift1224L
Cesium前端开发语言webgl
Cesiumbillboard实现动态效果自转、跳动、闪烁、旋转等动态效果加载GIF自转、跳动、闪烁、旋转等动态效果/***利用BillboardGraphics的scale、rotation、width、position属性和和CallbackProperty实现动态改变entitybillboard*/loadDynamicBillboardByEntity(viewer:Cesium.Vie
- ReactNative【实战系列教程】我的小红书 3 -- 自定义底栏Tab导航(含图片选择 expo-image-picker 的使用)
最终效果技术要点自定义tab需从“expo-router/ui”中导入TabList,Tabs,TabSlot,TabTrigger实现Tabs表示含底栏的页面容器TabList为整个底栏的容器TabSlot渲染tab路由对应的页面TabTrigger触发tab底栏的路由导航name属性对应页面文件href属性对应页面的路由import{Tabs,TabList,TabTrigger,TabSlo
- 图像哈希:DCT篇
怪味&先森
科研篇:图像哈希哈希算法opencv计算机视觉
RobustimagehashingwithdominantDCTcoefficients文章信息作者:唐振军期刊:Optic(Q2/3区)题目:RobustimagehashingwithdominantDCTcoefficients目的、实验步骤及结论目的:使用传统的DCT对图像进行压缩,由于压缩后的信息主要集中在左上角,因此使用左上角的数据进行比较生成图像的哈希值。实验步骤数据预处理:双线性
- ReactNative图片自适应高度
吴佩佩佩佩
ReactNative安卓reactnativeandroid
importReact,{useState,useEffect}from'react';import{Image}from'react-native';exportdefault({source={},style={},width=0})=>{const[height,setHeight]=useState(100);useEffect(()=>{if(source.uri){//网络图Image
- Pod调度、嵌入式脚本、Pod标签管理
yanjiaweiya
云原生kubernetes容器
多容器Pod案例3排错[root@master~]#vimweb2.yaml---kind:PodapiVersion:v1metadata:name:web2namespace:defaultspec:containers:-name:nginximage:myos:nginx-name:apacheimage:myos:httpdstatus:{}[root@master~]#kubectla
- ERROR: failed to solve: failed to read dockerfile: open Dockerfile: no such file or directory
Upper999
Docker运维linuxdocker
1通过Dockerfile方式,生成镜像时报错(如下)[zxx@192~]$dockerbuild-tmy_first_build_image.[+]Building0.1s(1/1)FINISHEDdocker:default=>[internal]loadbuilddefinitionfromDockerfile0.0s=>=>transferringdockerfile:2B0.0sERRO
- Docker 将镜像打成压缩包将压缩包传到服务器运行
一只帆記
Dockerdocker服务器容器
1.本地操作:将镜像打包为压缩文件#查看本地镜像列表dockerimages#打包指定镜像(替换your_image:tag为实际镜像名称和标签)dockersaveyour_image:tag|gzip>my_image.tar.gz示例:dockersavenginx:latest|gzip>nginx.tar.gz2.传输压缩包到服务器使用scp命令传输(确保服务器已开启SSH):scpmy
- Docker相关内容
牧天白衣.
Dockerdockereureka容器
自己打包的Docker镜像,如何拉取到服务器使用1.通过Docker保存和加载镜像你可以将本地镜像保存为.tar文件,然后将其传输到目标服务器,并使用dockerload命令加载该镜像。1.1在本地机器上保存镜像首先,在本地机器上使用dockersave命令将镜像保存为.tar文件:dockersave-omy_image.tarmy_image_name:tagmy_image_name:tag
- 尝试加载 Oracle 客户端库时引发 BadImageFormatException,如果在安装32位Oracle 客户端组件的情况下64位模式运行,将出现此问题
尊治
自动化oracle数据库sql
1.错误发生的时的情况电脑软件配置:WIN10(64位)、Oracle12c(64位)、PLSQLDeveloper(64位),VS2019用VS2019工具栏里的连接到数据库功能连接Oracle时报错误,错误内容:尝试加载Oracle客户端库时引发BadImageFormatException,如果在安装32位Oracle客户端组件的情况下64位模式运行,将出现此问题根本原因:基本都是软件访问调
- docker 常用命令
docker1.docker镜像下载dockerpullnginx//下载nginx镜像dockerimages//列出常用镜像dockerrmi镜像(image)的ID//移除镜像2.运行容器dockerrun容器名字dockerrun-d容器名字//容器在后台运行,容器的日志不会打印在控制台dockerrun-p80:80nginx//运行镜像中的实例,因为本机的端口实际上是不含镜像的,通过
- python垃圾回收机制_python3
2401_84585372
程序员python开发语言
1、变量名与值内存地址的关联关系存放于栈区2、变量值存放于堆区,内存管理回收的则是堆区的内容,定义了两个变量x=10、y=20,详解如下图:功能:计算灰度值分布。算子gray_histo为区域内的图像计算灰度值的绝对和相对的直方图。两个直方图都是256个值的元组,它们从0开始,包含图像的各个灰度值的频率。输入参数:Regions:输入计算的区域;Image:输入图像(byte/cyclic/direction/intl/
- 【LeetCode 热题 100】48. 旋转图像——转置+水平翻转
xumistore
LeetCodeleetcode算法职场和发展java
Problem:48.旋转图像题目:给定一个n×n的二维矩阵matrix表示一个图像。请你将图像顺时针旋转90度。你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。文章目录整体思路完整代码时空复杂度时间复杂度:O(N^2)空间复杂度:O(1)整体思路这段代码旨在解决一个经典的矩阵问题:旋转图像(RotateImage)。问题要求将一个NxN的二维矩阵顺时针
- HTML5中背景图片如何设置
十指流玉
HTML
自己试验了很多种方式,最终发现有一种方式最得朕心~~哈哈哈哈哈先看一下效果图吧:只截取了一部分,图片的人物不会因为页面大小而变得扭曲(这一点非常重要),我已经很满足啦~~~~~下面看一下代码吧,其实也很简单。body{/*background:rgb(185,246,246);*//*设置颜色背景*/background-image:url(photo5.png);/*设置背景图片*/backgr
- VTK中使用梯度幅值计算边缘
点PY
三维渲染服务器前端linux
#include#includevtkSmartPointerDetectEdgesWithGradient(vtkImageData*binaryVolume){</
- html2Canvas不支持object-fit属性导致图片变形了
懒大王、
前端css3
html2Canvas是不支持object-fit属性data(){return{leftImageStyle:{position:'absolute',width:'1952px',height:'3600px',left:'0',top:'0'}};},mounted(){this.$nextTick(()=>{this.calculateImageDimensions();});},calc
- java短路运算符和逻辑运算符的区别
3213213333332132
java基础
/*
* 逻辑运算符——不论是什么条件都要执行左右两边代码
* 短路运算符——我认为在底层就是利用物理电路的“并联”和“串联”实现的
* 原理很简单,并联电路代表短路或(||),串联电路代表短路与(&&)。
*
* 并联电路两个开关只要有一个开关闭合,电路就会通。
* 类似于短路或(||),只要有其中一个为true(开关闭合)是
- Java异常那些不得不说的事
白糖_
javaexception
一、在finally块中做数据回收操作
比如数据库连接都是很宝贵的,所以最好在finally中关闭连接。
JDBCAgent jdbc = new JDBCAgent();
try{
jdbc.excute("select * from ctp_log");
}catch(SQLException e){
...
}finally{
jdbc.close();
- utf-8与utf-8(无BOM)的区别
dcj3sjt126com
PHP
BOM——Byte Order Mark,就是字节序标记 在UCS 编码中有一个叫做"ZERO WIDTH NO-BREAK SPACE"的字符,它的编码是FEFF。而FFFE在UCS中是不存在的字符,所以不应该出现在实际传输中。UCS规范建议我们在传输字节流前,先传输 字符"ZERO WIDTH NO-BREAK SPACE"。这样如
- JAVA Annotation之定义篇
周凡杨
java注解annotation入门注释
Annotation: 译为注释或注解
An annotation, in the Java computer programming language, is a form of syntactic metadata that can be added to Java source code. Classes, methods, variables, pa
- tomcat的多域名、虚拟主机配置
g21121
tomcat
众所周知apache可以配置多域名和虚拟主机,而且配置起来比较简单,但是项目用到的是tomcat,配来配去总是不成功。查了些资料才总算可以,下面就跟大家分享下经验。
很多朋友搜索的内容基本是告诉我们这么配置:
在Engine标签下增面积Host标签,如下:
<Host name="www.site1.com" appBase="webapps"
- Linux SSH 错误解析(Capistrano 的cap 访问错误 Permission )
510888780
linuxcapistrano
1.ssh -v
[email protected] 出现
Permission denied (publickey,gssapi-keyex,gssapi-with-mic,password).
错误
运行状况如下:
OpenSSH_5.3p1, OpenSSL 1.0.1e-fips 11 Feb 2013
debug1: Reading configuratio
- log4j的用法
Harry642
javalog4j
一、前言: log4j 是一个开放源码项目,是广泛使用的以Java编写的日志记录包。由于log4j出色的表现, 当时在log4j完成时,log4j开发组织曾建议sun在jdk1.4中用log4j取代jdk1.4 的日志工具类,但当时jdk1.4已接近完成,所以sun拒绝使用log4j,当在java开发中
- mysql、sqlserver、oracle分页,java分页统一接口实现
aijuans
oraclejave
定义:pageStart 起始页,pageEnd 终止页,pageSize页面容量
oracle分页:
select * from ( select mytable.*,rownum num from (实际传的SQL) where rownum<=pageEnd) where num>=pageStart
sqlServer分页:
- Hessian 简单例子
antlove
javaWebservicehessian
hello.hessian.MyCar.java
package hessian.pojo;
import java.io.Serializable;
public class MyCar implements Serializable {
private static final long serialVersionUID = 473690540190845543
- 数据库对象的同义词和序列
百合不是茶
sql序列同义词ORACLE权限
回顾简单的数据库权限等命令;
解锁用户和锁定用户
alter user scott account lock/unlock;
//system下查看系统中的用户
select * dba_users;
//创建用户名和密码
create user wj identified by wj;
identified by
//授予连接权和建表权
grant connect to
- 使用Powermock和mockito测试静态方法
bijian1013
持续集成单元测试mockitoPowermock
实例:
package com.bijian.study;
import static org.junit.Assert.assertEquals;
import java.io.IOException;
import org.junit.Before;
import org.junit.Test;
import or
- 精通Oracle10编程SQL(6)访问ORACLE
bijian1013
oracle数据库plsql
/*
*访问ORACLE
*/
--检索单行数据
--使用标量变量接收数据
DECLARE
v_ename emp.ename%TYPE;
v_sal emp.sal%TYPE;
BEGIN
select ename,sal into v_ename,v_sal
from emp where empno=&no;
dbms_output.pu
- 【Nginx四】Nginx作为HTTP负载均衡服务器
bit1129
nginx
Nginx的另一个常用的功能是作为负载均衡服务器。一个典型的web应用系统,通过负载均衡服务器,可以使得应用有多台后端服务器来响应客户端的请求。一个应用配置多台后端服务器,可以带来很多好处:
负载均衡的好处
增加可用资源
增加吞吐量
加快响应速度,降低延时
出错的重试验机制
Nginx主要支持三种均衡算法:
round-robin
l
- jquery-validation备忘
白糖_
jquerycssF#Firebug
留点学习jquery validation总结的代码:
function checkForm(){
validator = $("#commentForm").validate({// #formId为需要进行验证的表单ID
errorElement :"span",// 使用"div"标签标记错误, 默认:&
- solr限制admin界面访问(端口限制和http授权限制)
ronin47
限定Ip访问
solr的管理界面可以帮助我们做很多事情,但是把solr程序放到公网之后就要限制对admin的访问了。
可以通过tomcat的http基本授权来做限制,也可以通过iptables防火墙来限制。
我们先看如何通过tomcat配置http授权限制。
第一步: 在tomcat的conf/tomcat-users.xml文件中添加管理用户,比如:
<userusername="ad
- 多线程-用JAVA写一个多线程程序,写四个线程,其中二个对一个变量加1,另外二个对一个变量减1
bylijinnan
java多线程
public class IncDecThread {
private int j=10;
/*
* 题目:用JAVA写一个多线程程序,写四个线程,其中二个对一个变量加1,另外二个对一个变量减1
* 两个问题:
* 1、线程同步--synchronized
* 2、线程之间如何共享同一个j变量--内部类
*/
public static
- 买房历程
cfyme
2015-06-21: 万科未来城,看房子
2015-06-26: 办理贷款手续,贷款73万,贷款利率5.65=5.3675
2015-06-27: 房子首付,签完合同
2015-06-28,央行宣布降息 0.25,就2天的时间差啊,没赶上。
首付,老婆找他的小姐妹接了5万,另外几个朋友借了1-
- [军事与科技]制造大型太空战舰的前奏
comsci
制造
天气热了........空调和电扇要准备好..........
最近,世界形势日趋复杂化,战争的阴影开始覆盖全世界..........
所以,我们不得不关
- dateformat
dai_lm
DateFormat
"Symbol Meaning Presentation Ex."
"------ ------- ------------ ----"
"G era designator (Text) AD"
"y year
- Hadoop如何实现关联计算
datamachine
mapreducehadoop关联计算
选择Hadoop,低成本和高扩展性是主要原因,但但它的开发效率实在无法让人满意。
以关联计算为例。
假设:HDFS上有2个文件,分别是客户信息和订单信息,customerID是它们之间的关联字段。如何进行关联计算,以便将客户名称添加到订单列表中?
&nbs
- 用户模型中修改用户信息时,密码是如何处理的
dcj3sjt126com
yii
当我添加或修改用户记录的时候对于处理确认密码我遇到了一些麻烦,所有我想分享一下我是怎么处理的。
场景是使用的基本的那些(系统自带),你需要有一个数据表(user)并且表中有一个密码字段(password),它使用 sha1、md5或其他加密方式加密用户密码。
面是它的工作流程: 当创建用户的时候密码需要加密并且保存,但当修改用户记录时如果使用同样的场景我们最终就会把用户加密过的密码再次加密,这
- 中文 iOS/Mac 开发博客列表
dcj3sjt126com
Blog
本博客列表会不断更新维护,如果有推荐的博客,请到此处提交博客信息。
本博客列表涉及的文章内容支持 定制化Google搜索,特别感谢 JeOam 提供并帮助更新。
本博客列表也提供同步更新的OPML文件(下载OPML文件),可供导入到例如feedly等第三方定阅工具中,特别感谢 lcepy 提供自动转换脚本。这里有导入教程。
- js去除空格,去除左右两端的空格
蕃薯耀
去除左右两端的空格js去掉所有空格js去除空格
js去除空格,去除左右两端的空格
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>&g
- SpringMVC4零配置--web.xml
hanqunfeng
springmvc4
servlet3.0+规范后,允许servlet,filter,listener不必声明在web.xml中,而是以硬编码的方式存在,实现容器的零配置。
ServletContainerInitializer:启动容器时负责加载相关配置
package javax.servlet;
import java.util.Set;
public interface ServletContainer
- 《开源框架那些事儿21》:巧借力与借巧力
j2eetop
框架UI
同样做前端UI,为什么有人花了一点力气,就可以做好?而有的人费尽全力,仍然错误百出?我们可以先看看几个故事。
故事1:巧借力,乌鸦也可以吃核桃
有一个盛产核桃的村子,每年秋末冬初,成群的乌鸦总会来到这里,到果园里捡拾那些被果农们遗落的核桃。
核桃仁虽然美味,但是外壳那么坚硬,乌鸦怎么才能吃到呢?原来乌鸦先把核桃叼起,然后飞到高高的树枝上,再将核桃摔下去,核桃落到坚硬的地面上,被撞破了,于是,
- JQuery EasyUI 验证扩展
可怜的猫
jqueryeasyui验证
最近项目中用到了前端框架-- EasyUI,在做校验的时候会涉及到很多需要自定义的内容,现把常用的验证方式总结出来,留待后用。
以下内容只需要在公用js中添加即可。
使用类似于如下:
<input class="easyui-textbox" name="mobile" id="mobile&
- 架构师之httpurlconnection----------读取和发送(流读取效率通用类)
nannan408
1.前言.
如题.
2.代码.
/*
* Copyright (c) 2015, S.F. Express Inc. All rights reserved.
*/
package com.test.test.test.send;
import java.io.IOException;
import java.io.InputStream
- Jquery性能优化
r361251
JavaScriptjquery
一、注意定义jQuery变量的时候添加var关键字
这个不仅仅是jQuery,所有javascript开发过程中,都需要注意,请一定不要定义成如下:
$loading = $('#loading'); //这个是全局定义,不知道哪里位置倒霉引用了相同的变量名,就会郁闷至死的
二、请使用一个var来定义变量
如果你使用多个变量的话,请如下方式定义:
. 代码如下:
var page
- 在eclipse项目中使用maven管理依赖
tjj006
eclipsemaven
概览:
如何导入maven项目至eclipse中
建立自有Maven Java类库服务器
建立符合maven代码库标准的自定义类库
Maven在管理Java类库方面有巨大的优势,像白衣所说就是非常“环保”。
我们平时用IDE开发都是把所需要的类库一股脑的全丢到项目目录下,然后全部添加到ide的构建路径中,如果用了SVN/CVS,这样会很容易就 把
- 中国天气网省市级联页面
x125858805
级联
1、页面及级联js
<%@ page language="java" import="java.util.*" pageEncoding="UTF-8"%>
<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN">
&l
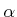 about the
about the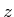 -axis. The rotation matrix is given by
-axis. The rotation matrix is given by
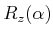 form a 2D rotationapplied to the
form a 2D rotationapplied to the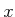 and
and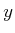 coordinates, whereas the
coordinates, whereas the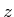 coordinateremains constant.
coordinateremains constant. 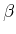 about the
about the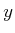 -axis. The rotation matrix is givenby
-axis. The rotation matrix is givenby
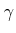 about the
about the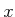 -axis. The rotation matrix is given by
-axis. The rotation matrix is given by