今天是2020年1月29日星期三,疫情又严重了许多。得知假期延长,心中自是无限欢喜,冗长的假期和在校的时间一样无趣,怎么打发时间呢?另外,25岁开始了,如何让生活繁忙起来,让30岁有所收获,这个问题也一直困扰自己。
不想空度这个假期,更不想空度接下来读研的生活。把谷歌上收藏的书签整理了一遍,重新找出这本读了三分之一的《统计学习方法》,以及众多大佬的博客,那就用2020这年写写博客吧,算是找点事情做,完成好久之前的这个想法。现在查资料这么方便,有各位大佬指导,汇总汇总文字还是比较容易做到的,加油~坚持下去~
在这里阐述下写博客的初心,读李航老师的统计学习方法,受益匪浅,知识点甚多,不能及时笔记,总是浅尝辄止。好像哪个知识点都看到了,又好像什么知识点都没有深入,复述的时候,脑子里空白,没有东西。在这里,力图把每个知识点搞透彻,写出来。网上资料非常丰富,深入也好,浅析也罢,都不是自己的,只有自己整理出来,才算是学到了。
GitHub:https://github.com/wangzycloud/statistical-learning-method
感知机算法
引入
最初接触感知机是在神经网络的神经元部分。感知机是二分类的线性分类模型,输入是单个实例的特征向量,输出为实例的类别。举个例子:流感病人是否要进行输液,病人具有1)发热 2)咳嗽 3)乏力4)打喷嚏症状,四个症状组成四维特征向量,每个分量值属于不同区间。医生会根据病人各个症状的强弱表现,判断病人是否需要输液。感知机算法属于判别模型,旨在找出对于输入空间将实例划分为正负两类的分离超平面,也就是例子中找到判断病人是否需要输液的界限。
在这里,医生往往根据经验去判断病人的发热情况,若体温达到39.9°,这是必然要输液了;若体温不太高,其它症状明显,则有输液的可能(仅为举例);若体温正常,其它症状不明显,则吃药就会治愈了,不需要输液。计算机面对这个问题,如何进行判断呢?医生有薪火相传的经验和大量学习到的知识作为判断依据,计算机如何做到呢?
我们有大量的数据,现在提到的感知机算法,旨在通过训练数据,学习病人是否进行输液的这个界限。“学习”是通过执行某个过程不断改变自身性能的过程,什么是衡量性能的指标?如何进行性能提升?接下来将按照书中的章节,从学生的角度记录感知机模型、学习策略、损失函数、学习算法、对偶形式以及收敛性。
感知机模型
这是感知机模型的精确定义,以病人是否需要输液作为例子,输入x表示一个病人的特征向量,如(39.9°,是,是,是)T,表示体温39.9°,有咳嗽症状,乏力并且打喷嚏。输出y表示该病人是否需要输液。为了得到输入空间到输出空间的映射关系,通过符号函数(sign(x))来对特征向量与参数向量内积值进行判断,值若大于等于0,即位于界限上方,则为正例需要输液。
该例中,输入空间特征向量为四维向量,不容易进行学习,结合书中几何解释。将病人的四维特征向量更改为二维向量:(体温,其它症状程度)T,其它症状程度区间为[0,5],例(39.9,5)T表示体温39.9°其它症状非常明显。
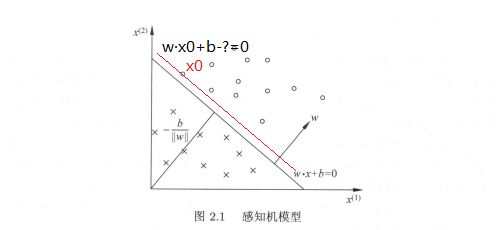
首先理解分离超平面这个概念。超平面可以理解为比当前维度低一维的几何表示,比如在二维空间里,超平面是一条线;三维空间里是一个平面;四维及四维以上就没法用几何表示,但统称为“超平面”。通过分离超平面,将当前维度空间划分为两个部分,如图2.1,在二维空间上,分离超平面是线性方程w·x+b=0,将坐标系分为了右上、左下两个部分。
在这里,我们可以将坐标轴x(1)理解为特征向量中的分量一:体温,坐标轴x(2)理解为分量二:其它症状程度。感知机模型通过大量数据,学习到一组合适的w,b,即模型参数,该参数可以构建完美的划分两个部分的分离超平面。在该特征向量为二维向量的例子中,就是学习到合适的斜率和截距,得到的分离超平面(直线)可以准确的将所有数据划分到两个部分,对于新的输入实例可以划分到所属的区域,得到类别。在病人是否需要输液的例子中,图2.1右上部分圆圈可以理解为为正例,判断为需要输液。
感知机学习策略
感知机学习策略以数据集具有线性可分性作为前提,即给定一个数据集,存在某个超平面S能够将数据集的正实例点和负实例点完全正确的划分到超平面的两侧。感知机的学习目标是求得一个能够将线性可分数据集正负实例点正确分开的分离超平面,也就是确定感知机的模型参数w,b,因此需要确定一个合适的损失函数,并将其最小化。
书中对损失函数的选择有两种思路,第一种很自然的思路是选择误分类点的总数,优化的反向朝着误分类点总数减少的方向,每次移动超平面,使移动后的超平面能够自然的减少误分类点的总数。但是,误分类点总数不是模型参数w,b的连续可导函数,就是说找不到一种自变量w,b变化与因变量误分类点总数的连续可导映射关系,不利于最优化求解。
因此,如何选择合适的映射关系,自变量w,b变化(超平面移动),函数具备连续可导的条件,可以通过最优化进行求解。第二种思路是误分类点到超平面S的总距离。
初次看到这个公式的时候,并没能够深入理解“距离”这个概念。再次翻看图2.1感知机模型,注意到,作为超平面的线性方程w·x+b=0,其中的w和x要从向量的角度理解,即向量x由(x(1),x(2))两个分量构成,则w同样是两个分量的参数向量,并且w为该分离超平面的法向量。以该分离超平面的模型参数w,b作为基准,任一点x0由公式w·x0+b=?,得到值?,实际上,可以将w·x0+b-?=0视作平移的超平面。
平移的值|?|作为x0到超平面S的距离值。在这里,简单叙述一下对公式中分母||w||的理解。学习过SVM的同学会知道几何间隔和函数间隔的概念,公式除以||w||即为几何间隔,表示几何距离。求所有误分类点的距离和,也就是求|wx+b|的总和,让它最小化。有一种思路,把w和b等比例缩小,比如说w改为0.5w,b改为0.5b,线还是那条线,但是值缩小两倍,可以接着缩!缩到0去!这样的最小化,没有太大的意义。所以,我们要加点约束,让整个式子除以w的模长。啥意思?就是w不管怎么样,要除以它的单位长度。如果把w和b等比例缩小,那||w||也会等比例缩小,平移的相对距离值仍然不变。举个地图比例尺的例子,几何距离好比是A、B两个地点地面上测量的实际距离值,在不同比例尺的地图上,比例尺越大1:10,实际距离的100米,在地图上显示的距离长;比例尺越小1:100,实际距离的100米,在地图上显示的距离短。无论A、B两个地点在地图上的相距多远(比例尺不同),物理上实际的距离是不会变的,所有的地图距离除以比例尺就好了,得到实际距离。只要大家使用同一个比例尺,就可以用地图上的距离表示实际的距离,且不会出错。
对于误分类的点来说,上述第一个公式,总是正确的。w·xi+b大于0时,yi=1(理应),判断为yi=-1(判断出错),则-yi(w·xi+b)>0,反之亦然。因此,误分类点xi到超平面的距离S为第二个公式。
公式最后不考虑除以模长,变成了函数间隔,为什么可以这么做呢?不考虑wb等比例缩小这件事了吗?有一种解释是这样说的:感知机是误分类驱动的算法,它的终极目标是没有误分类的点,如果没有误分类的点,总和距离就变成了0,w和b值怎样都没用。所以几何间隔和函数间隔在感知机的应用上没有差别,为了计算简单,使用函数间隔。
我们可以明确的知道,该损失函数是非负的,如果没有误分类点,损失函数值为0,并且误分类点越少,误分类点距离分离超平面越近,损失函数的值越小。我们可以理解为:对于一个特定的样本点,被分类错误时,该点到分离超平面的距离是该超平面参数w,b的线性函数;被正确分类时,为0。我们把训练集中的所有误分类点距离超平面的总和,作为超平面w,b的连续可导函数。
感知机的学习策略就是从假设空间中求得使公式2.4损失函数最小时的模型参数w,b。
感知机学习算法
通过感知机策略的制定,感知机学习问题转化为求解损失函数的最优化问题,选择的方法是梯度下降法。首先学习的是感知机学习算法的原始形式。
公式2.5极小化问题可以理解为找到使所有误分类点距离超平面最小时的模型参数w,b,即确定一个可以将正负类划分开的分离超平面,使得损失函数值最小。
在该算法原始形式的思路中,首先任意选取一个超平面w0,b0,然后用梯度下降方法不断的极小化目标函数2.5,在该算法中要注意一个问题,书中解释了极小化过程并不是一次使M中所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降。简单来说,就是采用了随机梯度下降的方式(具体知识可以见接下来的神经网络部分)。
梯度首先是一个向量,方向反映的是函数值增长最快的方向,值的大小反映的是增长幅度,通过求解损失函数的偏导数得到。在上述四个公式中,可以看到前两个公式中梯度是由损失函数2.5求解偏导数求得。在算法的执行过程中,是应用随机梯度下降思想,采用公式2.6和2.7对参数值进行修改,以参数w更新的公式2.6为例,η为学习率,表示参数w更新的步长,也就是梯度值更新多少。在函数极小化的过程中,为了找到极小值时的参数值w,对当前参数值w0,减去函数值增长最快方向处的值,w0-(-ηyixi)=w0+ηyixi。
可以直观的看出,当一个实例点被错误分类时,也就是位于分离超平面错误的一侧,需要调整w,b的值(调整的方向是使损失函数值变小的方向),使分离超平面变动,以减小该误分类点到该超平面的距离,直到超平面越过该误分类点使其被正确分类。具体算法如下:
流程图示:
算法的收敛性
该部分内容,开学后手写整理。
感知机算法的对偶形式
对偶形式的基本想法是,将w和b表示为实例xi和标记yi的线性组合的形式,通过求解其系数而求得w和b。
关于对偶形式,上述描述精炼的解释了该思路的内含。首先对偶是从一个不同的角度去解答相似的问题,问题的解是相通的。或者说原始问题求解复杂,我们通过求解一个相对简单的问题得到原始问题的解。
在感知机算法的原始形式中,我们通过极小化损失函数,得到了参数w,b的更新公式:
该参数更新公式指明了原始形式中,参数的迭代更新会使得误分类点距离分离超平面越来越近,实际是分离超平面变动,使误分类点能够正确分类(也就是朝着损失函数减小的方向变动)。在对偶形式中,对该更新公式进行考量,假设初始值w0,b0均为0,误分类点(xi,yi)通过参数更新公式,逐步修改w,b,设修改n次可以得到分离超平面,那么,我们可以有以下新的更新公式:
公式2.14和公式2.15反映了新的参数更新过程,有了现在新的更新过程,我们还看不到对偶问题简单在了哪里,好像只是对迭代公式赋初值零时候的特殊情况分析。有必要对分析进行强调,实例点更新次数越多,也就意味着该实例点距离分离超平面越近,也就越难被正确分类,就是说这样的实例点对学习结果的影响较大,类似于SVM中的支持向量。
学习到这里,感觉书本上的对偶形式算法,不太清晰的说明内容,稍后粘贴知乎大佬的高赞回答,一千个读者一千个哈姆雷特,什么方式能更好理解,就采用什么答案吧。
从新感知机模型中可以看到,对偶形式中训练实例仅以内积的形式出现,为了方便运算,可以预先将训练实例间的内积计算出来并以矩阵的形式存储。结合新的参数更新公式,我们可以发现,对偶形式的基本想法是将w和b表示为实例xi和标记yi的线性组合的形式,通过求解其系数而求得w和b。在这里,我们看一下知乎高赞回答:
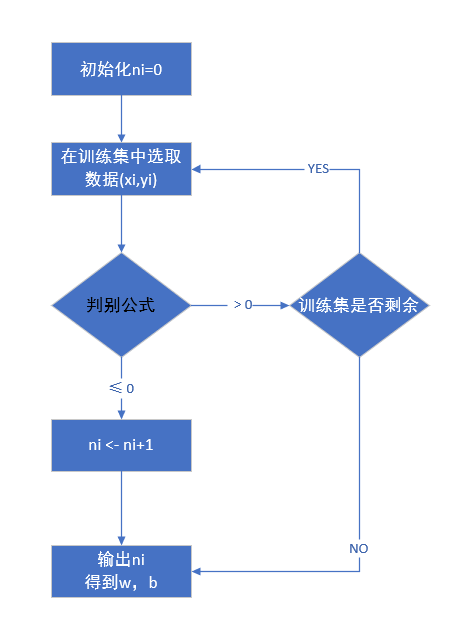
在该回答中,可以明显的看出原始形式和对偶形式在形式上的差别,由于参数更新公式的改变,学习的目标不再是w和b,而是更新次数ni,并且,判别公式中出现了实例点的内积形式。在训练过程中,可以通过事先计算好所有的内积,从而加快训练过程。
流程图示:
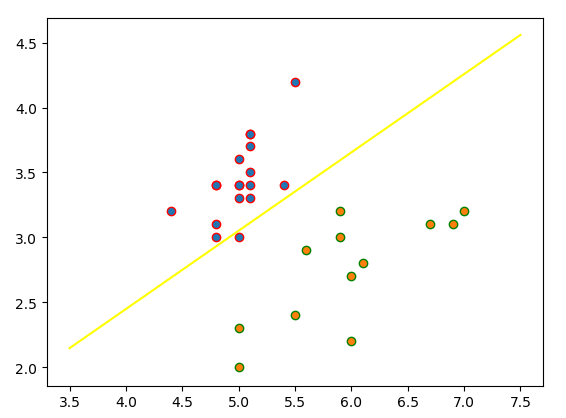
代码效果