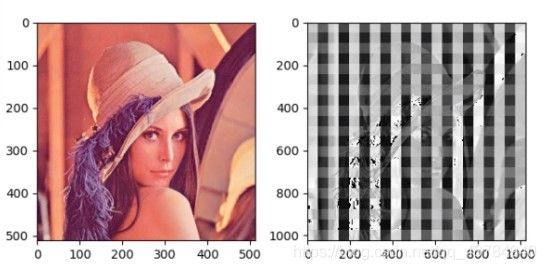
【学习笔记】Pytorch深度学习-网络层之卷积层
Pytorch深度学习-网络层之卷积层
- 卷积概念
- Pytorch中卷积实现—nn.Conv2d()
- Pytorch中转置卷积—nn.ConvTranspose
卷积概念
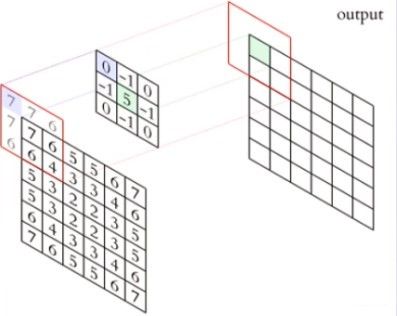
卷积运算:卷积核在输入信号(图像)上滑动,相应位置上进行先乘后加的运算
以上图为例,中间为卷积核,在输入图像上进行滑动,当滑动到当前位置时,其卷积运算操作是对卷积核所覆盖像素,进行权值和对应位置处像素的乘加:
o u t p u t = ( 7 ∗ 0 + 7 ∗ ( − 1 ) + 6 ∗ 0 + 7 ∗ ( − 1 ) + 7 ∗ 5 + 6 ∗ ( − 1 ) + 6 ∗ 0 + 6 ∗ ( − 1 ) + 4 ∗ 0 ) \ output= (7*0+7*(-1)+6*0+7*(-1)+7*5+6*(-1)+6*0+6*(-1)+4*0) output=(7∗0+7∗(−1)+6∗0+7∗(−1)+7∗5+6∗(−1)+6∗0+6∗(−1)+4∗0)
这样才输出作为feature map特征图中的1个像素点值,以此类推,遍历原始输入图像的各个像素点,卷积计算得到特征图output输出。
set_seed() # 设置随机种子
# ================ 2d卷积==============
flag = 1
# flag = 0
if flag:
# 创建1个2d卷积层:输入通道是3通道,1个卷积核、卷积核大小是3*3
conv_layer = nn.Conv2d(3, 1, 3) # input:(i, o, size) weights:(o, i , h, w)
nn.init.xavier_normal_(conv_layer.weight.data) # 对conv_layer进行xavier初始化
# calculation
img_conv = conv_layer(img_tensor)
设置随机种子参数值不同时,该卷积运算得到的特征图也有所不同。
1、以下面lena实验图为例:
当设置随机种子参数值为1即set_seed(1)时,特征图如下右:
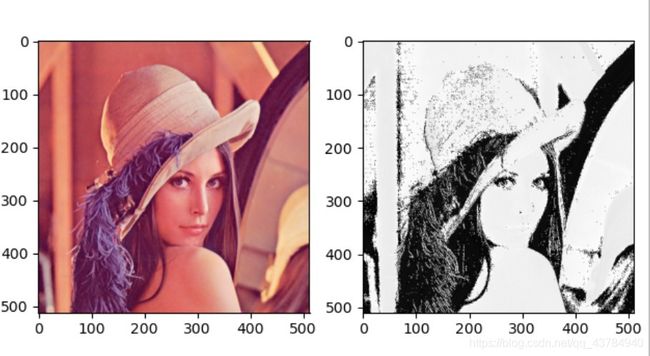
当设置随机种子参数值为2即set_seed(2)时,特征图如下右:
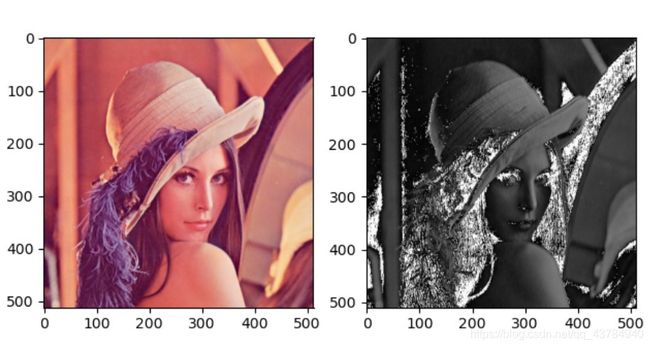
这里选取不同的随机种子参数值,相当于对卷积核的权值进行不同的初始化,得到是不同的卷积核模式,卷积得到的便是不同的特征图。
2、Alexnet卷积核可视化

lena实验图和可视化的卷积核都说明:
(1)卷积核:可以认为是某种模式、某种特征(代表边缘、色彩等细节模式)。
(2)卷积过程:类似于用一个模板到图像上寻找与模板相似的区域,与卷积核模式越相似,激活值越高,从而实现特征提取。
(3)因此,卷积核又可以称为滤波器、过滤器、特征提取中的检测器。
在深度学习中,卷积核具体是哪一种特征、模式,是由模型学习而来的。
如何区分1d卷积、2d卷积、3d卷积?

卷积维度
一般情况下,卷积核在几个维度上滑动,就是几维卷积,如上图所示。
准确地说,是1个卷积核在1个信号上进行几维滑动,就是几维卷积。
Pytorch中卷积实现—nn.Conv2d()
nn.Conv2d()
功能:对多个二维信号进行二维卷积
nn.Conv2d(in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros')
主要参数:
in_channels:(待卷积数据的)输入通道数
out_channels:输出通道数,也等于卷积核个数
kernel_size:卷积核尺寸
stride:步长(通常决定了输出特征图的尺寸大小)
padding:填充个数(可用来保持输入和输出图像尺寸大小匹配)
dilation:空洞卷积大小
groups:分组卷积设置
bias:偏置
一、理论
(1)填充padding:无、有填充padding对卷积运算输出特征图的影响,有填充时输入输出图像尺寸保持不变:
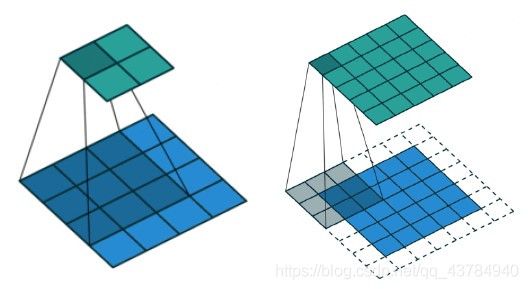
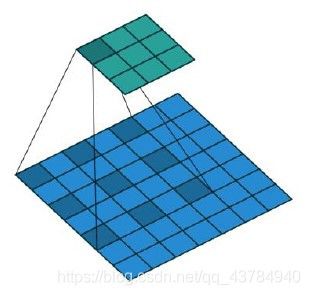
(2)空洞卷积dilation:阴影部分代表权值,权值之间存在间隔。这样的卷积核常用于图像分割任务,主要目的在于提高感受野。
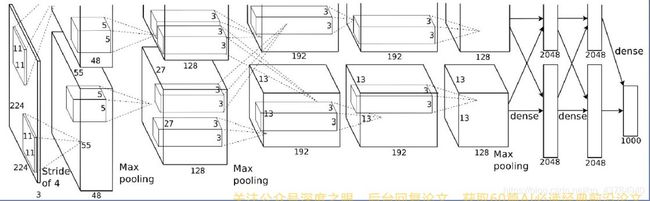
(3)分组卷积设置groups:常用于模型的轻量化。如图所示是Alexnet模型结构,可以看出第1次卷积,模型将输入图像数据分成了上下2组,然后分别进行后续的池化、卷积操作;在特征提取环节,上下2组信号是完全没有任何联系的。直到达到全连接层,才将上、下2组融合起来。这里,第一次的卷积分组设置即可通过groups达到。
(4)卷积操作后,图像尺寸的变化
简化版(不带padding、dilation等操作):
I n s i z e − K e r n e l s i z e s t r i d e + 1 = o u t s i z e . \frac{Insize-Kernelsize}{stride}+1=outsize\,. strideInsize−Kernelsize+1=outsize.
完整版:
I n s i z e + 2 p a d d i n g [ 0 ] − d i l a t i o n [ 0 ] × ( k e r n e l s i z e [ 0 ] − 1 ) − 1 s t r i d e [ 0 ] + 1 = o u t s i z e . \frac{Insize+2padding[0]-dilation[0]\times(kernelsize[0]-1)-1}{stride[0]}+1=outsize\,. stride[0]Insize+2padding[0]−dilation[0]×(kernelsize[0]−1)−1+1=outsize.
二、实验
代码来自深度之眼余老师
set_seed() # 设置随机种子
# ============ load img 加载1张lena图像 =============
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png") # 读取1张RGB图像
img = Image.open(path_img).convert('RGB') # 0~255 采用PIL形式读取
# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()]) # RGB转换成张量
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0) # C*H*W to B*C*H*W unsqueeze拓展到4维张量,增加batch_size维度
# ========create convolution layer 创建卷积层=========
# ================ 2d
flag = 1
# flag = 0
if flag:
# 创建1个2d卷积层,输入通道是3、1个卷积核、卷积核大小是3*3
conv_layer = nn.Conv2d(3, 1, 3) # input:(i, o, size) weights:(o, i , h, w)
nn.init.xavier_normal_(conv_layer.weight.data) # 对conv_layer进行xavier初始化
# calculation
img_conv = conv_layer(img_tensor)
对上述nn.Conv2d进行debug,单步调试可以看到创建好了1个卷积层 Conv_layer。由于该层只有1个卷积核,该层看到参数中显示:卷积核形状是1个4D张量
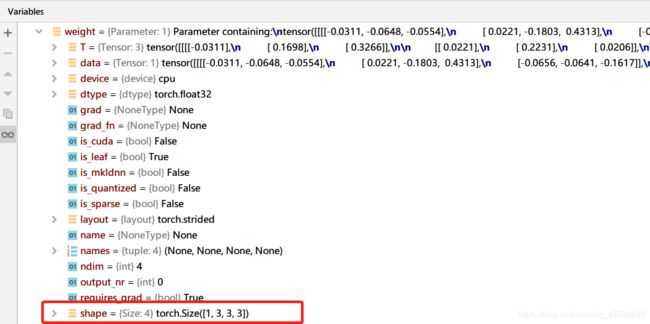
在4D张量[1,3,3,3]中:
(1)[1,3,3,3]:1表示输出通道数,即卷积核个数,由于创建的卷积层中只有1个卷积核,因此该值为1;
(2)[1,3,3,3]:3表示输入图像通道数
(3)[1,3,3,3]:3,3表示该卷积核的尺寸是3×3。
由此可以看出[1,3,3,3]表示1个3×3×3的3D张量,那么该3D张量是如何实现对RGB图像的二维卷积的?
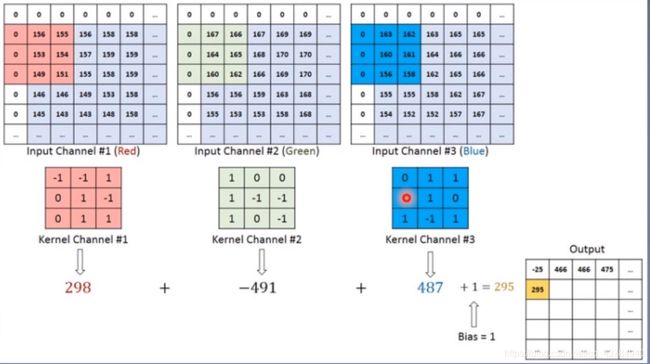
其实质是,1个卷积核始终在1个二维信号上进行卷积。至于为什么卷积核最终形成了1个3D张量,原因在于:输入信号具有3个信号,即输入图像具有R、G、B 3通道。该卷积核需要对3个信号分别进行卷积,由此使得卷积核形成了3D张量,但在3通道上进行的仍旧是2d卷积。
该卷积核分别在R、G、B 3通道进行2d卷积运算,然后将3个通道各自的卷积值相加再加上 偏置项等于输出特征图上某一像素点的值
Pytorch中转置卷积—nn.ConvTranspose
转置卷积又称为部分跨越卷积(Fractionally-strided Convolution),用于对图像进行上采样(UpSample)
nn.ConvTranspose2d()
功能:转置卷积实现上采样
主要参数同nn.Conv2d()
一、理论:
与Conv2d() 区别在于:转置卷积操作后,图像尺寸的变化
简化版(不带padding、dilation等操作):
s t r i d e × ( I n s i z e − 1 ) + K e r n e l s i z e = o u t s i z e . \\stride\times (Insize-1)+Kernelsize=outsize\,. stride×(Insize−1)+Kernelsize=outsize.
完整版:
( I n s i z e − 1 ) × s t r i d e [ 0 ] − 2 × p a d d i n g [ 0 ] + d i l a t i o n [ 0 ] × ( k e r n e l s i z e [ 0 ] − 1 ) + o u t p u t p a d d i n g [ 0 ] + 1 = o u t s i z e . \\(Insize-1)\times stride[0]-2\times padding[0]+dilation[0] \times (kernel_size[0]-1)+outputpadding[0]+1=outsize\,. (Insize−1)×stride[0]−2×padding[0]+dilation[0]×(kernelsize[0]−1)+outputpadding[0]+1=outsize.
二、实验
转置卷积后得到的特征图会出现棋盘效应,这是由于转置卷积的不均匀重叠导致的,解释和解决方法论文《Deconvolution and Checkerboard Artifacts》给出。