2020牛客暑期多校训练营(第二、三、四场)
目录
- 第二场
- A.All-with-Pairs
- G.Greater-and-Greater
- 第三场
- C.Operation-Love
- E.Two-Matchings
- F.Fraction-Construction-Problem
- G.Operating-on-a-Graph
- 第四场
- H.Harder-Gcd-Problem
第二场
第二场感觉适合补的题比较多。
A.All-with-Pairs
可以通过map记录所有后缀出现的次数,并对每个前缀都计算它出现在后缀的次数,复杂度O(n)。但需要考虑到重复计算的情况(比如每当aba前后缀匹配时,会有一个a被重复计算)。
解决方法是预处理出类似于kmp算法中的nxt数组,从前往后扫一遍cnt[nxt[j]]-=cnt[j]。细节要扣清楚还是挺麻烦的。
使用map时不能直接将string作为键值(会爆内存),需要对字符串取不同的参数做两次哈希,把一对哈希值作为键值。
#includeG.Greater-and-Greater
本质上是dp。用dp[i][j]表示 ∀ k ∈ [ 0 , m ] \forall k \in[0,m] ∀k∈[0,m]满足 a i + k > b j + k a_{i+k}>b_{j+k} ai+k>bj+k (考虑 [ a i , a i + 1 , . . . , a i + m − j ] 和 [ b j , b j + 1 , . . . , b m ] [a_i,a_{i+1},...,a_{i+m-j}]和[b_j,b_{j+1},...,b_{m}] [ai,ai+1,...,ai+m−j]和[bj,bj+1,...,bm])
画张图表示一下,dp[i][j]=1就表示第一段的每一位都大于等于第二段:
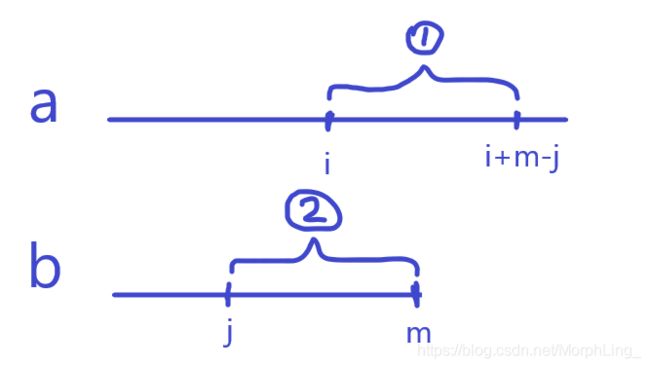
接下来考虑转移,在已知dp[i][j]=1的情况下,要确定dp[i-1][j-1](即图中的三、四两段),只需要再比较a[i-1]和b[i-1]的大小即可

写成代码就是
if (dp[i][j] && a[i-1]>=b[j-1]) dp[i-1][j-1]=1;
最后只要统计dp[i][1]的数量就是答案了。
但如果用常规方法来实现这个dp,无论空间还是时间上都是不可做的,然而bitset可以。(bit比bool节约八倍空间,位运算节约时间)思想其实就是上面dp的思路,只不过要实现出来真的只能说是神仙操作。
#include
using namespace std;
const int N=1.5e5+5,M=4e4+5;
bitset<M>cur,S[M],ns,I;
int T,n,m,ans;
int A[N],B[M],ord[M];
int fd(int x)
{
int l=0,r=m;
while(l<r)
{
int mid=(l+r)>>1;
if (B[ord[mid+1]]<=x)
l=mid+1;
else r=mid;
}
return l;
}
int main()
{
cin>>n>>m;
for (int i=1;i<=n;i++) scanf("%d",&A[i]);
for (int i=1;i<=m;i++)
{
scanf("%d",&B[i]);
ord[i]=i;
}
sort(ord+1,ord+1+m,[&](int u,int v){
return B[u]<B[v];
});
for (int i=1;i<=m;i++)
{
S[i]=S[i-1];
S[i].set(ord[i]);
}
I.set(m);
for (int i=n;i>=1;i--)
{
ns=S[fd(A[i])];
cur=((cur>>1)|I)&ns;
if (cur[1]) ans++;
}
printf("%d\n",ans);
return 0;
}
第三场
C.Operation-Love
按照顺序依次计算两点之间的距离
如果(a,b)长度为6,(b,c)长度为1,说明(a,b)是拇指的线段(指向指尖)
如果(a,b)长度为6,(b,c)长度为9,说明(b,a)是拇指的线段(指向指尖)
如果是左手,那么其他所有点都在拇指线段的左侧,反之则在右侧。
判断点在线段左侧还是右侧可以通过叉乘的方法。
假设线段为(x1,y1)->(x2,y2),点坐标为(x0,y0)
那么计算(x2-x1,y2-y1)×(x0-x1,y0-y1)的值,<0为右侧,>0为左侧
#include
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int MAXN=2e3+5;
const double eps=1e-4;
class Point {
public:
double x,y;
bool operator !=(Point &P)
{
return fabs(x-P.x)>eps && fabs(y-P.y)>eps;
}
Point(double a=0,double b=0):x(a),y(b){}
};
class Line {
public:
bool ifk;
double dis;
double k,b;
//求过两点的直线
void mkline (Point A,Point B) {
dis=sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));
ifk=true;k=b=0;
if (A.x==B.x) {
ifk=0;
b=A.x;
} else {
if (A.y==B.y) {
k=0;
b=(A.x+B.x)/2;
} else {
k=(B.y-A.y)/(B.x-A.x);
b=A.y-k*A.x;
}
}
}
//求两点中垂线
void mkbisector (Point A,Point B) {
ifk=true;k=b=0;
if (A.x==B.x) {
k=0;
b=(A.y+B.y)/2;
} else if (A.y==B.y) {
ifk=0;
b=(A.x+B.x)/2;
} else {
k=-1/(B.y-A.y)*(B.x-A.x);
b=(A.y+B.y)/2-k*(A.x+B.x)/2;
}
}
bool operator == (Line &T) {
return (ifk==T.ifk) && fabs(k-T.k)<eps && fabs(b-T.b)<eps;
}
};
Point p[30];
Line l[30];
int T;
int main()
{
cin>>T;
while(T--)
{
for (int i=1;i<=20;i++)
{
cin>>p[i].x>>p[i].y;
}
p[21]=p[1];
for (int i=1;i<=20;i++)
{
l[i].mkline(p[i],p[i+1]);
}
l[21]=l[1];
Point a,b,c;
for (int i=1;i<=20;i++)
{
if (fabs(l[i].dis-6)<eps && fabs(l[i+1].dis-1)<eps)
{
a=p[i],b=p[i+1];
}
if (fabs(l[i].dis-6)<eps && fabs(l[i+1].dis-9)<eps)
{
a=p[i+1],b=p[i];
}
}
for (int i=1;i<=20;i++)
if (p[i]!=a && p[i]!=b)
{
c=p[i];
break;
}
double p=b.x-a.x,q=b.y-a.y,w=c.x-a.x,o=c.y-a.y;
if (p*o-q*w<0) printf("right\n");
else printf("left\n");
}
return 0;
}
E.Two-Matchings
本身是一个图论问题,要使得每个点都连上两条边且边的权值和最小,权值为两个数之差的绝对值。可以把n个数从小到大排序,把问题变成在一列有序数上连线的问题。
首先考虑到n=4或n=6的情况,可以发现此时答案是固定的,也就是(A[n]-A[1])*2,而对于n>=8的情况,总是可以拆成若干个长度为4或6的分块,并使答案减少分块连接处的两数之差。也就是dp[n]总是从dp[n-4]或dp[n-6]减去连接处的权值后转移过来,这样就可以通过dp计算答案了。
#includeF.Fraction-Construction-Problem
如果a,b不互质那么答案比较显然,取 a b \frac{a}{b} ba约分之后的分母即可。
考虑a、b互质的情况,把原式转换成 c f − e d d f = a b \frac{cf-ed}{df}=\frac{a}{b} dfcf−ed=ba
如果b自身是质数或者1,那么d、f中至少有一个大于等于b,不符合条件。
如果b不是质数且不是1,那么d总能分解成两个互质因子,令b的两个互质因子分别为d、f,那么由扩展欧几里得算法可知 c f − e d = a cf-ed=a cf−ed=a一定有整数解。将d、f代入后求正整数解即可。
为了求d的互质因子,在素数筛中可以加入pfactor[i]数组记录i的第一个质因数。将第一个质因数全部取出后,分离出的两个数一定互质。
#includeG.Operating-on-a-Graph
其实就是并查集,但是需要一些技巧。
两个重点,一是启发式合并,将b合并入a时,若b中元素较多,则直接交换a、b中的元素。
二是合并前清空原有的元素,合并后只保留新增的元素。
#include第四场
H.Harder-Gcd-Problem
构造。除了1和大于n/2的质数,若剩下的数的个数为偶数则都能匹配,若为奇数则只有一个不能匹配。
从大到小考虑所有小于等于n/2的素数p,将未被访问的p的倍数加入集合,若集合大小为偶数,则恰好两两匹配,若集合大小为奇数,则取出p*2这个数(因为2是最后考虑的素数,所以p*2一定没有被访问过),剩下的两两匹配。最后把所有取出来的数再两两匹配一下(都是2的倍数)
#include