【前端js】实现剑指offer|leetcode(二)——数组题目集合
文章目录
- 一、数组去重
- 1. 对排序数组去重(leetcode 26. 删除排序数组中的重复项)
- 2. 检查是否存在重复元素(leetcode 217. 存在重复元素)
- 3. 检查相邻k个元素是否存在重复元素(leetcode 219. 存在重复元素 II)
- 二、查找数组中的元素
- 1. leetcode 26. 两数之和
- 2.数组中出现次数超过一半的数字(牛客网-剑指 offer)
- 3. 旋转数组的最小数字(牛客网-剑指 offer)
- 三、数组排序
- 1.打乱数组顺序
- 2.最小的K个数
- 3.合并两个有序数组
- 4.颜色分类——重复数组排序(leetcode 75. Sort Colors)
- 四、数组子序列
- 1. 连续子数组的最大和(剑指offer-时间效率)
- 2. 买卖股票的最佳时机(leetcode 121)
- 2. 买卖股票的最佳时机2(leetcode 122)
- 五、多维数组
- 1. 构建乘积数组(剑指 offer:数组合集)
- 2. 二维数组中的查找(剑指 offer:数组合集)
- 六、生成新数组
- 1. 汉诺塔盖大楼(2019腾讯春招前端笔试题)
一、数组去重
1. 对排序数组去重(leetcode 26. 删除排序数组中的重复项)
题目:https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/
给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
思路
- 给定的数组 nums是一个排过序的数组,那么,重复元素一定是在数组中相邻的元素。也就是说,我们可以通过遍历数组,找出相邻相同项,并将其从数组中移除即可
- 需要原地删除,那么我们就不能创建一个副本,而是只能在原数组上进行操作
参考:https://blog.csdn.net/qq_30216191/article/details/81348501 - 特殊情况 数组长度小于等于1,return
- 遍历数组,比较当前和下一位
- 如果相等删除一位,并把
i--,否则会跳过下个元素 - 遍历完成,返回数组长度
var removeDuplicates = function(nums) {
if (nums.length <= 1) {
return nums.length;
}
for (let i = 0; i < nums.length; i++) {
if (nums[i] === nums[i + 1]) {
nums.splice(i, 1);
i--;
}
}
return nums.length;
};
removeDuplicates([1, 1, 2]);
2. 检查是否存在重复元素(leetcode 217. 存在重复元素)
题目:https://leetcode-cn.com/problems/contains-duplicate/
方法一:对象键值法
var containsDuplicate = function(nums) {
if(nums.length<=1){
return false;
}
let obj = {};//对照对象
for (var i = 0; i < nums.length; i++) {
// 判断当前项是否遍历过,是则删除,否存入obj以作对照
if (obj[nums[i]]) {
return true
//数组删除了一项,要把i回退一下,不然会跳过下一项不去遍历
} else {
obj[nums[i]] = 1;
}
}
return false;
};
方法二:set法,比较去重数组和原数组的长度
var containsDuplicate = function(nums) {
if(nums.length<=1){
return false;
}
let uniq=[...new Set(nums)];
return !(uniq.length===nums.length);
};
3. 检查相邻k个元素是否存在重复元素(leetcode 219. 存在重复元素 II)
题目:https://leetcode-cn.com/problems/contains-duplicate-ii/
给定一个整数数组和一个整数 k,判断数组中是否存在两个不同的索引 i 和 j,使得 nums [i] = nums [j],并且 i 和 j 的差的绝对值最大为 k。
对每一个元素,使用includes方法判断[index+1~index+k+1]的范围内是否有重复元素
some() 方法会依次执行数组的每个元素: 如果有一个元素满足条件,则表达式返回true , 剩余的元素不会再执行检测。
如果没有满足条件的元素,则返回false。
array.some(function(currentValue,index,arr),thisValue)
includes() 方法用来判断一个数组是否包含一个指定的值,如果是返回 true,否则false。
arr.includes(searchElement, fromIndex)
//是否存在重复元素2
/**
* @param {number[]} nums
* @param {number} k
* @return {boolean}
*/
var containsNearbyDuplicate = function(nums, k) {
//some遍历得到第一个函数的返回值为true,就会return true,如果q
return nums.some((item, index) => {
return nums.slice(index + 1, index + k + 1).includes(item);
});
};
二、查找数组中的元素
1. leetcode 26. 两数之和
题目:https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
方法一:indexof用法 (慢)
b = nums.indexOf(target - nums[i]);
实际上是对数组再遍历一次,虽然在写法上有优化,但是实际时间复杂度还是O(N*N)。
如何快速地在数组中检索值?使用 indexOf 其实已经在数据中检索特定值的思路上了。只不过 indexOf 内部还是对数组进行循环检索,因此并没有达到更快的要求。在这方面, hash表 可以帮助到我们。
比如我们有一个对象 obj = { …, a: 1} ,当我们取值 Obj.a 时,是个直接寻址的过程,因此效率是很高的。
方法二:使用对象索引(快)
我们创建一个对象,并给它赋值,对象的键值是我们想要检索的值,对象的值是在数组中的索引。nums.forEach((e, i) => mapObj[e] = i);然后遍历查找对象:mapObj[targer - nums[i]];
方法三:使用map(最快最好)
Map是一组键值对的结构,具有极快的查找速度。map的格式:
var twoSum = function(nums, target) {
let map = {};
if ((nums.length <= 1)) {
return [];
}
let res = [];
// nums.forEach((e, i) => map.set(e, i));//map.set存放键值对
for (let i = 0; i < nums.length; i++) {
let num = nums[i];
/* 不存在时,存入 */
if (!map[num]) {
map[num] = i;
}
/* 判断是否有差值存在 */
let j = map[target - num];
if (j !== undefined && j !== i) {
res.push([i, j]);
}
}
return res;
};
2.数组中出现次数超过一半的数字(牛客网-剑指 offer)
牛客网-数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
思路
- 特殊情况:长度为1/0
- 新建map,遍历数组,依次储存数组值和频率
- 如果map里有item这一项,频率value+1,并判断是否超过
Math.floor(numbers.length / 2),超过则return, - 注意需要循环内return,所以必须使用
for循环,不能使用foreach - 如果map里没有item这一项,频率value为1
- 循环结束没有返回,说明数组不存在这样的元素
function MoreThanHalfNum_Solution(numbers) {
// write code here
if (numbers.length === 0) return 0;
if (numbers.length === 1) return numbers[0];
let map = new Map();
for (let i = 0; i < numbers.length; i++) {
//map里有item这一项
if (map.has(numbers[i])) {
map.set(numbers[i], map.get(numbers[i]) + 1); //频率value+1
if (map.get(numbers[i]) > Math.floor(numbers.length / 2))
return numbers[i]; //频率value>一半长度,返回
}
//map里没有item这一项
else {
map.set(numbers[i], 1);
} //频率value为1
}
//循环结束没有返回,说明数组不存在这样的元素
return 0;
}
MoreThanHalfNum_Solution([1, 2, 3, 2, 2, 2, 5, 4, 2]);
3. 旋转数组的最小数字(牛客网-剑指 offer)
题目描述
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转,输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。 NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
,min在left~mid中间; - 如果
mid大于right,说明mid-right不是单调递增(mid不会是最小值,但是这中间会有最小值),min在mid+1~right中间; mid=right,说明存在重复元素,不能直接判断单调性,右指针左移一位,依次比较。
- 如果
function minNumberInRotateArray(rotateArray) {
// write code here
// 空数组/单元素数组
if (!rotateArray || rotateArray.length === 1) {
return rotateArray[0] || 0;
}
let left = 0, //左指针
right = rotateArray.length - 1; //右指针
while (left < right) {
let mid = Math.floor((left + right) / 2);
//mid和right相等,最小值一定在right元素的右边
if (rotateArray[mid] === rotateArray[right]) {
right--; //右指针左移动一位,依次比较
}
//mid-right非递增,最小值一定在mid元素的右边
else if (rotateArray[mid] > rotateArray[right]) {
left = mid + 1; //左指针移动到mid右边第一位
}
//mid-mid递增,最小值一定在mid/mid元素的
else right = mid; //右指针移动到mid
}
// left和right相遇退出循环,该位置就是最小值
return rotateArray[right];
}
三、数组排序
1.打乱数组顺序
leetcode 384. Shuffle an Array
打乱数组顺序,没有重复元素
Fisher–Yates shuffle洗牌算法
- Step1:从数组末尾开始遍历,选取当前i位置的元素。然后从
0-i随机产生一个位置k,交换a[k]和a[i] - Step2:每次遍历,都只从当前位置前面生成随机位置,因为后面的元素已经乱序
Math.floor(Math.random() * (arr.length - i ))生成0-i的随机位置


参考; https://blog.csdn.net/duola8789/article/details/78749917
var Solution = function(nums) {
this.nums = nums;
};
/**
* Resets the array to its original configuration and return it.
* @return {number[]}
*/
Solution.prototype.reset = function() {
return this.nums;
};
/**
* Returns a random shuffling of the array.
* @return {number[]}
*/
Solution.prototype.shuffle = function() {
//交换数组元素顺序
const swap = (a, i, j) => {
[a[i], a[j]] = [a[j], a[i]];
};
let arr = this.nums.slice(); //深拷贝数组,不然会影响reset的输出
for (let i = arr.length - 1; i >= 0; i--) {
swap(arr, i, Math.floor(Math.random() * (arr.length - i )));
//swap(arr, i, Math.floor(Math.random() *i ));
}
return arr;
};
2.最小的K个数
牛客网剑指offer——数组合集
输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,。
方法一:sort法
sort正序排序,返回前k个元素:
function GetLeastNumbers_Solution(input, k)
{
if (input.length < k) return [];
return input.sort((a,b)=>(a-b)).slice(0,k);
}
方法二:大顶堆法
- 取前k个元素构建大顶堆
- 从前向后遍历
k-len元素, - 元素大于大顶堆的根,说明他不可能在最小的k个数里面,跳过这次循环
- 元素小于大顶堆的根,说明大顶堆的根在最小的k个数里面,当前元素可能在最小的k个数里面,交换大顶堆的根和当前元素,并重新维护这个堆
*基于堆排序算法,构建最大堆。时间复杂度为
O(nlogk)
*如果用快速排序,时间复杂度为O(nlogn);
*如果用冒泡排序,时间复杂度为O(n*k)
function GetLeastNumbers_Solution(input, k)
{
// write code here
if (input.length < k) return [];
// let kLeasts = input.slice(0, k - 1);
buildHeap(input, k); //取前k个元素构建大顶堆
for (let i = k; i < input.length; i++) {
if (input[i] > input[0]) continue; //元素大于大顶堆的根,跳过
swap(input, i, 0); //元素小于大顶堆的根,交换大顶堆的根和当前元素
headAdjust(input, 0, k); //调整大顶堆
}
return input.slice(0, k).sort((a, b) => a - b);//题目要求生序排序
}
function swap(a, i, j) {
[a[i], a[j]] = [a[j], a[i]];
}
//从输入节点处调整堆
function headAdjust(arr, cur, len) {
let childMax = 2 * cur + 1; //指向子树中较大的位置,初始值为左子树的索引
//子树存在(索引没超过数组长度)而且子树值大于根时,此时不符合大顶堆结构,进入循环,调整堆的结构
while (childMax < len) {
//判断左右子树大小,如果右子树更大,而且右子树存在,childMax指针指向右子树
if (arr[childMax] < arr[childMax + 1] && childMax + 1 < len) childMax++;
//子树值小于根节点,不需要调整,退出循环
if (arr[childMax] < arr[cur]) break;
//子树值大于根节点,需要调整,先交换根节点和子节点
swap(arr, childMax, cur);
cur = childMax; //根节点指针指向子节点,检查子节点是否满足大顶堆规则
childMax = 2 * cur + 1; //子节点指针指向新的子节点
}
}
// 对arr的前k个元素,建立大顶堆
function buildHeap(arr, k) {
//从最后一个非叶子节点开始,向前遍历,
for (let i = Math.floor(k / 2 - 1); i >= 0; i--) {
headAdjust(arr, i, k); //对每一个节点都调整堆,使其满足大顶堆规则
}
}
3.合并两个有序数组
leetcode 88. Merge Sorted Array
给定两个有序整数数组 nums1 和 nums2,将 nums2 合并到 nums1 中,使得 num1 成为一个有序数组。
思路
- 合并数组的长度为
n + m,从后往前遍历数组,往数组里存入两个数组中的较大的值 - 数组1的数被存完以后,开始从将数组2的数组依次存入
var merge = function(nums1, m, nums2, n) {
//if (m === 0 || n === 0) return [].concat(nums1, nums2);
let [i, j, index] = [m - 1, n - 1, n + m - 1];
while (i >= 0 && j >= 0) {
nums1[i] >= nums2[j]
? (nums1[index--] = nums1[i--])
: (nums1[index--] = nums2[j--]);
}
while (j >= 0) {
nums1[index--] = nums2[j--];
}
};
4.颜色分类——重复数组排序(leetcode 75. Sort Colors)
leetcode 75. Sort Colors
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。你能想出一个仅使用常数空间的一趟扫描算法吗?
方法一:计数法——两次遍历
思路
- 首先遍历一遍原数组,分别记录 0,1,2 的个数。
- 然后更新原数组,按个数分别赋上 0,1,2。
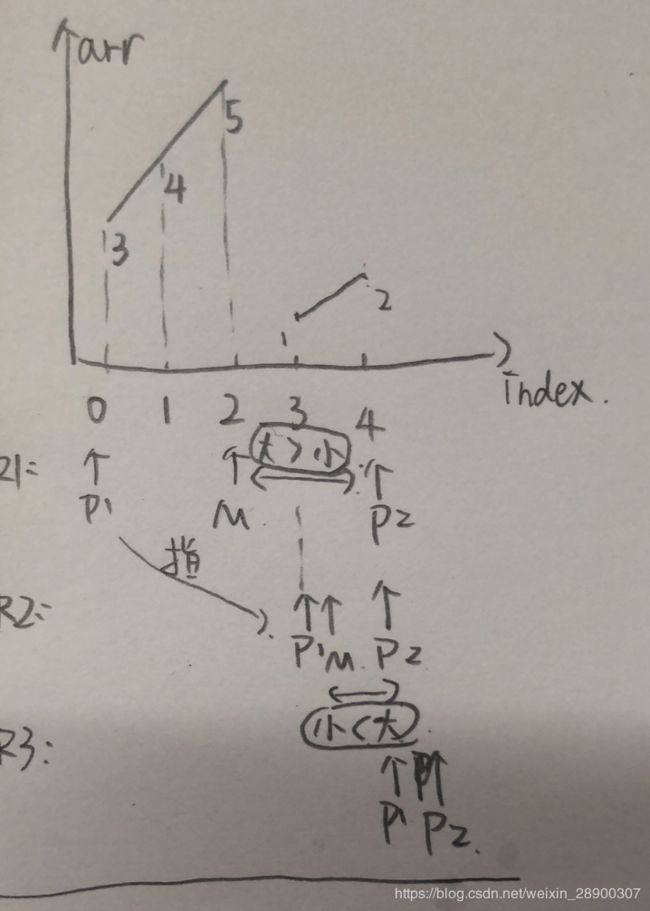
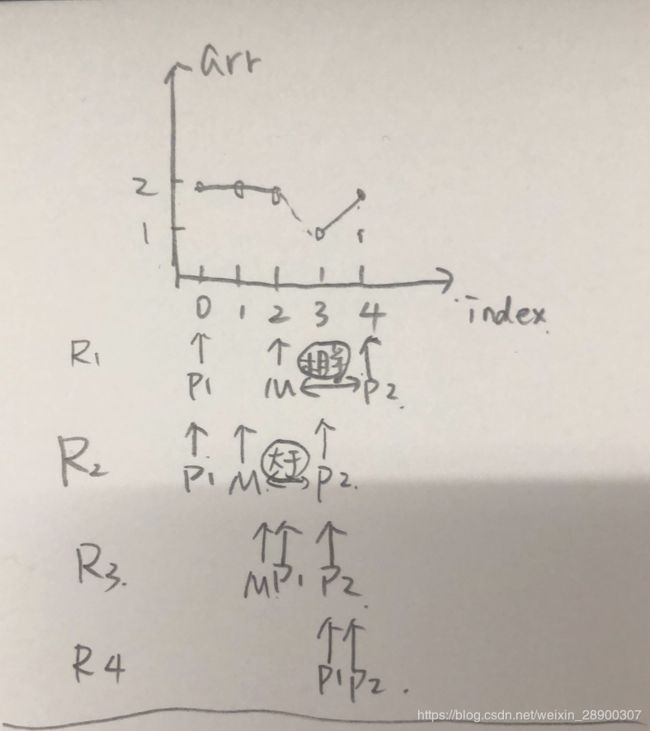
方法二:双指针分区法——一次遍历
思路
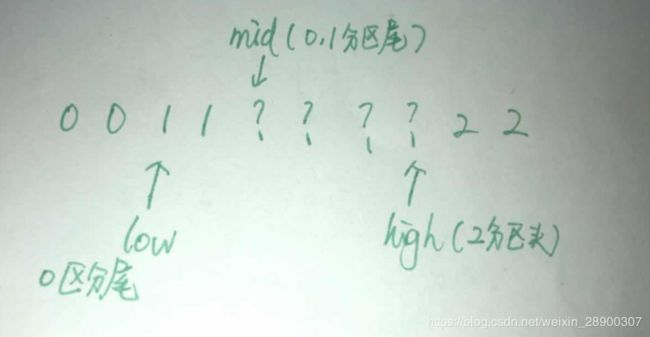
- 定义三个指针:
low指向0分区的下一个位置,mid指向1分区的下一个位置,high指向2分区的前一个位置。 - 如图所示,0区块在前,1区块在中间,2区块在后,中间的
?代表尚未遍历的数字,值不确定。 mid指针遍历数组- 如果
mid为0,交换low和mid的元素,low和mid都下移一位,0分区增加一个元素 - 如果
mid为1,mid下移一位,1分区增加一个元素 - 如果
mid为2,交换high和mid的元素,high向前移动一位,2分区增加一个元素,mid不移动,因为mid元素还需要再进行下一轮比较,不一定是1分区的元素
代码
var sortColors = function(nums) {
if (nums.length <= 1) return nums;
let low = 0,
i = 0,
high = nums.length - 1;
while (i <= high) {
switch (nums[i]) {
case 0:
swap(nums, i++, low++);
break;
case 2:
swap(nums, i, high--);
break;
case 1:
i++;
break;
}
}
return nums;
};
var swap = function(a, i, j) {
[a[i], a[j]] = [a[j], a[i]];
};
四、数组子序列
1. 连续子数组的最大和(剑指offer-时间效率)
题目描述,点击查看原题
输入一个整型数组,数组里有正数也有负数。数组中一个或连续的多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为O(n)。
方法一:枚举法
思路:
- 枚举出数组的所有子数组并求出它们的和。一个长度为n的数组,总共有
n(n+1)/2个子数组。 - 对数组内每一个数A[i]进行遍历,然后遍历
以它们为起点的子数组,比较各个子数组的大小,找到最大连续子数组; - 计算出所有子数组的和,两层遍历,最快也需要
O(n2)的时间
方法二:遍历法
思路:
- 找最大子序列之和,等价于一段找
连续的子序列,和是最大值,因为和为负的子序列会减少和,所以直接抛弃这个子序列和更大 特殊情况:数组为空/单元素- 数组
全是负数时,最大和为数组中的最大值 - 数组
有正数时,从头到尾逐个累加数组中的每个数字,存放到curSum,如果curSum小于0,抛弃之前的累加值,重新开始计数,curSum=item; - 比较
curSum和maxSum,取最大值,存进maxSum,为当前历史序列和的最大值

function FindGreatestSumOfSubArray(array)
{
// write code here
//数组为空/单元素
if (array.length === 0) return 0;
if (array.length === 1) return array[0];
//全是负数时,最大和为数组中的最大值
if(array.every(item => item < 0)) {
return Math.max(...array);
}
//数组有正数时,要遍历比较最大和
let curSum,
maxSum = 0;
array.forEach((item, index) => {
curSum = curSum > 0 ? curSum + item : item;
maxSum = Math.max(curSum, maxSum);
});
return maxSum;
}
2. 买卖股票的最佳时机(leetcode 121)
题目描述,点击查看原题
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。
方法一:O(n)遍历法
思路:
- 等价于找一个数组的
两个元素子序列,使得他们差值最大,要求小元素在前,大元素在后 - 遍历数组,
i指向卖出天数 maxProfit保存最大利润,是0~i-1之间的差值的最大值,每次最大值只能在当前元素-当前元素之前的最小买入价以及上次保存的最大利润中产生。因为要使用当前元素之前的minPrice,所以先比较更新maxProfitminPrice保存最小买入价,是0~i-1之间的最小值,每次比较当前值和上次保存的最小值- 遍历完成以后的
maxProfit就是整个数组中的最大差值

代码
var maxProfit = function(prices) {
if (prices.length <= 1) return 0;
let minPrice = prices[0], //最小买入价,初始化为第一个价格
maxProfit = 0; //最大利润,初始为0
for (let i = 0; i < prices.length; i++) {
maxProfit = Math.max(maxProfit, prices[i] - minPrice); //和当前价和最小买入价之差比较,更新最大利润
minPrice = Math.min(minPrice, prices[i]); //和当前价格比较,更新最小买入价
}
return maxProfit;
};
2. 买卖股票的最佳时机2(leetcode 122)
题目描述,点击查看原题
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
思路
- 比较数组
相邻元素,后一位比较大,就把差值累加到结果上
代码
var maxProfit = function(prices) {
if (prices.length <= 1) return 0;
let res=0;
for (let i = 1; i < prices.length; i++) {
prices[i] > prices[i - 1] ? (res += prices[i] - prices[i - 1]) : "";
}
return res;
};
五、多维数组
1. 构建乘积数组(剑指 offer:数组合集)
题目描述,点击查看原题
给定一个数组A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中B中的元素B[i]=A[0]A[1]…*A[i-1]A[i+1]…*A[n-1]。不能使用除法。
思路:
B[i]的值可以看作下图的矩阵中每行的乘积。也就是剔除矩阵i行数组中索引为i的元素以后,其他元素的乘积。
- 特殊情况: 长度小于等于1,返回自身
- 新建数组存放结果
for循环遍历矩阵每一行.filter方法剔除矩阵i行数组中,索引为i的元素.reduce方法将新数组的所有元素连乘- 返回值压入result数组
- 循环完成,返回数组
function multiply(array) {
// write code here
//长度小于等于1,返回自身
if (array.lenght <= 1) {
return array;
}
//新建数组存放结果
var result = [];
//遍历0~array.length-1,矩阵的第一行到最后一行
for (let i = 0; i < array.length; i++) {
//.filter方法剔除矩阵i行数组中,索引为i的元素
//.reduce方法将新数组的所有元素连乘
//返回值压入result数组
result.push(
array
.filter((item, index) => index != i)
.reduce((cur, pre) => cur * pre, 1)
);
}
return result;
}
multiply([1, 2, 3]);
2. 二维数组中的查找(剑指 offer:数组合集)
题目描述,点击查看原题
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
思路
- 定位右上角元素:比它小的元素都在它同行左侧,比它大的元素都在它的下面的行
- while循环:当元素坐标在边界内,进入循环
- 判断目标值和坐标元素大小关系
- 相等,查找成功,return
- 大于,应该在它的下面的行,y坐标行数加一,进入下一轮循环
- 小于,应该在它的同行左侧,x坐标列数减一,进入下一轮循环
- 循环结束,return
function Find(target, array) {
//右上角元素
var i = array.length - 1;
var j = 0;
//当元素坐标在边界内,进入循环
while (i >= 0 && j < array[i].length) {
if (target == array[i][j]) {
//目标值就是坐标元素,return
return true;
} else if (target > array[i][j]) {
//目标值大于坐标元素,y坐标行数加一
j++;
continue;
} else if (target < array[i][j]) {
//目标值大于坐标元素,x坐标列数减一
i--;
continue;
}
}
return false;
}
六、生成新数组
1. 汉诺塔盖大楼(2019腾讯春招前端笔试题)
n天盖完一栋大楼,每天运来一个模块,面积 ,要求必须最大的模块先搭,然后搭建面积-1的模块,依次往上,直到搭建完所有模块
,要求必须最大的模块先搭,然后搭建面积-1的模块,依次往上,直到搭建完所有模块
输入数据组数,每组数据包含两个:1.总天数,2,每天运来的模块的面积组成的数组
要求输出:n行数据,每一行为当天搭建的模块,按顺序排列的一个数组;如果当天没有搭建模块,则当前数组元素为empty

/**
*主程序
*
* @param {*} cnt 组数
* @param {*} cin 输入
*/
function tower(cnt, cin) {
let modalGrp = [];
for (let i = 0; i < cnt; i + 2) {
//将输入数据俩俩一组,放入modalGrp数组
modalGrp[i] = {}; //每组是一个对象
modalGrp[i].day = cin[i]; //day存放天数
modalGrp[i].modal = cin[i + 1]; //modal存放每天运来的模块数组
getDaliyModal(modalGrp[i]);
}
/**
*输出一组工程的模块搭建状况,
*
* @param {*} modalGrp 输入的一组工程数据,一个对象,包含day和modal两个属性
* @returns 返回一个数组,索引代表天数,值代表当天搭建的模块
*/
function getDaliyModal(modalGrp) {
if (modalGrp.day <= 1) return modalGrp.modal; //特殊情况,返回自身
let res = []; //存放输出
let max = modalGrp.day; //存放要搜索的模块里的最大值,初始值为modalGrp.day,依次减一
let map = new Map(); //存放modal面积和索引键值对
modalGrp.modal.forEach((item, index) => {
map.set(item, index);
});
let insertIndex = map.get(max); //初始max的索引,
while (max > 0) {
//max小于1,结束循环
//当前max的索引小于max+1的索引时(max比max+1早拿到)/max是初始值时
if (map.get(max) < map.get(max + 1) || max === modalGrp.day) {
res[insertIndex] = res[insertIndex]
? res[insertIndex].concat(max)
: [max]; //在res的初始max的索引位置插入max值
} else {
//当前max的索引大于max+1的索引时(max比max+1晚拿到)
res[map.get(max)] = [max]; //在res的当前max的索引位置插入max值
insertIndex = map.get(max); //把插入位置更新为当前最大值的索引
}
max--;
}
return res;
}
tower(1, [4, [3, 1, 4, 2]]);
// tower(3, [4, [3, 1, 4, 2], 5, [3, 1, 5, 2, 4], 6, [3, 1, 5, 2, 4, 6]]);