pytorch学习笔记(十六)————卷积神经网络
pytorch学习笔记(十六)————卷积神经网络
- 目录
- 发展背景和基本概念
- CNN的引入
- 感受野
- 参数共享
- CNN架构
- 卷积层----CONV
- 什么是卷积?
- 经典卷积核举例
- 卷积层的操作
- 池化层----POOL
目录
发展背景和基本概念
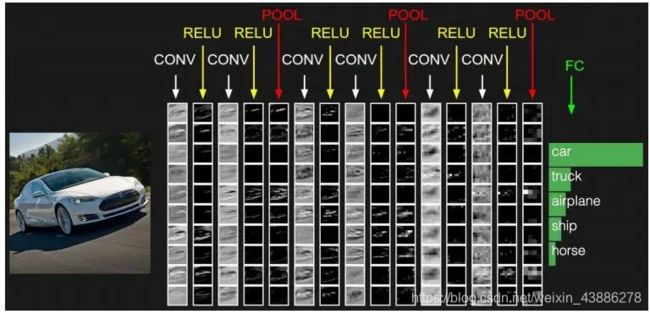
卷积神经网络是目前深度学习技术领域中非常具有代表性的神经网络之一,在图像分析和处理领域取得了众多突破性的进展,在学术界常用的标准图像标注集ImageNet上,基于卷积神经网络取得了很多成就,包括图像特征提取分类、场景识别等。卷积神经网络相较于传统的图像处理算法的优点之一在于避免了对图像复杂的前期预处理过程,尤其是人工参与图像预处理过程,卷积神经网络可以直接输入原始图像进行一系列工作,至今己经广泛应用于各类图像相关的应用中。
从卷积神经网络的提出到目前的广泛应用,大致经历了理论萌芽阶段、实验发展阶段以及大规模应用和深入研究阶段。
(1)理论萌芽阶段。1962年Hubel以及Wiesel通过生物学研究表明,从视网膜传递脑中的视觉信息是通过多层次的感受野(Receptive Field)激发完成的,并首先提出了感受野的概念。1980年日本学者Fukushima在基于感受野的概念基础之上,提出了神经认知机(Neocognitron)。神经认知机是一个自组织的多层神经网络模型,每一层的响应都由上一层的局部感受野激发得到,对于模式的识别不受位置、较小形状变化以及尺度大小的影响。神经认知机可以理解为卷积神经网络的第一版,核心点在于将视觉系统模型化,并且不受视觉中的位置和大小等影响。
(2)实验发展阶段。1998年计算机科学家Yann LeCun等提出的LeNet5采用了基于梯度的反向传播算法对网络进行有监督的训练,Yann LeCun在机器学习、计算机视觉等都有杰出贡献,被誉为卷积神经网络之父。LeNet5网络通过交替连接的卷积层和下采样层,将原始图像逐渐转换为一系列的特征图,并且将这些特征传递给全连接的神经网络,以根据图像的特征对图像进行分类。感受野是卷积神经网络的核心,卷积神经网络的卷积核则是感受野概念的结构表现。学术界对于卷积神经网络的关注,也正是开始于LeNet5网络的提出,并成功应用于手写体识别。同时,卷积神经网络在语音识别、物体检测、人脸识别等应用领域的研究也逐渐开展起来。
(3)大规模应用和深入研究阶段。在LeNet5网络之后,卷积神经网络一直处于实验发展阶段。直到2012年AlexNet网络的提出才奠定了卷积神经网络在深度学习应用中的地位,Krizhevsky(他是hintion的学生对应的论文就是刚开始提到的深度卷积神经网络)等提出的卷积神经网络AlexNet在ImageNet的训练集上取得了图像分类的冠军,使得卷积神经网络成为计算机视觉中的重点研究对象,并且不断深入。在AlexNet之后,不断有新的卷积神经网络提出,包括牛津大学的VGG网络、微软的ResNet网络、谷歌的GoogLeNet网络等,这些网络的提出使得卷积神经网络逐步开始走向商业化应用,几乎只要是存在图像的地方,就会有卷积神经网络的身影。
从目前的发展趋势而言,卷积神经网络将依然会持续发展,并且会产生适合各类应用场景的卷积神经网络,例如,面向视频理解的3D卷积神经网络等。值得说明的是,卷积神经网络不仅仅应用于图像相关的网络,还包括与图像相似的网络,例如,在围棋中分析棋盘等。
基本概念
卷积神经网络中有三个基本的概念:局部感受野(Local Receptive Fields)、共享权值(Shared Weights)、池化(Pooling)。
(1)局部感受野。对于一般的深度神经网络,往往会把图像的每一个像素点连接到全连接的每一个神经元中,而卷积神经网络则是把每一个隐藏节点只连接到图像的某个局部区域,从而减少参数训练的数量。例如,一张1024×720的图像,使用9×9的感受野,则只需要81个权值参数。对于一般的视觉也是如此,当观看一张图像时,更多的时候关注的是局部。
(2)共享权值。在卷积神经网络的卷积层中,神经元对应的权值是相同的,由于权值相同,因此可以减少训练的参数量。共享的权值和偏置也被称作卷积核或滤汲器。
(3)池化。由于待处理的图像往往都比较大,而在实际过程中,没有必要对原图进行分析,能够有效获得图像的特征才是最主要的,因此可以采用类似于图像压缩的思想,对图像进行卷积之后,通过一个下采样过程,来调整图像的大小。
CNN的引入
在早期时代,由于计算机行业的不发达,一张内存能存储的内容有限,往往只有几十-几百kb,而传统的神经网络架构,我们拿MNIST数据集举例
如下图所示

一个普通的神经网络按照以上架构,经过计算就需要390k
个参数,每个参数占4B,共计1.6MB,而当时的80386内存也就几百k
感受野

当时计算机学家借鉴了生物学领域的概念,如上图的小孩,刚开始小孩的视野里关注的只有蛋糕,之后才会去关注其他事物,因此人眼机制具有局部相关性,每次都是看一部分,最后再把所有的事物综合在一起。
由于图像的空间联系是局部的,每个神经元不需要对全部的图像做感受,只需要感受局部特征即可,然后在更高层将这些感受得到的不同的局部神经元综合起来就可以得到全局的信息了,这样可以减少连接的数目。
参数共享

不同于以往的神经网络参数不共享的设定,卷积神经网络首次引入了参数共享这一思想,每一张输出的特征图都是通过一个共享参数的卷积核与图片卷积而来。在卷积神经网络中每个神经元连接数据窗的权重是固定的,每个神经元只关注一个特性。神经元就是图像处理中的滤波器,比如边缘检测专用的Sobel滤波器,即卷积层的每个滤波器都会有自己所关注一个图像特征,比如垂直边缘,水平边缘,颜色,纹理等等,这些所有神经元加起来就好比就是整张图像的特征提取器集合。
通过参数共享,使得原来的1.6MB参数降低为了60KB,网络的性能大大提高
CNN架构
卷积层----CONV
什么是卷积?
(1)卷积的定义
卷积实际上是两个信号的操作。
我们拿一维信号而言,两个一维时间信号的卷积f(t)*h(t)是这样定义的:

我们需要注意,两个一维时间信号的卷积f(t)*h(t),结果仍然是一个关于时间t的函数。
这和我们在信号处理里面接触的很多变换不同,这些变换的结果,和原来的信号往往不在一个域。例如,一个时间函数f(t)的傅里叶变换F(ω)是频域信号。
(2)卷积的数学意义
在卷积的定义式1.1中,等式右边的积分变量是τ。这样,h(t-τ)就是把h(τ)先按照纵轴对折,变成h(-τ)。
再将h(-τ)加一个时间上的偏移t。
然后把h(t-τ)同f(τ)相乘得到的函数在τ=[-∞,∞]覆盖的面积,就是得到了f(t)*h(t)。
注意,此时的这个面积,是对应某一个具体的t的时候卷积f(t)*h(t)的大小。
因为我们要得到所有的t时f(t)*h(t)的值,那么此时我们就需要去改变t。
对应的措施就是将t从-∞开始,沿着τ轴自左向右滑动。
每移动到一个新的位置t时,我们就计算这两个函数h(t-τ)和f(τ)的乘积函数的面积。这个面积就是卷积f(t)*h(t)在t处的值。
这个过程可以用图1.1来说明。

图示来解释卷积,其数学意义很清楚,但物理意义却模糊了。
(3)卷积的物理意义
经过上面对卷积的解释,读者可能觉得很奇怪,那么卷积的操作到底有什么用,为什么要进行卷积呢。通俗的讲。卷积核h(t)相当于一个滤波器,当两个函数进行卷积相当于它们频域相乘,滤波器把需要保留的频率部分保留下来(也就是图片特征),不需要的部分则滤除。因此通过卷积核与图像进行卷积可提取图像的特征图。
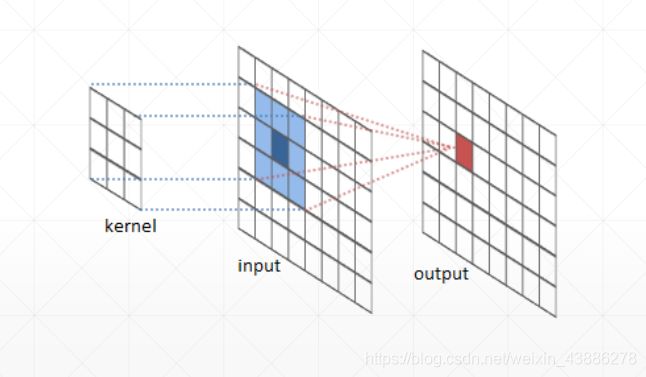
因为图像的像素值是离散而不是连续值,积分符号也就变形为点乘在相加,在二维中卷积操作定义为如下图所示

卷积核为3*3格式,与图片像素点一次点乘求和,得到一个输出。依次滑动卷积核与图像进行卷积,得到一个特征图。
经典卷积核举例
1.锐化

从卷积定义我们可以看出,处于卷积核中间的像素点减去四周像素点数值得到新生成特征图对应的输出。从直观上来理解,图片颜色一样的天空背景,由于颜色变化不大,可以看做进行操作的五个像素点数值相同,因此输出结果不变。对于图片中物体的轮廓分界处,中间像素点的值和四周不一致,进过上述操作后新得到的输出像素点和四周像素点差距会更加明显,因此上述卷积核起到了图片锐化的作用。放在频率中来讲,就相当于卷积核是一个高通滤波器,滤出了图片中的低频分量,使得图片中高频分量占比更多。
2.模糊

3.边缘检测

卷积层的操作
1.卷积运算
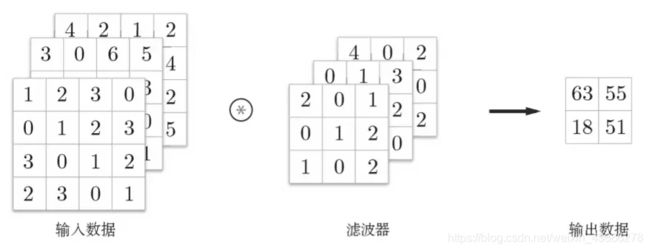
卷积层进行的处理就是卷积运算。下面举个例子:
本例中,输入大小是 (4, 4),滤波器大小是(3, 3),输出大小是(2, 2),滤波器在有的例子中也被成为卷积核。
对于输入数据,卷积运算以一定间隔滑动滤波器的窗口并应用。这里所 说的窗口是指图中灰色的3×3的部分。

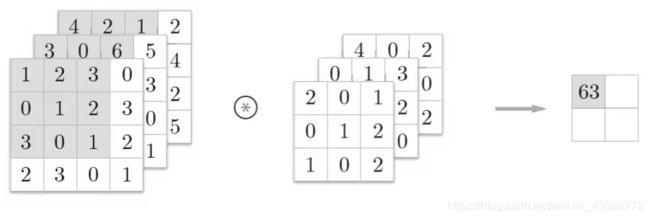
第一步
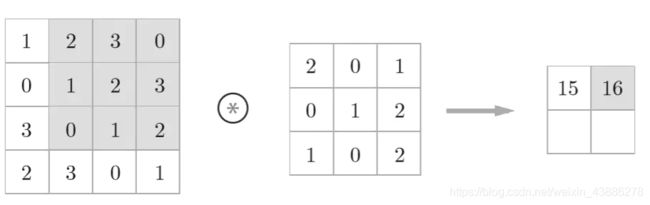
第二步

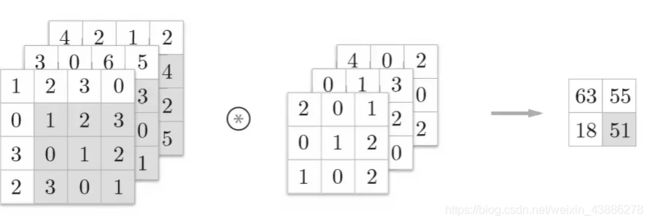
最后一步

在上述图中,滤波器中的参数对应于全连接层的参数,CNN中也有偏置,但偏置通常只有一个。
2.2填充
在进行卷积层的处理之前,有时要向输入数据的周围填入固定的数据(比 如0等),这称为填充(padding),是卷积运算中经常会用到的处理。
为什么要使用填充呢?使用填充主要是为了调整输出的大小。我们在每次进行卷积运算都会缩小空间,那么在某个时刻输出大小就有可能变为1,导致无法再应用卷积运算。为了避免出现这样的情况,就要使用填充。在刚才的例子中,将填充的幅度设为1,那么相对于输入大小(4, 4),输出大小也保持为原来的(4,4)。因此,卷积运算就可以在保持空间大小不变的情况下将数据传给下一层。
2.3步幅
应用滤波器的位置间隔称为步幅(stride)。下面是步幅为1和步幅为2的情况。
由2.2节和2.3节可知,增大步幅输出大小会变小,添加填充输出大小会变大。我们可以根据步幅和填充来计算输出大小。
假设输入大小为(H,W),滤波器大小为(FH,FW),输出大小为(OH,OW),填充为P,步幅为S。那么我们可以得到下面这个式子:

2.4三维数据的卷积运算
对于图像来说,图像是三维数据,除了高、长方向之外,还需要处理通道方向。在进行卷积运算时候,当通道方向上有多个特征图时,会按通道 进行输入数据和滤波器的卷积运算,并将结果相加,从而得到输出。
我们需要注意的是,在三维的卷积运算中,输入数据和过滤器的通道数要保持一致。
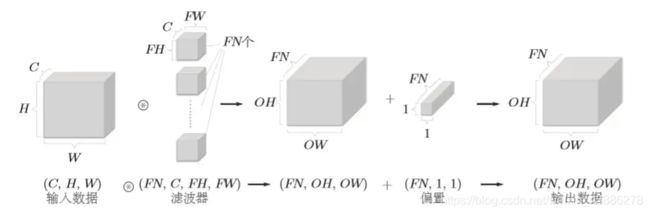
我们可以把上述例子中的输入数据和过滤器当成长方体方块来考虑。把3维数据表示为多维数组时,书写顺序为(channel,height,width)。比如,通道数为C、高度为H、长度为W的数据的形状可以写成(C, H,W)。滤波器也一样,要按(channel,height,width)的顺序书写。比如,通道数为C、滤波器高度为FH(Filter Height)、长度为FW(Filter Width)时,可以写成(C,FH,FW)。
如果我们要在通道方向上有多个卷积运算的输出,我们应该这样做,即用到多个滤波器。用图片表示如下:
当考虑到滤波器的数量时,那么数据就变成了4维数据,滤波器的权重数据要按(output_channel,input_channel,height,width)的顺序书写。
在上图中,每个通道只有一个偏置。这里,偏置的形状是(FN,1,1), 滤波器的输出结果的形状是(FN,OH,OW)。这两个方块相加时,要对滤波 器的输出结果(FN,OH,OW)按通道加上相同的偏置值。另外,不同形状的 方块相加时,可以基于NumPy的广播功能轻松实现。
2.5卷积运算中的批处理
我们在卷积层进行批处理时,需要将在各层间传递的数据保存为4维数据。具体地讲,就是按(batch_num,channel,height,width)的顺序保存数据。
上图批处理版的数据流中,在各个数据的开头添加了批用的维度。数据作为4维的形状在各层间传递。批处理中网络间传递的是4维数据,将N个数据进行打包处理,将N卷积运算汇成了一次卷积运算。
池化层----POOL
池化层夹在连续的卷积层中间, 用于压缩数据和参数的量,减小过拟合。
简而言之,如果输入是图像的话,那么池化层的最主要作用就是压缩图像。
这里再展开叙述池化层的具体作用。
1.特征不变性,也就是我们在图像处理中经常提到的特征的尺度不变性,池化操作就是图像的resize,平时一张狗的图像被缩小了一倍我们还能认出这是一张狗的照片,这说明这张图像中仍保留着狗最重要的特征,我们一看就能判断图像中画的是一只狗,图像压缩时去掉的信息只是一些无关紧要的信息,而留下的信息则是具有尺度不变性的特征,是最能表达图像的特征。
2.特征降维,我们知道一幅图像含有的信息是很大的,特征也很多,但是有些信息对于我们做图像任务时没有太多用途或者有重复,我们可以把这类冗余信息去除,把最重要的特征抽取出来,这也是池化操作的一大作用。
3.在一定程度上防止过拟合,更方便优化。
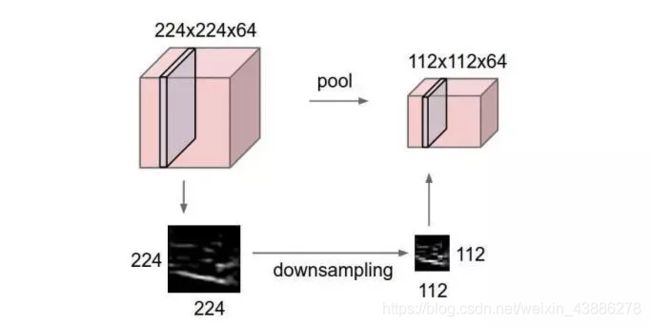
池化层用的方法有Max pooling 和 average pooling,而实际用的较多的是Max pooling。
这里就说一下Max pooling,其实思想非常简单。

对于每个2 * 2的窗口选出最大的数作为输出矩阵的相应元素的值,比如输入矩阵第一个2 * 2窗口中最大的数是6,那么输出矩阵的第一个元素就是6,如此类推。

虽然人不太容易分辨出池化后的特征图,但是没关系,机器还是可以识别的。