机器学习(三)KNN回归
基于KNN 算法,实现对于鸢尾花第四个数据的预测
原理
该算法用于回归预测,根据前三个特征属性,寻找最近的k个邻居,然后再根据k个邻居的第4个特征属性,去预测当前样本的第4个特征值
数据集的准备和处理
- 删除数据中不需要的类别列和重复的数据
data = pd.read_csv(r"iris.arff.csv", header=0)
#删除不需要class列(特征), 因为进行回归预测 ,类别信息,没有用处了
data.drop(["class"],axis = 1, inplace = True)
#删除重复的记录
data.drop_duplicates(inplace = True)
data
- 将数据集打乱并分为训练集和测试集
t = data.sample(len(data),random_state = 0)
train_X = t.iloc[:120,:-1]
train_y = t.iloc[:120,-1]
test_X = t.iloc[120:,:-1]
test_y = t.iloc[120:,-1]
KNN类的实现
class KNN:
'''使用Python实现K近邻算法(回归预测)
该算法用于回归预测,根据前三个特征属性,寻找最近的k个邻居,然后再根据k个邻居的第4个特征
属性,去预测当前样本的第4个特征值
'''
def __init__(self,k):
'''初始化方法
Parameters
-----
k:int
邻居个位数
'''
self.k = k
def fit(self, X, y):
'''训练方法
Parameeters
-----
X: 类数组类型(特征矩阵),可以是List也可以是Ndarray,形状为: [样本数量,特征数量]
待训练的样本特征(属性)
y: 类数组类型,形状为:[样本数量]
每个样本的目标值(标签)
'''
#将X,y转换为ndarray类型
self.X = np.asarray(X)
self.y = np.asarray(y)
def predict(self, X):
'''根据参数传递的样本,对样本数据进行预测
Parameters:
-----
X: 类数组类型,可以是List也可以是Ndarray,形状为: [样本数量,特征数量]
待测试的样本特征(属性)
Returns:
-----
result :
数组类型,预测结果
'''
#转换为数组类型
X = np.asarray(X)
#保存预测的结果值
result = []
#对ndarray数组进行遍历,每次取数组中的一行
for x in X:
#计算距离 (计算与训练集中每个X的距离)
dis = np.sqrt(np.sum((x - self.X) ** 2, axis = 1))
#返回排序后,每个元素在原数组(排序之前的数组) 中的索引
index = dis.argsort()
#进行截取,只取前k个元素 (取距离最近的k个元素的索引)
index = index[:self.k]
#计算均值,然后加入到结果列表当中。
result.append(np.mean(self.y[index]))
return np.array(result)
显示预测结果并与测试值对比
knn = KNN(k = 3)
knn.fit(train_X,train_y)
result = knn.predict(test_X)
display(result)
np.mean(np.sum((result - test_y) ** 2))
display(test_y.values)
array([1.33333333, 2. , 1.2 , 1.26666667, 1.93333333,
1.16666667, 2.16666667, 0.36666667, 1.9 , 1.4 ,
1.2 , 0.16666667, 1.93333333, 2.26666667, 1.73333333,
0.13333333, 1.03333333, 1.3 , 1.83333333, 1.23333333,
0.16666667, 0.23333333, 0.16666667, 2.03333333, 1.2 ,
1.8 , 0.2 ])
array([1.5, 1.8, 1. , 1.3, 2.1, 1.2, 2.2, 0.2, 2.3, 1.3, 1. , 0.2, 1.6,
2.1, 2.3, 0.3, 1. , 1.2, 1.5, 1.3, 0.2, 0.4, 0.1, 2.1, 1.1, 1.5,
0.2])
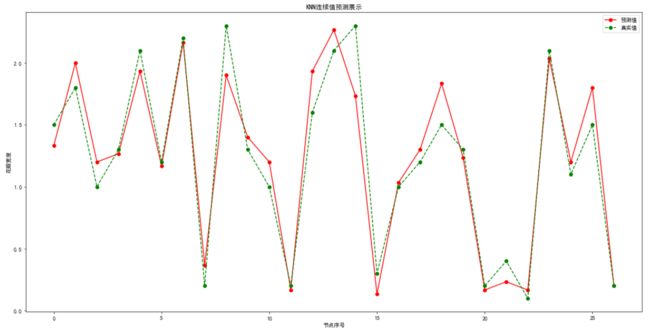
预测结果可视化展示
#预测结果可视化展示
import matplotlib as mpl
import matplotlib.pyplot as plt
#设置画布的大小
plt.figure(figsize=(20,10))
#默认情况下,matplotlib不支持中文显示,设置支持中文
#设置字体为黑体,以支持中文显示
mpl.rcParams["font.family"] = "SimHei"
#设置在中文字体时,能够正常的显示负号(-)
mpl.rcParams["axes.unicode_minus"] = False
#绘制预测值
plt.plot(result,"ro-",label = "预测值")
#绘制真实值
plt.plot(test_y.values,"go--",label = "真实值")
#设置折线图参数
plt.title("KNN连续值预测展示")
plt.xlabel("节点序号")
plt.ylabel("花瓣宽度")
plt.legend()
plt.show()
样本预测加入权重计算
- 权重计算公式
w = 该 节 点 距 离 的 倒 数 所 有 K 邻 近 节 点 距 离 的 的 倒 数 和 w = \frac {该节点距离的倒数} {所有K邻近节点距离的的倒数和} w=所有K邻近节点距离的的倒数和该节点距离的倒数
- 权重均值公式
c = w 1 ⋅ y 1 + w 2 ⋅ y 2 + . . . + w k ⋅ y k c = w_1 ·y_1 + w_2 · y_2 + ...+w_k · y_k c=w1⋅y1+w2⋅y2+...+wk⋅yk
- 对KNN类中的predict进行改写
def predict2(self, X):
'''根据参数传递的样本,对样本数据进行预测(考虑权重)
权重计算方式:使用每个节点(邻居)距离的倒数 /所有节点(邻居)距离的倒数之和
Parameters:
-----
X: 类数组类型,可以是List也可以是Ndarray,形状为: [样本数量,特征数量]
待测试的样本特征(属性)
Returns:
-----
result :
数组类型,预测结果
'''
#转换为数组类型
X = np.asarray(X)
#保存预测的结果值
result = []
#对ndarray数组进行遍历,每次取数组中的一行
for x in X:
#计算距离 (计算与训练集中每个X的距离)
dis = np.sqrt(np.sum((x - self.X) ** 2, axis = 1))
#返回排序后,每个元素在原数组(排序之前的数组) 中的索引
index = dis.argsort()
#进行截取,只取前k个元素 (取距离最近的k个元素的索引)
index = index[:self.k]
#求所有邻居节点的倒数之和
s = np.sum(1 / dis[index] + 0.001) #最后加上一个很小的值(0.001),为了避免除数为0的情况
#求每个节点的权重 (每个节点的倒数 / 倒数之和 得到权重)
weight = 1 / (dis[index] + 0.001) / s
#计算权重均值,然后加入到结果列表当中。
result.append(np.sum(self.y[index] * weight))
return np.array(result)