KL散度和交叉熵

本文主要包括：
$1.kl散度和交叉熵的概念比较$
$2.交叉熵在分类任务中的本质$

在学习机器学习的过程中，我们经常会碰到这两个概念：KL散度（kl divergence）以及交叉熵，并且经常是同时出现的。很多同学对这两个概念都理解的不是很透彻，造成经常会搞混他们两者。本文最主要的目的就是带大家深入理解这两个重要的概念，同时搞懂，区别的理解他们，保证以后不会再搞混它们。
首先，这两个概念都来自信息论。
交叉熵：当我们使用模型Q来编码（表示）来自分布P的数据时，所需要的平均bit数。
交叉熵数学定义为：
$H(p,q)=-{\sum }_{i=1}^{n}p(x_i)log(q(x_i))$

KL散度： 也就是相对熵, 是当我们使用模型（分布）Q来编码，而不是使用真实的P分布来编码数据时，额外需要的平均bit数。（重点在“额外”，也就是“相对”----交叉熵相对熵额外的那部分熵，就是KL散度）
KL散度的数学定义为：
$D_{KL}(p||q)={\sum }_{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i})$
对KL散度数学定义进行分解：

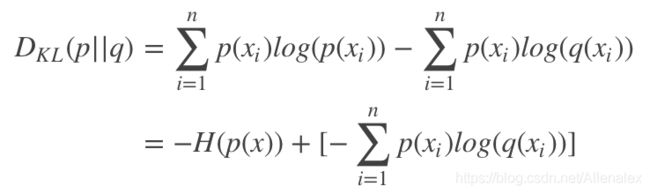
等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵。可以看出，交叉熵减去熵等于KL散度。也就是，交叉熵是，如果用q代替p产生x, 得到的熵，而相对熵，是相对用自身概率p，而新增的那部分信息（熵）。

其中，在分类任务中， 熵这一项，就是分类类别的熵，这个值为0（因为一条记录的label是确定属于某个类别的，也就是没有任何信息可言，熵就是0，或者说，指定的那个类别为1，其他为0，通过熵的计算公式也可以知道，熵为0），所以，在分类任务中，最小化KL散度和最小化交叉熵是一样的（实际上，我们在分类任务中，常用的就是交叉熵）

接下来我们来探究下交叉熵在分类预测中的本质。也就是说，在分类中，交叉熵损失为0的模型是完美的模型，那>0的交叉熵究竟意味着什么呢？怎么理解交叉熵损失不同的取值？
下面这段代码可以看下，从分布完全匹配到两个分布完全相反，这过程中的交叉熵变化。

# cross-entropy for predicted probability distribution vs label
from math import log
from matplotlib import pyplot

# calculate cross-entropy
def cross_entropy(p, q, ets=1e-15):
	return -sum([p[i]*log(q[i]+ets) for i in range(len(p))])

# define the target distribution for two events
target = [0.0, 1.0]
# define probabilities for the first event
probs = [1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.0]
# create probability distributions for the two events
dists = [[1.0 - p, p] for p in probs]
# calculate cross-entropy for each distribution
ents = [cross_entropy(target, d) for d in dists]
# plot probability distribution vs cross-entropy
pyplot.plot([1-p for p in probs], ents, marker='.')
pyplot.title('Probability Distribution vs Cross-Entropy')
pyplot.xticks([1-p for p in probs], ['[%.1f,%.1f]'%(d[0],d[1]) for d in dists], rotation=70)
pyplot.subplots_adjust(bottom=0.2)
pyplot.xlabel('Probability Distribution')
pyplot.ylabel('Cross-Entropy (nats)')
pyplot.show()

输出的图最终如下所示：

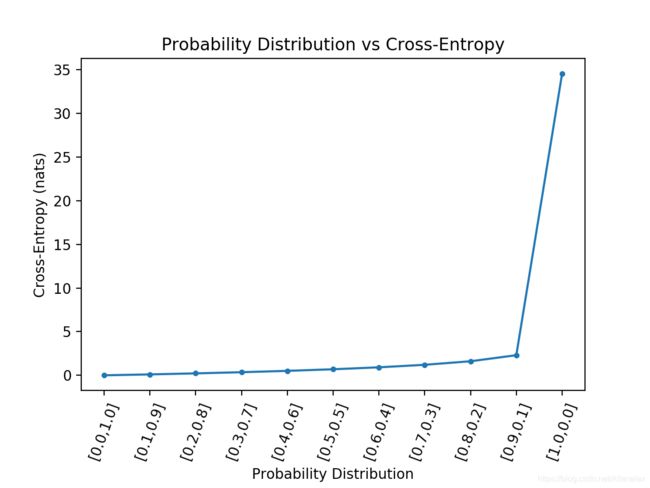
就像预期的那样，当预测的概率分布和目标分布完全匹配的时候，交叉熵是为0的，随着分布差别越来越大，交叉熵也是平稳增加的。只要当分布完全相反是，交叉熵才会飙升很大。当然，在实际的分类任务中，肯定是不会出现这样跟实际分布完全相反的分布的。如果把这种极端完全相反的去掉，代码如下：

# cross-entropy for predicted probability distribution vs label
from math import log
from matplotlib import pyplot

# calculate cross-entropy
def cross_entropy(p, q, ets=1e-15):
	return -sum([p[i]*log(q[i]+ets) for i in range(len(p))])

# define the target distribution for two events
target = [0.0, 1.0]
# define probabilities for the first event
probs = [1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1]
# create probability distributions for the two events
dists = [[1.0 - p, p] for p in probs]
# calculate cross-entropy for each distribution
ents = [cross_entropy(target, d) for d in dists]
# plot probability distribution vs cross-entropy
pyplot.plot([1-p for p in probs], ents, marker='.')
pyplot.title('Probability Distribution vs Cross-Entropy')
pyplot.xticks([1-p for p in probs], ['[%.1f,%.1f]'%(d[0],d[1]) for d in dists], rotation=70)
pyplot.subplots_adjust(bottom=0.2)
pyplot.xlabel('Probability Distribution')
pyplot.ylabel('Cross-Entropy (nats)')
pyplot.show()

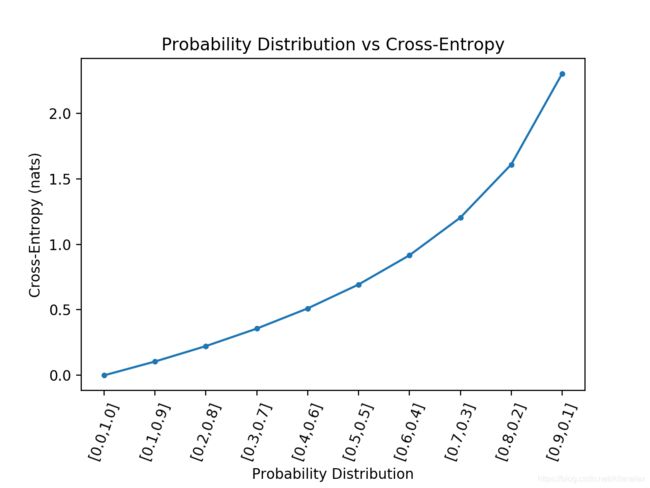
从以上的结果我们可以回答以下问题： 多大的交叉熵分值才是好的分值？
如果是使用的是nat (以e为底的log), 平均交叉熵低于0.2就不错。小于0.1或者0.05就更加的好了。否则，如果得到的交叉熵大于0.2或者0.3，你还可以继续优化；如果你得到的交叉熵要大于1了，那说明你肯定在很多的样本上的预测的概率非常的差。
总结如下：
Cross-Entropy = 0.00: Perfect probabilities.
Cross-Entropy < 0.02: Great probabilities.
Cross-Entropy < 0.05: On the right track.
Cross-Entropy < 0.20: Fine.
Cross-Entropy > 0.30: Not great.
Cross-Entropy > 1.00: Terrible.
Cross-Entropy > 2.00 Something is broken.
熟悉这个，能够帮助你很好的解释你的LR或者神经网络模型的交叉熵损失。
你还可以给每个类分开计算交叉熵，这样你能够看下你的模型在每个类上的表现。

参考资料

[1]: https://machinelearningmastery.com/cross-entropy-for-machine-learning/
[2]:https://machinelearningmastery.com/divergence-between-probability-distributions/