【学时总结】 ◆学时 · 一◆ A*算法
【学时·一】A*算法
■基本策略■
——A*(A Star)无非就是BFS的升级,当BFS都超时的时候……
同样以队列为基础结构,BFS使用FIFO队列(queue),而A*则使用优先队列(priority_queue)。与BFS的优化极其相似,但一般的BFS优化只是相当于使用了一个最优性剪枝,偶尔不会起到足够的优化所以就TLE了。
所以A*算法改进了其优先级的判定方法,使用了一个启发函数(没错,就是这么水的名字),它可以“乐观”地预估出一个从当前状态到达目标状态的代价,且此预估值必然小于等于实际值,否则A*算法就会出错。
■一般的搜索题■
这是A*的解题范围和其他搜索算法可以实现的解题范围的重叠域
◆永恒的经典◆ 八数码问题
· 以下引用自POJ 1077
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 x
where the only legal operation is to exchange ‘x’ with one of the tiles with which it shares an edge. As an example, the following sequence of moves solves a slightly scrambled puzzle:
1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
5 6 7 8 5 6 7 8 5 6 7 8 5 6 7 8
9 x 10 12 9 10 x 12 9 10 11 12 9 10 11 12
13 14 11 15 13 14 11 15 13 14 x 15 13 14 15 x
r-> d-> r->
The letters in the previous row indicate which neighbor of the ‘x’ tile is swapped with the ‘x’ tile at each step; legal values are ‘r’,’l’,’u’ and ‘d’, for right, left, up, and down, respectively.
Not all puzzles can be solved; in 1870, a man named Sam Loyd was famous for distributing an unsolvable version of the puzzle, and frustrating many people. In fact, all you have to do to make a regular puzzle into an unsolvable one is to swap two tiles (not counting the missing ‘x’ tile, of course).
In this problem, you will write a program for solving the less well-known 8-puzzle, composed of tiles on a three by three arrangement.
· 解析
这道题显然是一道搜索题,不过有一点变形……就难了许多。当然,这道题用BFS或者双向BFS能过,但是A*算法实际运行时间更优。
1.启发函数
作为整个A*算法的精华,这个函数显得十分重要,那么下面给出2个思路:
思路A: H()-当前状态有多少个元素不在正确位置; G()-当前搜索的深度,即用了的操作数; 最后一次操作将会在一次操作中将2个元素归位,所以启发函数 F()=H()−1+G() F ( ) = H ( ) − 1 + G ( ) ;
评价: 这个启发函数一定正确,但是通常与真实值相差过大,不是特别优;
思路B: H()-当前状态中位置不对的元素(不包含空位子)与正确位置的曼哈顿距离之和; G()-当前搜索的深度,即用了的操作数; 由于将一个元素归位至少需要H()次操作;
评价: 估测值与真实值较为接近,且不会超过真实值;
2.优先队列的定义
优先队列是A*算法所依赖的数据结构。STL的priority_queue能够实现自动排序,但有一个缺点——当需要输出路径时,STL的队列并没有提供访问删除了的元素的函数,因此无法通过记录“父亲”状态来输出路径,这时候就需要手写优先队列……QwQ
现在暂时不考虑这种尴尬情况,就当是只输出最短方案操作次数。那么我们需要一个结构体:
struct Node
{
int pri,code,whe,dep;
//优先级H(),八数码数字表示,空位的位置,搜索深度
}
bool operator <(Node A,Node B) {return A.pri+A.dep>B.pri+B.dep;}这样定义了优先级过后就可以利用STL直接排序了~
3.如果代码不懂可以看这篇Blog:
Eight 八数码问题
· 源代码
仅供参考,如有不足(我知道写得复杂了点)请评论指出
/*Lucky_Glass*/
#includeif(vis[m][i]==n)
return true;
vis[m].push_back(n);
return false;
}
int main()
{
// freopen("in.txt","r",stdin);
priority_queue que;
for(int i=0,j=0;i<9;i++)
{
scanf("%d",&num[j]);
Push.code=Push.code*10+num[j];
if(num[j]) j++;
else Push.whe=i+1;
}
int End=0;
for(int i=0,x;i<9;i++)
scanf("%d",&x),End=10*End+x;
Push.pri=H(Push.code);
que.push(Push);
while(!que.empty())
{
Node Top=que.top();que.pop();
for(int i=0;i<4;i++)
{
Push=Top;
Push.whe+=MOve[i];Push.dep++;
if(Push.whe<=0 || Push.whe>9 || (i%2 && (Push.whe-1)/3!=(Top.whe-1)/3)) continue;
Push.code=(int)change(Push.code,Push.whe,Top.whe);
if(Find(Push.code)) continue;
if(Push.code==End)
{
printf("%d",Push.dep);
return 0;
}
Push.pri=H(Push.code);
que.push(Push);
}
}
puts("-1");
return 0;
} ◆真正的难题◆ 15数码问题
BFS真的过不了了……
UVA 15-Puzzle Problem
· 解析
这两道题唯一的区别就是数据规模,8数码的可能情况不超过 9! 9 ! 种,但是15数码的可能情况是在 16! 16 ! 种以内!所以只加上一般的判重并不能起到什么优秀的作用,所以用到了A*算法,启发函数和原来一样。但是……
人无完人,A*算法也是有缺陷的 QwQ
正如双向BFS,A*算法虽然在一般情况下较快,而这一般情况就是有解的情况。如果无解,双向搜索会退化为两个不相交的圆,既浪费空间又浪费时间;而A*算法会退化为普通的BFS(需要搜索完所有解),且比普通BFS慢——每次插入的时间复杂度为 O(logsiz) O ( log s i z ) 。15数码仍然有无解的情况,所以为了避免超时(枚举出所有情况肯定会超时啊),我们需要预判:
bool If_ans(int brd[][4])
{
int sum=0,siz=0,x,y,tmp[17]={};
for(int i=0;i<4;i++)
for(int j=0;j<4;j++)
{
tmp[siz++]=brd[i][j];
if(!brd[i][j]) x=i,y=j;
}
for(int i=0;i<16;i++)
for(int j=i+1;j<16;j++)
if(tmp[j]if((sum+x)%2==0) return false;
return true;
} 上面这段代码的意思就是——将4*4的15数码矩阵除去0后,每行相接形成一个链状表(tmp),求出逆序对的个数(sum),如果加上0的行数(行数从0开始)的和是二的倍数,则无解,否则有解。其实就是下面这样:

最为权威的英文证明:Workshop Java - Solvability of the Tiles Game
· 源代码
这段代码并不算优秀,实际上利用了 Uva 的数据漏洞,真正的解是 IDA*,之后再说
/*Lucky_Glass*/
#includeif((sum+x)%2==0) return false;
return true;
}
bool A_Star(state srt)
{
priority_queue que;
state Top,Pus;
que.push(srt);
while(!que.empty())
{
Top=que.top();que.pop();
for(int i=0;i<4;i++)
{
Pus=Top;Pus.x+=mov[i][0];Pus.y+=mov[i][1];
if(Pus.x<0 || Pus.x>3 || Pus.y<0 || Pus.y>3) continue;
swap(Pus.brd[Pus.x][Pus.y],Pus.brd[Top.x][Top.y]);
Pus.dep++;
if(Pus.dep>50) continue;
Pus.ans+=chr[i];Pus.pri=Get_pri(Pus.brd);
if(!Pus.pri) {cout<return true;}
if(Pus.ans.size()>=2)
{
int f1=Pus.ans.size()-1,f2=Pus.ans.size()-2;
if((Pus.ans[f1]=='U' && Pus.ans[f2]=='D') || (Pus.ans[f1]=='D' && Pus.ans[f2]=='U') || (Pus.ans[f1]=='L' && Pus.ans[f2]=='R') || (Pus.ans[f1]=='R' && Pus.ans[f2]=='L'))
continue;
}
que.push(Pus);
}
}
return false;
}
int main()
{
int t;scanf("%d",&t);
while(t--)
{
state srt;
for(int i=0;i<4;i++)
for(int j=0;j<4;j++)
{
scanf("%d",&srt.brd[i][j]);
if(!srt.brd[i][j]) srt.x=i,srt.y=j;
}
if(!If_ans(srt.brd))
{
printf("This puzzle is not solvable.\n");
continue;
}
srt.dep=0;srt.pri=0;
if(!A_Star(srt)) printf("This puzzle is not solvable.\n");
}
return 0;
} ■k-短路问题■
其他的搜索拿这个题型没辙了 (`・ω・´)
◆一道版题◆ k-th shortest POJ 2449
(题目长在超链接里)
· 解析
其实就是标准的k短路。如果是一般的搜索肯定会TLE的,那么为什么A*可以完成呢?原因如下:
1. A*算法利用优先队列,所以它按顺序找到的第k条路径一定是第k短的路径;
2. 它最高的时间复杂度仅比BFS多 O(logsiz) O ( log s i z ) ,所以时间复杂度并不高;
3. 我们可以通过k次最短的路径查找只进行一次BFS;
与之前的算法不同,我们在原来的A*算法中会有判重,并舍弃优先级低的情况;但是由于K短路中,同一条路径可能走多次,以达到第k短的路径。比如下面:
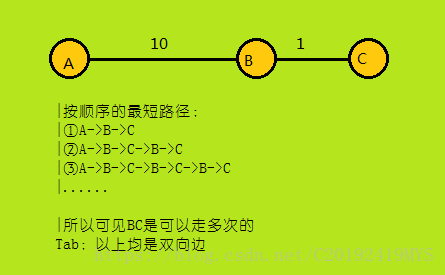
但是这样也造成了一些麻烦,有时候是无解的:
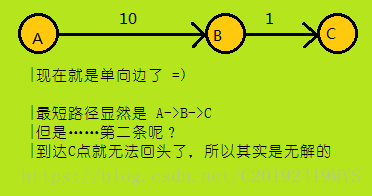
然后回到A*算法——由于我们按优先级排序,所以我们当前的队头元素一定是现在整个队列中最优的情况(前提是启发函数写对了);所以当我们第n次搜索到终点时,当前的路径就是第n短路径,为了避免意外,我们还可以先把到达终点的情况push到队列里,当整个操作完毕再次以到达终点的情况为队头时,说明它的确是第n短的。
根据这一性质,我们可以在队头元素是终点时,记录是第几次访问到终点,如果恰好是第n次,则返回答案——注意:此时虽然访问到终点,但还要把这种情况push进队列,否则反例见上图。
别急着写代码,有一个小坑。由于我们是判断队头是否为终点,所以当起点终点重合时,按题意应该不算最短路径,但当程序进入BFS时会记录一次。所以我们给出特判——当起点终点重合时,k++。
·源代码
/*Lucky_Glass*/
#includeelse return cmp.privector lec[POI+5],dis_lec[POI+5];
int n_poi,n_edg,srt,fin,kth,INF;
int dis[POI+5];
inline Line Make_Line(int v,int l){return Line{v,l};};
void SPFA()
{
bool vis[POI+5]={};
memset(dis,0x3f,sizeof dis);INF=dis[0];
queue<int> que;
dis[fin]=0;que.push(fin);
while(!que.empty())
{
int Fro=que.front();que.pop();
vis[Fro]=false;
for(int i=0;iint Pus=dis_lec[Fro][i].v;
if(dis[Pus]>dis[Fro]+dis_lec[Fro][i].len)
{
dis[Pus]=dis[Fro]+dis_lec[Fro][i].len;
if(!vis[Pus]) que.push(Pus),vis[Pus]=true;
}
}
}
}
int A_Star()
{
if(srt==fin) kth++;
if(dis[srt]==INF) return -1;
priority_queue que;
que.push(state{srt,0,dis[srt]});
int tot=0;
while(!que.empty())
{
state Top=que.top();que.pop();
if(Top.u==fin)
{
tot++;
if(tot==kth) return Top.dep;
}
for(int i=0;ireturn -1;
}
int main()
{
scanf("%d%d",&n_poi,&n_edg);
for(int i=0,u,v,l;iscanf("%d%d%d",&u,&v,&l),lec[u].push_back(Line{v,l}),dis_lec[v].push_back(Line{u,l});
scanf("%d%d%d",&srt,&fin,&kth);
SPFA();
printf("%d\n",A_Star());
return 0;
} The End T h e E n d
Thanks for reading! T h a n k s f o r r e a d i n g !
− Lucky_Glass − L u c k y _ G l a s s