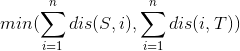牛客多校第六场 G Pikachu（树形dp）

链接：https://www.nowcoder.com/acm/contest/144/G
来源：牛客网
 

题目描述

In Viridian forest there is a tree T formed by N nodes, each edge on which has a positive weight.

There is an undirected graph G generated from tree T, which contains N nodes and undirected edges, where the capacity of the edge between u and v equals to the distance between them on the tree T.

Given the tree T, Pikachu wants to calculate the sum of the max flow between every two nodes in G, there are different pairs of nodes should be counted. Could you help him?

输入描述:

The input starts with one line containing exactly one integer t, which is the number of test cases.

For each test case, the first line contains one integer N, indicating the size of the tree T.

Then followed by N - 1 lines, each consists of three integers ui, vi and wi, representing the two nodes connected by the i-th edge and the weight of the i-th edge.

- 1 ≤ t ≤ 10.
- 2 ≤ N ≤ 105.
- 1 ≤ wi ≤ 1000.
- 

输出描述:

For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the sum of the maximum flow between every two nodes in G.

示例1

输入

复制

2
3
1 2 1
2 3 1
5
1 2 1
2 3 1
2 4 1
4 5 2

输出

复制

Case #1: 7
Case #2: 72

题目大意：现在给出一棵树，树上的边有权值。现在构造一个完全图，任意两点u,v之间的流量为树上u,v的距离，现在要求出图上任意两点的最小割之和。

题目思路：如果在一个图中给定源点S和汇点T，那么这两点之间的割为

,为两点之间的流量，即树上为两点的距离。

因为要求的是最小割，相当于选择一种结点染色方案，使得S结点是白色的，T结点是黑色的，图上同色的结点距离和最大。

显然只有除S和T以外所有点与S同色或者与T同色时，这个距离和最大，所以S到T的最小割为

。

这样我们就可以通过树形dp维护出任意一个点到其它所有点的距离之和。

对于一棵树，第一次dfs的过程我们考虑计算每条边的贡献，可以求出一个结点到它的所有子节点的距离之和，做第二次dfs的时候再将父亲结点的贡献加到子节点上，即可求出一个结点到其它结点的距离之和了。

求完再对结果进行排序，每个结点的距离之和对答案的贡献为（即第 i 小的值对答案贡献了n-i次）。

这题数据较大，会爆unsigned long long，所以可以考虑用JAVA大数或者__int128。

具体实现看代码：

#include 
#define fi first
#define se second
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define lowbit(x) x&-x
#define pb push_back
#define MP make_pair
#define clr(a) memset(a,0,sizeof(a))
#define _INF(a) memset(a,0x3f,sizeof(a))
#define FIN freopen("in.txt","r",stdin)
#define fuck(x) cout<<"["<pii;
typedef pairpll;
typedef vector VI;
const int MX=1e5+7;
const int mod=998244353;
const int inf=0x3f3f3f3f;

int n,_,sz[MX];
vectorE[MX];
_int dis[MX];

void dfs(int u,int fa){
	sz[u]=1;dis[u]=0;
	for(auto nw:E[u]){
		int v=nw.fi,w=nw.se;
		if(v==fa) continue;
		dfs(v,u);
		sz[u]+=sz[v];
		dis[u]+=dis[v]+(_int)w*sz[v];
	}
}
void DFS(int u,int fa){
	for(auto nw:E[u]){
		int v=nw.fi,w=nw.se;
		if(v==fa) continue;
		dis[v]+=dis[u]-dis[v]-(_int)w*sz[v]+(_int)(n-sz[v])*w;
		DFS(v,u);
	}
}

void Print(_int x){
	if (x == 0) {
        printf ("0\n");
        return;
    }
    vectorver;
    while (x) ver.push_back (x % 10), x /= 10;
    reverse (ver.begin(), ver.end() );
    for (auto i:ver) printf ("%d", i);
    printf("\n");
}

int main(){
	//FIN;
	int cas=0;
	for(scanf("%d",&_);_;_--){
		scanf("%d",&n);
		for(int i=1;i<=n;i++) E[i].clear();
		for(int i=1;i