二维卷积神经网络的初始化为0及其他初始化方式对比

今天想结合实验及公式讨论下，二维卷积神经网络下，

• 初始化为0
• 初始化为常数
• kaiming初始化

3种初始化方式的结果。
并分析复杂模型不能初始化为0的根本原因。

1. 实验背景

先介绍下实验模型，用的是Pytorch下两层卷积网络，各接BN层和ReLU层：

class Model(nn.Module):
	def __init__(self):
		super(Model, self).__init__()
		self.conv1 = nn.Conv2d(3, 3, 3, padding=1, bias=False)
		self.bn1 = nn.BatchNorm2d(3)
		self.conv2 = nn.Conv2d(3, 3, 3, padding=1, bias=False)
		self.bn2 = nn.BatchNorm2d(3)
		self.relu = nn.ReLU(inplace=True)

		for m in self.modules():
			if isinstance(m, nn.Conv2d):
				nn.init.constant_(m.weight, 0.)

		# for m in self.modules():
		# 	if isinstance(m, nn.Conv2d):
		# 		nn.init.constant_(m.weight, 5.)
	
		# for m in self.modules():
		# 	if isinstance(m, nn.Conv2d):
		# 		nn.init.kaiming_normal_(m.weight, mode="fan_in", nonlinearity="relu")

	def forward(self, x):
		x = self.conv1(x)
		x = self.bn1(x)
		x = self.relu(x)
		x = self.conv2(x)
		x = self.bn2(x)
		x = self.relu(x)
		return x

优化器选用SGD+momentum，学习率为1e-2

optimizer = torch.optim.SGD(params=model.parameters(), lr=1e-2)

训练40个epoch观察loss、两个conv层的均值和方差。

2. 实验结果

老规矩，先上结果！

下面分别为4个实验的结果：

• 初始化为0
• 初始化为0但只有一个conv层
• 初始化为5
• kaiming初始化

每个实验结果中的5个折线图分别为：

• loss值
• conv1的均值
• conv1的方差
• conv2的均值
• conv2的方差

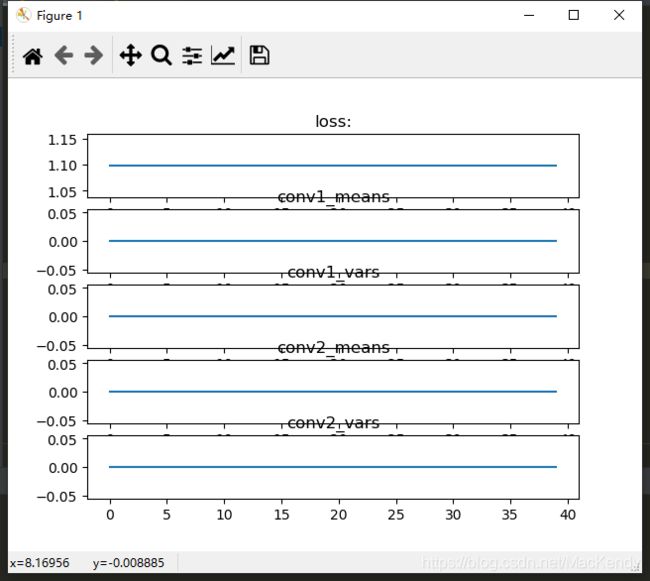
初始化为0：

for m in self.modules():
	if isinstance(m, nn.Conv2d):
		nn.init.constant_(m.weight, 0.)

观察到经过40个epoch，两个conv层的均值和方差一直保持为0。
loss也一直悬浮在1.10附近。

初始化为0且只留一个conv层：

for m in self.modules():
	if isinstance(m, nn.Conv2d):
		nn.init.constant_(m.weight, 0.)

在forward处把其他层都注释掉：

	def forward(self, x):
		# x = self.conv1(x)
		# x = self.bn1(x)
		# x = self.relu(x)
		x = self.conv2(x)
		# x = self.bn2(x)
		# x = self.relu(x)
		return x

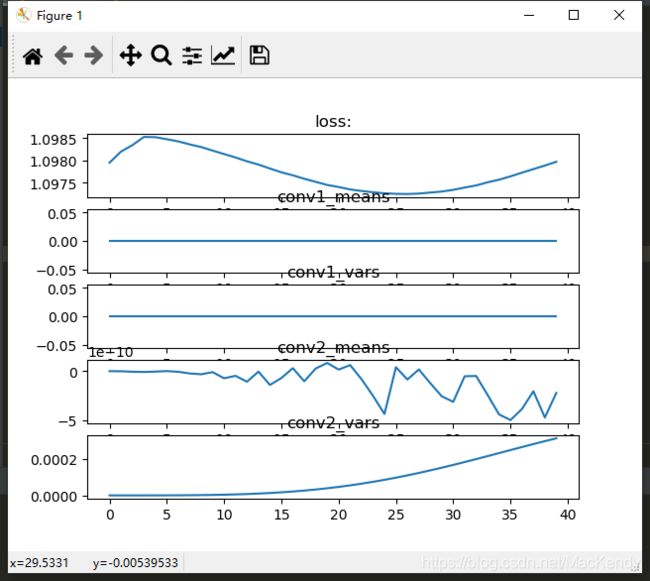
可以看到虽初始化为0，但在只剩一个conv层的时候，是能产生梯度的。（后面会通过公式解释）

初始化为5：

for m in self.modules():
	if isinstance(m, nn.Conv2d):
		nn.init.constant_(m.weight, 5.)

初始化为5是可以通过SGD跑起来的，两个conv层的方差随着训练的迭代在提升，均值在5附近震荡。

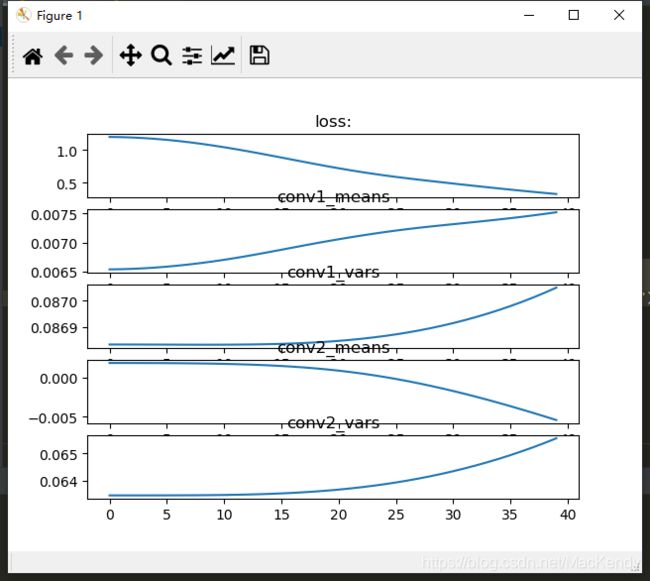
kaiming初始化：

for m in self.modules():
	if isinstance(m, nn.Conv2d):
		nn.init.kaiming_normal_(m.weight, mode="fan_in", nonlinearity="relu")

明显观察到两个conv层的学习是很平缓的。

对比 初始化为0 和 初始化为0且只留一个conv层 可以得知，单层卷积初始化为0是可以产生梯度的，但在两层及以上的卷积网络初始化为0则梯度均为0。
对比 初始化为0 和 初始化为5 ，在相同的网络结构下，后者是能够训练起来的（抛开训练的好坏），证明初始化为常数不是训练失败的根本原因，初始化为0才是。
对比 初始化为5 和 kaiming初始化 ，在相同的网络结构、相同的训练次数下，后者的loss值更低，证明在加了BN层后，科学的初始化方式，仍能有效提升模型的训练速度。

3. 公式推导

此处仅展示一层conv的计算过程，足以解释多层卷积网络初始化为0的致命影响。

假设图像（image）的size为3X3，卷积核（kernel）的size为2X2，由此输出的特征图（Feature Map）为2X2。

$$\begin{gathered} Image=\left[\begin{array}{ccc}{i}_1& i_2& i_3\\ i_4& i_5& i_6\\ i_7& i_8& i_9\end{array}\right] \\ Kernel=\left[\begin{array}{cc}{k}_1& k_2\\ k_3& k_4\end{array}\right] \\ Feature=\left[\begin{array}{cc}{f}_1& f_2\\ f_3& f_4\end{array}\right] \end{gathered}$$
Feature的各元素由Image和Kernel计算可得：
$$\begin{gathered} f_1=i_1{k}_1+i_2{k}_2+i_4{k}_3+i_5{k}_4 \\ {f}_2=i_2{k}_1+i_3{k}_2+i_5{k}_3+i_6{k}_4 \\ {f}_3=i_4{k}_1+i_5{k}_2+i_7{k}_3+i_8{k}_4 \\ {f}_4=i_5{k}_1+i_6{k}_2+i_8{k}_3+i_9{k}_4 \end{gathered}$$
Feature和label产生的loss为：
$$Loss=\partial f_1+\partial f_2+\partial f_3+\partial f_4$$
由此BP求得的Kernel的梯度为：
$$\frac{\partial Loss}{\partial k_1}=\frac{\partial Loss}{f}\cdot \frac{\partial f}{\partial k_1}=\partial f_1{i}_1+\partial f_2{i}_2+\partial f_3{i}_4+\partial f_4{i}_5$$
$k2、k3、k4$的梯度也是类似算法。

Loss是通常是大于0的，即$\partial f_1、\partial f_2、\partial f_3、\partial f_4$一定不为0。
所以权重能否产生梯度只取决于 $i$。

那么我们来回顾实验中，权重初始化为0的两个情况：

• 模型由两层conv堆叠：权重一直为0
• 模型中仅含一层conv：权重得到更新

其实两种情况的根本差别在于Image的不同。
当只有一层conv，Image就是输入的图像，所以通常不为0。
当有两层conv，由于第一层的权重均为0，导致输入第二层的Image（就是第一层输出的Feature）均为0。由此导致conv2无法更新，回传给conv1的梯度也为0。
最终的结果就是所有层的权重均无法更新。

至此也理清了在复杂网络中，初始化为0将导致模型无法训练的根本原因了。

最后附上实验源码，希望本文能帮助到你，也欢迎讨论指正~：

import torch
import torch.nn as nn

import matplotlib.pyplot as plt


class Model(nn.Module):
	def __init__(self):
		super(Model, self).__init__()
		self.conv1 = nn.Conv2d(3, 3, 3, padding=1, bias=False)
		self.bn1 = nn.BatchNorm2d(3)
		self.conv2 = nn.Conv2d(3, 3, 3, padding=1, bias=False)
		self.bn2 = nn.BatchNorm2d(3)
		self.relu = nn.ReLU(inplace=True)

		# for m in self.modules():
		# 	if isinstance(m, nn.Conv2d):
		# 		nn.init.constant_(m.weight, 0.)

		# for m in self.modules():
		# 	if isinstance(m, nn.Conv2d):
		# 		nn.init.constant_(m.weight, 5.)

		for m in self.modules():
			if isinstance(m, nn.Conv2d):
				nn.init.kaiming_normal_(m.weight, mode="fan_in", nonlinearity="relu")

	def forward(self, x):
		x = self.conv1(x)
		x = self.bn1(x)
		x = self.relu(x)
		x = self.conv2(x)
		x = self.bn2(x)
		x = self.relu(x)
		return x


size1 = (1, 3, 224, 224)
size2 = (1, 224, 224)
image = torch.randn(size1)
label = torch.full(size2, 2, dtype=torch.long)

model = Model()
model = model.train()
optimizer = torch.optim.SGD(params=model.parameters(), lr=1e-2, momentum=0.1)
criterion = nn.CrossEntropyLoss()

losses = []
conv1_means = []
conv1_vars = []
conv2_means = []
conv2_vars = []

figure = plt.figure()
axes1 = figure.add_subplot(5, 1, 1)
axes1.set_title("loss:")
axes2 = figure.add_subplot(5, 1, 2)
axes2.set_title("conv1_means")
axes3 = figure.add_subplot(5, 1, 3)
axes3.set_title("conv1_vars")
axes4 = figure.add_subplot(5, 1, 4)
axes4.set_title("conv2_means")
axes5 = figure.add_subplot(5, 1, 5)
axes5.set_title("conv2_vars")

epochs = 40
for i in range(epochs):
	pred = model(image)

	loss = criterion(pred, label)
	loss.backward()
	losses.append(loss.item())

	conv1_weight = model.state_dict()["conv1.weight"]
	conv1_means.append(conv1_weight.mean())
	conv1_vars.append(conv1_weight.var())

	conv2_weight = model.state_dict()["conv2.weight"]
	conv2_means.append(conv2_weight.mean())
	conv2_vars.append(conv2_weight.var())
	print("round {}: loss = {}".format(i, loss.item()))

	optimizer.step()

axes1.plot(losses)
axes2.plot(conv1_means)
axes3.plot(conv1_vars)
axes4.plot(conv2_means)
axes5.plot(conv2_vars)
plt.show()