平衡二叉树类的封装实现

平衡二叉树

1.平衡二叉树： 二叉树的每一个结点的左右子树的深度差不超过1。
2.自平衡二叉树： 红黑树（R-B tree）/AVL树/替罪羊树等；
3.如何实现自平衡？

1.LL型:在左子树的左孩子上添加新结点（右旋）
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200721110347262.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1RhbmdfQUhNRVQ=,size_16,color_FFFFFF,t_70#pic_center)

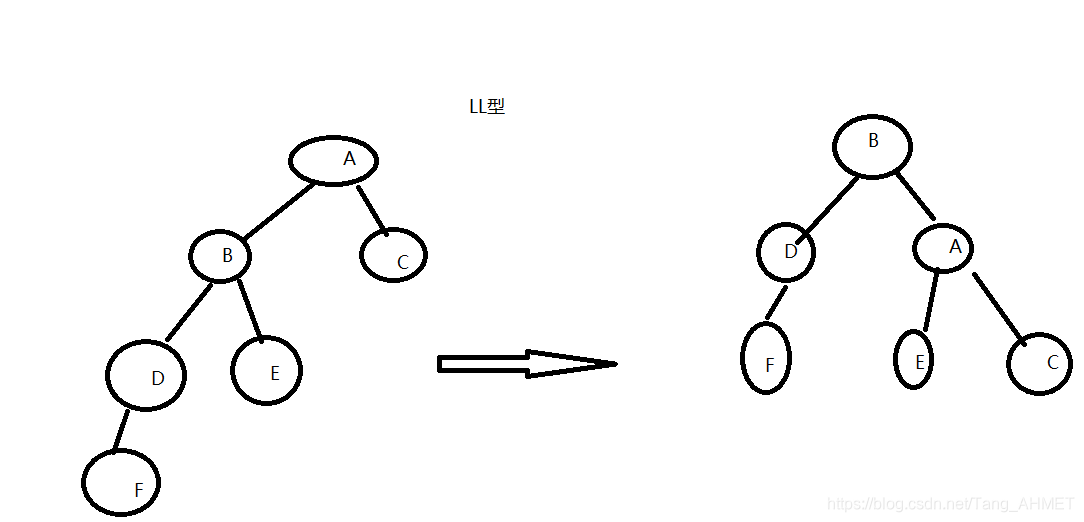
2.RR型：在右子树的右孩子上添加新结点(左旋)
3.LR型：在左子树的右孩子上添加新结点（先左旋（失衡子树）再右旋）
4.RL型：在右子树的左孩子上添加新结点（先右旋（失衡子树）再左旋）

4.STL:map(底层：红黑树)
1.插入：

 	// 1.定义map（键值对：一个键对应一个值）
    map<int,string> m; // map<键类型，值类型> 对象名;
    // 2.键值对插入
    // 第一种方式：直接赋值(相同键值覆盖）
    m[1] = "陈毓鑫";// 1号对应陈毓鑫
    m[1] = "李建杨";
    cout << m[1].c_str() << endl;
    // 第二种方式：insert（相同键值不覆盖）
    m.insert(pair<int,string>(2,"何亚飞")); // 键值对pair<键类型,值类型>(键，值);
    m.insert(pair<int,string>(2,"李建杨"));
    cout << m[2].c_str() << endl;

2.删除：

	3.删除第一组键值对
    // m.erase(m.begin());// 参数：迭代器
    // cout << m.erase(1) << endl;// 参数：键值

3：遍历

// 4.遍历所有的键值对，输出键和值
    // 第一种方式：迭代器
    map<int,string>::iterator it = m.begin();
    for(;it != m.end();++it)
    {
       pair<int,string> p = *it;
        // p.first：键
        // p.second：值
        cout << p.first << endl;
        cout << p.second.c_str() << endl;
    }
    
    // 第二种方式：泛型for
    for(pair<int,string> p : m)
    {
        cout << p.first << endl;
        cout << p.second.c_str() << endl;
    }

---

平衡二叉树实现

（二）节点类

BinaryTreeNode.h

#ifndef BinaryTreeNode_hpp
#define BinaryTreeNode_hpp
#include 
class BinaryTreeNode
{
public:
    BinaryTreeNode(int data,
                   BinaryTreeNode* pParent = nullptr,
                   BinaryTreeNode* pLeft = nullptr,
                   BinaryTreeNode* pRight = nullptr)
    :data(data),
     pParent(pParent),
     pLeft(pLeft),
     pRight(pRight)
    {
        
    }
    void preOrder();// 以当前节点为根节点的树的前序遍历
    int getHeight();// 获取以当前节点为根节点的树的深度
    void insert(const int& val);// 插入节点：小于等于根节点数据的值插入到左子树中，否则插入到右子树中
    BinaryTreeNode* remove();// 删除节点：返回删除节点处的新结点
    BinaryTreeNode* findMaxNode();// 查找左子树的最大数据节点
    BinaryTreeNode* find(const int& val);// 通过值查找节点
private:
    int data;// 数据域
    BinaryTreeNode* pLeft;// 指向左节点的指针
    BinaryTreeNode* pRight;// 指向右节点的指针
    BinaryTreeNode* pParent;// 指向父节点的指针
};

BinaryTreeNode.cpp

2.1.打印数据

void BinaryTreeNode::preOrder()
{
    // 打印当前节点的数据
    cout << this->data << "->";
    // 左子树进行前序遍历
    if(pLeft != nullptr)
    {
        pLeft->preOrder();
    }
    
    // 右子树进行前序遍历
    if(pRight != nullptr)
    {
        pRight->preOrder();
    }
}

2.2 得到树的高度

int BinaryTreeNode::getHeight()
{
    // 左子树的深度 > 右子树的深度 ？ 左子树的深度 + 1 ：右子树的深度+1；
    int lHeight = pLeft ? this->pLeft->getHeight() : 0;
    int rHeight = pRight ? pRight->getHeight() : 0;
    
    return lHeight > rHeight ? lHeight + 1:rHeight + 1;
}

2.3 插入数据

void BinaryTreeNode::insert(const int& val)
{
    // 与当前节点的值进行比较
    if(val <= this->data)
    {
        // 判断是否有左节点
        if(nullptr == pLeft)
        {
            pLeft = new BinaryTreeNode(val,this);
        }else
        {
            pLeft->insert(val);
        }
    }else
    {
        // 判读是否有右节点
        if(nullptr == pRight)
        {
            pRight = new BinaryTreeNode(val,this);
        }else
        {
            pRight->insert(val);
        }
    }
}

2.4.删除数据

BinaryTreeNode* BinaryTreeNode::remove()
{
    // 叶子节点
    if(nullptr == pLeft && nullptr == pRight)
    {
        // 判断当前节点是父节点的左节点还是右节点
        if(pParent != nullptr)
        {
            if(pParent->pLeft == this)
            {
                pParent->pLeft = nullptr;
            }else
            {
                pParent->pRight = nullptr;
            }
        }
        // 释放当前节点
        delete this;
        return nullptr;
    }else if(nullptr == pLeft || nullptr == pRight) // 当前节点有右节点
    {
        BinaryTreeNode* pNode = pLeft ? pLeft : pRight;// 要替换的节点
        if(pParent != nullptr)
        {
            if(pParent->pLeft == this)
            {
                pParent->pLeft = pNode;
            }else
            {
                pParent->pRight = pNode;
            }
        }
        delete this;
        return pNode;
    }else // 度为2的节点
    {
        // 查找当前节点的左子树中值最大的节点
        BinaryTreeNode* pMax = findMaxNode();
        // 替换数据
        data = pMax->data;
        // 递归删除pMax节点
        pMax->remove();
        return this;
    }
}

2.5：查找最大节点

BinaryTreeNode* BinaryTreeNode::findMaxNode()
{
    BinaryTreeNode* pNode = pLeft;
    while(pNode->pRight != nullptr)
    {
        pNode = pNode->pRight;
    }
    
    return pNode;
}

2.6：根据数据查找节点

BinaryTreeNode* BinaryTreeNode::find(const int& val)
{
    // 与根节点的值进行比较
    BinaryTreeNode* pNode = this;
    while(pNode != nullptr)
    {
        if(val < pNode->data)
        {
            pNode = pNode->pLeft;
        }else if(val > pNode->data)
        {
            pNode = pNode->pRight;
        }else
        {
            return pNode;
        }
    }
    
    return nullptr;
}

（3）实现树类

BinaryTree.h

#ifndef BinaryTree_hpp
#define BinaryTree_hpp

#include 
#include "BinaryTreeNode.h"
class BinaryTree
{
public:
    BinaryTree()
    :pRoot(nullptr)
    {
        
    }
    
    void insert(const int& val);
    
    
    void preOrder()
    {
        if(pRoot != nullptr)
        {
            pRoot->preOrder();
        }
    }
    
    void remove(const int& val);
private:
    BinaryTreeNode* pRoot;// 指向根节点
};

#endif /* BinaryTree_hpp */

3.1 插入

 void insert(const int& val)
    {
        // 判读根节点是否为空
        if(nullptr == pRoot)
        {
            pRoot = new BinaryTreeNode(val);
        }else
        {
            pRoot->insert(val);
        }
    }

3.2 删除

void BinaryTree::remove(const int& val)
{
    // 查找要删除的节点
    BinaryTreeNode* pDel = pRoot->find(val);
    
    if(pDel != nullptr)
    {
        // 判断要删除的是不是根节点
        if(pDel == pRoot)
        {
            pRoot = pRoot->remove();
        }else
        {
            pDel->remove();
        }
    }
}

（4）主函数测试类

int main(int argc, const char * argv[]) {
    
    BinaryTree tree;
    tree.insert(5);
    tree.insert(3);
    tree.insert(-1);
    tree.insert(10);
    tree.insert(7);
    tree.insert(-9);
    tree.insert(0);
    tree.insert(2);
    
    tree.preOrder();
    cout << endl;
    
    tree.remove(-9);
    tree.preOrder();
    cout << endl;
    
    tree.remove(10);
    tree.preOrder();
    cout << endl;
    
    tree.remove(5);
    tree.preOrder();
    cout << endl;
    return 0;
}