PCA（主成分分析）获取BoundingBox&代码分析

引言

最近要用到PCA获取目标点云的BoundingBox，但是网上给出的有关PCA的代码大都太简洁了，我觉得可能是大佬觉得比较简单，没有详细描述。这里记录一下自己的探究结果，方便大家理解。欢迎留言讨论，如有错误，请批评指正。

理论

PCA(Principal Component Analysis)是一种十分常用的数据降维方法，其主要思想是通过线性变换的方法，将一组高维数据投影成互不相关的低维数据，保留原始数据最关键、最具代表性的数据，以压缩数据量、加速运算过程。

通过问题概述PCA推导过程：

1. PCA的目标是对原始数据进行降维，怎么降维呢？
   由于数据是基于一组N维正交基表示的，因此可以将原始数据进行重新投影，投影到新的一组K维正交基上，当K

2. 那么新的正交基需要满足哪些条件呢？
   为了最大程度保留原始数据的信息，需要使降维以后的数据尽可能的分散。也就是说，新的正交基需要保证降维数据的分散程度达到最大。而数据的分散程度通常使用方差来描述，即新的正交基要保证降维后数据的方差和达到最大。当然，还需要保证基之间相互正交。

3. 具体怎么求呢？
   在实际求目标正交基的时候，需要同时保证降维后数据的方差和最大、基之间相互正交。在数学上，数据的协方差矩阵的对角线元素描述的是数据的方差，非对角线元素描述的是数据的协方差，即变量之间的相互关系。因此上述两条件可以统一到协方差矩阵里，而且降维前后协方差矩阵满足关系：$D=PC{P}^T$，$D$为降维后数据协方差矩阵，$C$为原数据协方差矩阵。因此，目标就变成了求解矩阵$P$，使得上述等式中$D$为对角阵（对$C$进行对角化），且$P$为$PC{P}^T$中最大的前$K$个（保证方差和最大）对角线元素对应的特征向量组成的矩阵。

4. 算法步骤
   1）求原数据协方差矩阵$C=1/m\ast X{X}^T$；
   2）求出协方差矩阵$C$的特征值及对应的特征向量；
   3）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前$K$行组成矩阵；
   4）$Y=PX$即为降维到$K$维后的数据.

PCA详细理论介绍，可参考如下博客，讲解的十分清楚：

• PCA的数学原理
• 主成分分析（PCA）原理总结
• 线性代数之主成分分析(PCA)算法
• 主成分分析(PCA)原理及推导–参考其拉格朗日求解法

代码

环境：Win10+VS2015+PCL1.8

代码流程：

• 导入点云–>计算质心和协方差矩阵–>计算主方向(即特征向量)；
• 将点云转到参考坐标系，保证点云主方向与参考坐标系坐标轴重合；
• 计算转换后点云的边界值(min_pt、max_pt)–>计算BoundingBox形心(mean_diag)–>将mean_diag转换到原点云；
• 最后根据变换关系及形心位置addCube()，在原点云形心处添加BoundingBox。

其实，在流程中的第一步就已经完成了点云主方向的计算，后续过程只是为了保证BoundingBox能完整的包围点云。

#include          
VTK_MODULE_INIT(vtkRenderingOpenGL);
VTK_MODULE_INIT(vtkInteractionStyle);
VTK_MODULE_INIT(vtkRenderingFreeType);

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;
typedef pcl::PointXYZ PointType;

int main(int argc, char **argv)
{
	// 导入点云
	pcl::PointCloud<PointType>::Ptr original_cloud(new pcl::PointCloud<PointType>());
	
	std::string fileName("lamppost.pcd");
	pcl::io::loadPCDFile(fileName, *original_cloud);

	// PCA：计算主方向
	Eigen::Vector4f centroid;							// 质心
	pcl::compute3DCentroid(*original_cloud, centroid);	// 齐次坐标，（c0,c1,c2,1）
	
	Eigen::Matrix3f covariance;	
	computeCovarianceMatrixNormalized(*original_cloud, centroid, covariance);		// 计算归一化协方差矩阵
	
	// 计算主方向：特征向量和特征值
	Eigen::SelfAdjointEigenSolver<Eigen::Matrix3f> eigen_solver(covariance, Eigen::ComputeEigenvectors);
	Eigen::Matrix3f eigen_vectors = eigen_solver.eigenvectors();
	//Eigen::Vector3f eigen_values = eigen_solver.eigenvalues();
	eigen_vectors.col(2) = eigen_vectors.col(0).cross(eigen_vectors.col(1));	// 校正主方向间垂直（特征向量方向： (e0, e1, e0 × e1) --- note: e0 × e1 = +/- e2）
	
	// 转到参考坐标系，将点云主方向与参考坐标系的坐标轴进行对齐
	Eigen::Matrix4f transformation(Eigen::Matrix4f::Identity());
	transformation.block<3, 3>(0, 0) = eigen_vectors.transpose();										// R^(-1) = R^T
	transformation.block<3, 1>(0, 3) = -1.f * (transformation.block<3, 3>(0, 0) * centroid.head<3>());	// t^(-1) = -R^T * t

	pcl::PointCloud<PointType> transformed_cloud;	// 变换后的点云
	pcl::transformPointCloud(*original_cloud, transformed_cloud, transformation);

	PointType min_pt, max_pt;						// 沿参考坐标系坐标轴的边界值
	pcl::getMinMax3D(transformed_cloud, min_pt, max_pt);
	const Eigen::Vector3f mean_diag = 0.5f*(max_pt.getVector3fMap() + min_pt.getVector3fMap());	// 形心

	// 参考坐标系到主方向坐标系的变换关系
	const Eigen::Quaternionf qfinal(eigen_vectors);
	const Eigen::Vector3f tfinal = eigen_vectors * mean_diag + centroid.head<3>();

	// 显示结果
	pcl::visualization::PCLVisualizer viewer;
	viewer.addPointCloud(original_cloud);

	viewer.addCoordinateSystem();

	// 显示点云主方向
	Eigen::Vector3f whd;		// 3个方向尺寸：宽高深
	whd = max_pt.getVector3fMap() - min_pt.getVector3fMap();// getVector3fMap:返回Eigen::Map 
	float scale = (whd(0) + whd(1) + whd(2)) / 3;			// 点云平均尺度，用于设置主方向箭头大小

	// std::cout << "width/heigth/depth：" << whd << endl;

	PointType cp;			// 箭头由质心分别指向pirncipal_dir_X、pirncipal_dir_Y、pirncipal_dir_Z
	cp.x = centroid(0);
	cp.y = centroid(1);
	cp.z = centroid(2);

	PointType principal_dir_X;
	principal_dir_X.x = scale * eigen_vectors(0, 0) + cp.x;
	principal_dir_X.y = scale * eigen_vectors(1, 0) + cp.y;
	principal_dir_X.z = scale * eigen_vectors(2, 0) + cp.z;

	PointType principal_dir_Y;
	principal_dir_Y.x = scale * eigen_vectors(0, 1) + cp.x;
	principal_dir_Y.y = scale * eigen_vectors(1, 1) + cp.y;
	principal_dir_Y.z = scale * eigen_vectors(2, 1) + cp.z;

	PointType principal_dir_Z;
	principal_dir_Z.x = scale * eigen_vectors(0, 2) + cp.x;
	principal_dir_Z.y = scale * eigen_vectors(1, 2) + cp.y;
	principal_dir_Z.z = scale * eigen_vectors(2, 2) + cp.z;

	viewer.addArrow(principal_dir_X, cp, 1.0, 0.0, 0.0, false, "arrow_x");		// 箭头附在起点上
	viewer.addArrow(principal_dir_Y, cp, 0.0, 1.0, 0.0, false, "arrow_y");
	viewer.addArrow(principal_dir_Z, cp, 0.0, 0.0, 1.0, false, "arrow_z");

	// 显示包围盒，并设置包围盒属性，以显示透明度
	viewer.addCube(tfinal, qfinal, whd(0), whd(1), whd(2), "bbox");
	viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_REPRESENTATION, pcl::visualization::PCL_VISUALIZER_REPRESENTATION_WIREFRAME, "bbox");
	viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_COLOR, 1.0, 0.0, 0.0, "bbox");
	
	while (!viewer.wasStopped())
	{
		viewer.spinOnce(100);
	}
	return 0;
}

另外，还可以使用pcl中的pca接口计算点云的主方向：

// 使用pcl中的pca接口
pcl::PointCloud<pcl::PointXYZ>::Ptr cloudPCAprojection (new pcl::PointCloud<pcl::PointXYZ>);
pcl::PCA<pcl::PointXYZ> pca;
pca.setInputCloud(cloudSegmented);
pca.project(*cloudSegmented, *cloudPCAprojection);
std::cerr << std::endl << "EigenVectors: " << pca.getEigenVectors() << std::endl;	// 计算特征向量
std::cerr << std::endl << "EigenValues: " << pca.getEigenValues() << std::endl;		// 计算特征值

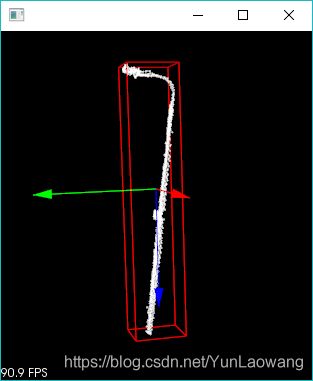
结果

点云下载地址：lamppost.pcd

分析

1. 为什么要将点云变换到原点，而不是直接对原点云进行操作？

把结论写在前面：如果只求原点云的主方向，则直接对原点云进行操作就可以了。之所以要将点云转换到原点，是为了后续能够正确的显示包围盒。原因在于getMinMax3D()计算得到的min_pt与max_pt代表的是原点坐标系下的边界值，而不是点云主方向坐标系下的值。

首先需要明确，原点云的特征向量组成了其主方向坐标系(称为$E$系)，该坐标系原点即是点云质心。同时 ，特征向量和质心坐标组成的$3\ast 4$的变换矩阵，即代表由参考坐标系(称为$W$系)到主方向坐标系的变换矩阵$T_{EW}$。

将点云从$E$系变换到$W$系，此时的点云的3个主方向已经与$W$系的坐标轴重合，同时其质心也与$W$系原点重合；在这种状态下，求点云3个方向上的边界值才是准确的。

因为pcl::getMinMax3D(*cloud, min_pt, max_pt)计算的是点云沿$W$系3个坐标轴方向上的最小、最大值，所以如果点云本身的$E$系没有与$W$系重合，即未将点云从$E$系变换到$W$系，则通过getMinMax3D()计算得到的min_pt与max_pt代表的就不是点云主方向上的边界值。

因此，如果直接对原点云进行操作，而不变换到$W$系进行操作，则得到的BoundingBox的位置和尺寸都会有偏差，其原因就在于pcl::getMinMax3D(*point_cloud_ptr, min_pt, max_pt)得到的min_pt、max_pt结果不对，对应的代码如下：

PointType min_pt, max_pt;
pcl::getMinMax3D(*point_cloud_ptr, min_pt, max_pt);	// 对原点云进行操作
const Eigen::Vector3f mean_diag = 0.5f*(max_pt.getVector3fMap() + min_pt.getVector3fMap());

// T_EW
const Eigen::Quaternionf qfinal(eigen_vectors);
const Eigen::Vector3f tfinal = mean_diag ;

参考

• PCA最小包围盒：Find minimum oriented bounding box of point cloud (C++ AND PCL)
• 网上很多相似代码的起源：Nicola Fioraio
• AABB&OBB包围盒：Moment of inertia and eccentricity based descriptors
• C++_Eigen函数库用法笔记——Block Operations