梯度提升树（GBDT）详解之二：分类举例

在2006年12月召开的 IEEE 数据挖掘国际会议上（ICDM， International Conference on Data Mining），与会的各位专家选出了当时的十大数据挖掘算法（ top 10 data mining algorithms ），可以参见文献【1】。作为集成学习（Ensemble learning）的一个重要代表AdaBoost入选其中。但基于Boosting 思想设计的算法，也是常常用来同AdaBoost进行比较的另外一个算法就是Gradient Boost。它是在传统机器学习算法里面是对真实分布拟合的最好的几种算法之一，在前几年深度学习还没有大行其道之时，Gradient Boost几乎横扫各种数据挖掘（Data mining）或知识发现（Knowledge discovery）竞赛。

 

梯度提升树（GBDT, Gradient Boosted Decision Trees），或称Gradient Tree Boosting，是一个以决策树为基学习器，以Boost为框架的加法模型的集成学习技术。在之前的文章【２】中，我们已经见识过利用GBDT进行回归分析的具体方法，希望读者在此基础之上阅读本文。

 

我们已经知道，GBDT可以用来做回归，也可以用来做分类。本文将着重介绍利用GBDT进行分类的具体方法。作为一个例子，我们将要使用的训练数据集（Train Set）如下表所示，观众的年龄、是否喜欢吃爆米花，以及他们喜欢的颜色共同构成了特征向量，而每个观众是否喜欢看科幻电影则是作为分类的标签。

就像之前我们在利用GBDT做回归时一样，作为开始，先构建一个单结点的决策树来作为对每个个体的初始估计或初始预测。之前在做回归时，这一步操作是取平均值，而现在我们要做的是分类任务，那么这个用作初始估计的值使用的就是log(odds)，这跟逻辑回归中所使用的是一样的，具体你可以参考我之前的文章【３】和【４】。

我们如何使用该值来进行分类预测呢？回忆逻辑回归时所做的，我们将其转化成为一个概率值，具体来说，是利用Logistic函数来将log(odds)值转化成概率。因此，可得给定一个观众，他喜欢看科幻电影的概率是

注意，为了方便计算，我们保留小数点后面一位有效数字，但其实log(odds)和喜欢看科幻片的概率这两个0.7只是近似计算之后出于巧合才相等的，二者直接并没有必然联系。

 

现在我们知道给定一个观众，他喜欢看科幻电影的概率是0.7 ,说明概率大于50%，所以我们最终断定他是喜欢看科幻电影的。这个最初的猜测或者估计怎么样呢？现在这是一个非常粗糙的估计。在训练数据集上，有４个人的预测结果正确，而另外两人的预测结果错误。或者说现在构建的模型在训练数据集上拟合的还不十分理想。我们可以使用伪残差来衡量最初的估计距离真实情况有多远。正如前面在回归分析时我们所做过的那样，这里的伪残差就是指观察值与预测值之间的差。

如上图所示，红色的两个点，表示数据集中不喜欢看科幻片的两个观众，或者说他们喜欢看科幻片的概率为0。类似地，蓝色的四个点，表示数据集中喜欢看科幻片的四个观众，或者说他们喜欢看科幻片的概率为１。红色以及蓝色的点是实际观察值，而灰色的虚线是我们的预测值。因此可以很容易算得每个数据点的伪残差如下：

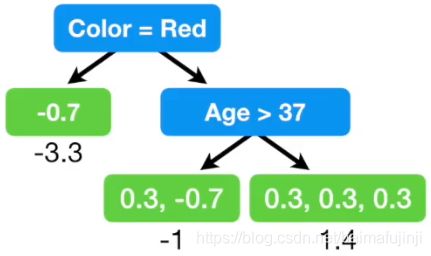
接下来要做的事情就跟之前做回归时一样了，也就是基于特征向量来构建决策树从而预测上表中给出的伪残差。于是得到下面这棵决策树。注意，我们需要限定决策树中允许之叶子数量的上限（在归回中也有类似限定），在本例中我们设定这个上限是３，毕竟这里的例子中数据规模非常小。但实践中，当面对一个较大的数据集时，通常会设定允许的最多叶子数量在8到32个之间。在使用scikit-learn工具箱时，实例化类sklearn.ensemble.GradientBoostingClassifier时，可以通过指定max_leaf_nodes来控制该值。

但如何使用上面这棵刚刚构建起来的决策树相对而言是比较复杂的。注意到，最初的估计值log(odds)≈0.7是一个对数似然，而新建的决策树叶子结点给出的伪残差是基于概率值的，因此二者是不能直接做加和的。一些转化是必不可少的，具体来说，在利用GBDT做分类时，需要使用如下这个变换对每个叶子结点上的值做进一步的处理。

上面这个变换的推导涉及到一些数学细节，这一点我们留待后续文章再做详细阐释。现在，我们基于上述公式在做计算：例如，对于第一个只有一个值-0.7的叶子结点而言，因为只有一个值，所以可以忽略上述公式中的加和符号，即有

注意，因为在构建这棵决策树之前，我们的上一棵决策树，对于所有观众给出的喜欢看科幻片的概率都是0.7，所以上述公式中Previous Probability则带入该值。于是，将该叶子结点中的值替换为-3.3。

 

接下来，计算包含0.3和-0.7这两个值的叶子结点。于是有

注意，因为叶子结点中包含有两个伪残差，因此分母上的加和部分就是对每个伪残差所对应的结果都加一次。另外，目前Previous Probability对于每个伪残差都是一样的（因为上一棵决策树中只有一个结点），但我们在生成下一次决策树时情况就不一样了。

 

类似地，最后一个结点的计算结果如下

所以现在决策树变成了如下这个样子

现在，基于之前建立的决策树，以及现在刚刚得到的新决策树，就可以对每个观众是否喜欢看科幻片进行预测了。与之前回归的情况一样，我们还要使用一个learning rate对新得到的决策树进行缩放。这里我们使用的值是0.8，出于演示方便的目的这里所取的值相对较大。在使用scikit-learn工具箱时，实例化类sklearn.ensemble.GradientBoostingClassifier时，可以通过指定参数learning_rate的值来控制学习率，该参数的默认值为0.1。

例如现在要计算上表中第一名观众的log(odds)，可得0.7 + (0.8×1.4) = 1.8。所以，利用Logistic函数计算概率得

注意到，此前我们对第一名观众是否喜欢看科幻片的概率估计是0.7，现在是0.9，显然我们的模型朝着更好的方向前进了一小步。采用上述这个方法，下面逐个计算其余观众喜欢看科幻片的概率，然后再计算伪残差，可得下表之结果

接下来，基于特征向量来构建决策树从而预测上表中给出的伪残差。于是得到下面这样一棵决策树。

再根据之前使用过的变换对每个叶子结点上的值做进一步的处理，也就是得到每个叶子结点的最终输出。

例如，我们计算上图中所示的表中第二行数据对应的叶子结点的输出

其中Previous Probability就带入上表中的概率预测值0.5。

再来计算一个稍微复杂一点的叶子，如上图所示，有四个观众的预测结果都指向该叶子结点。于是有

所以该叶子结点的输出就是0.6。这一步我们也可以看出，每个伪残差对应的分母项未必一致，这是因为上一次的预测概率不尽相同。对所有叶子结点都计算对应输出之后可得一棵新的决策树如下：

现在，我们可以把所有已经得到的组合到一起了，如下图所示。最开始，我们有一个只有一个结点的树，在此基础上我们得到了第二棵决策树，现在又有了一棵新的决策树，所有这些新生成的决策树都通过Learning Rate进行缩放，然后再加总到最开始的单结点树上。

接下来，根据已有的所有决策树，又可以算得新的伪残差。注意，第一次得到的伪残差仅仅是根据初始估计值算得的。第二次得到的伪残差则是基于初始估计值，连同第一棵决策树一起算得的，而接下来将要计算的第三次伪残差则是基于初始估计值，连同第一、二棵决策树一起算得的。而且，每次新引入一棵决策树后，伪残差都会逐渐变小。伪残差逐渐变小，就意味着构建的模型正朝着好的方向逐渐逼近。

 

为了得到更好的结果，我们将反复执行计算伪残差并构建新决策树这一过程，直到伪残差的变化不再显著大于某个值，或者达到了预先设定的决策树数量上限。在使用scikit-learn工具箱时，实例化类GradientBoostingClassifier时，可以通过指定n_estimators来控制决策树数量的上限，该参数的默认值为100。

 

为了便于演示，现在假设，我们已经得到了最终的GBDT，它只有上述三棵决策树构成（一个初始树以及两个后续建立的决策树）。如果有一个年纪25岁，喜欢吃爆米花，喜欢绿色的观众，请问他是否喜欢看科幻电影呢？我们将这个特征向量在三棵决策树上执行一遍，得到叶子结点的值，再由Learning Rate作用后加和到一起，于是有0.7+(0.81.4)+(0.80.6)=2.3。注意这是一个log(odds)，所以我们用Logistic函数将其转化为概率，得0.9。因此，我们断定该观众喜欢看科幻片。这就是利用已经训练好的GBDT进行分类的具体方法。

 

在后续的文章中，我们还将详细解释Gradient Boost的数学原理，届时读者将会更加深刻地理解算法如此设计的缘由。

 

---

参考文献

 

*本文中的例子主要参考及改编自文献【5】，文献【6】中提供了在scikit-learn中利用GBDT进行分类预测的一个简单例子。

【１】Wu, X., Kumar, V., Quinlan, J.R., Ghosh, J., Yang, Q., Motoda, H., McLachlan, G.J., Ng, A., Liu, B., Philip, S.Y. and Zhou, Z.H., 2008. Top 10 algorithms in data mining. Knowledge and information systems, 14(1), pp.1-37.

【２】梯度提升树（GBDT）详解之回归

【３】博客文章链接

【４】博客文章链接

【５】Gradient Boost for Classification

【６】https://scikit-learn.org/stable/modules/ensemble.html#gradient-tree-boosting