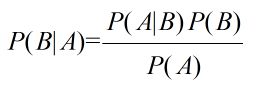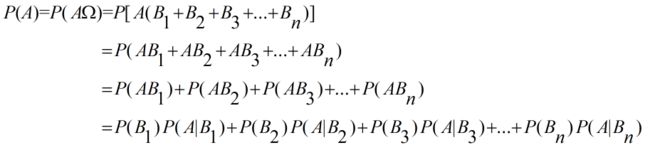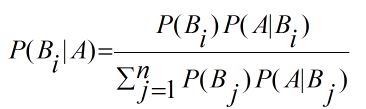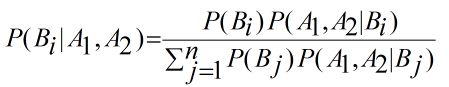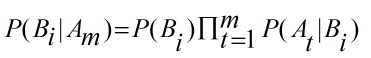朴素贝叶斯中的朴素是指特征条件独立假设, 贝叶斯是指贝叶斯定理, 我们从贝叶斯定理开始说起吧.
1. 贝叶斯定理
贝叶斯定理是用来描述两个条件概率之间的关系
1). 什么是条件概率?
如果有两个事件A和B, 条件概率就是指在事件B发生的条件下, 事件A发生的概率, 记作P(A|B).
若P(A)>0, 则满足以下公式
若P(B) > 0, 同理.
通过条件概率公式我们可以直接推出概率的乘法公式.
2). 概率的乘法公式
进而通过概率的乘法公式, 可以推出贝叶斯公式.
3). 贝叶斯公式
贝叶斯公式同样满足条件P(A)>0, P(B)>0, 在该公式中, A和B均代表单个事件, 但是当B代表一个事件组时, 公式又是如何呢?在介绍之前, 引出全概公式
4). 全概公式
当事件组B1, B2, B3, ....Bn是完备事件组(两两互不相容, 其和为全集), 并且当P(Bn) >0时, 对于任意一个事件A, 满足全概公式:
推导过程如下:
那么, 此时的完备事件组B1, B2, B3, ...Bn对于任意事件A的贝叶斯公式可写成:
上式中P(Bi)被称为先验概率, P(Bi|A)被称为后验概率.
5). 先验概率, 后验概率分别指什么呢? (举例说明)
某地区10月份下大暴雨的概率为0.9. 下大暴雨时, 发洪水的概率是0.6; 不下大暴雨时, 发洪水的概率为0.02, 试求该地区已发洪水, 下暴雨的概率?
记A1=下大暴雨, B1=发洪水, A2=不下大暴雨, B2=不发洪水, 由题意知, P(A1) = 0.9, P(B1|A1) = 0.6, P(B1|A2) = 0.02, 根据贝叶斯公式得: P(A1|B1)=0.9*0.6/[0.9*0.6 + (1-0.9)*0.02] = 0.996.
从上述例子中, 先验概率(下大暴雨的概率)很容易从现有条件中得出, 而后验概率(已经发洪水时下大暴雨的概率)需要根据附加信息用贝叶斯公式去计算得出, 下面引出百度百科对于这两者的定义.
先验概率(prior probability)是指根据以往经验和分析得到的概率,如全概率公式,它往往作为"由因求果"问题中的"因"出现的概率
后验概率是指在得到“结果”的信息后重新修正的概率,是“执果寻因”问题中的"果"。先验概率与后验概率有不可分割的联系,后验概率的计算要以先验概率为基础.
事情还没有发生,要求这件事情发生的可能性的大小,是先验概率。事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小,是后验概率。
将定义与例题相结合就能更好的理解先验概率和后验概率.
6). 如果A也是事件组时, 公式又是如何呢?
假设现有两个事件A1和A2, 公式则可改写为:
要想求满足条件A1和A2时Bi的概率, 关键在于求P(A1, A2|Bi)的概率, 在这之前需要了解事件的独立性:
通常情况下, 条件概率P(A|B)与无条件概率P(A)是不相等的, 如果P(A|B)=P(A), 则说明事件B对事件A的发生没有任何影响, 也就是说事件A与B是相互独立的, 又根据我们上面的概率乘法公式可以推出P(AB)=P(A|B)P(B)=P(A)P(B).
现假设事件A1和事件A2关于事件B独立, 根据事件的独立性, 则有P[(A1|B)(A2|B)]=P(A1|B)P(A2|B), 又由于只有在事件B这个共同条件下事件A1才会与事件A2独立, 我们不妨将式子改写为P(A1, A2|B) = P(A1|B)P(A2|B), 从而可以将我们的贝叶斯公式改写为:
假设事件组Am中的所有事件关于完备事件组Bn中任意一个事件两两相互独立, 进而公式可以推广为:
要想上式成立, 则必须要满足前提条件: 事件组Am中的所有事件关于事件组Bn的任意一个事件两两相互独立, 到这里贝叶斯定理部分就介绍完毕了,
2. 特征条件独立假设
将上面的公式应用到分类问题中, Am表示m个特征, Bn表示n个分类标签, 而要想上式成立, 要满足前提条件: m个特征关于n个分类标签中任意一个两两相互独立, 也就是特征条件独立, 而"朴素"二字表示特征条件独立假设, 即假设特征条件独立(前提条件), 想必这也就是为什么"朴素"二字恰好在贝叶斯之前.
3. 朴素贝叶斯模型
朴素贝叶斯分类模型要做的事就是在先验概率的基础上将数据集归为n个标签中后验概率最大的标签(基于最小错误率贝叶斯决策原则).
由于数据集的特征个数m和分类标签总数n是固定不变的, 即贝叶斯定理中分母不变, 所以要求最大值, 只需求出分子中的最大值, 即下式中的最大值
又可利用argmax()函数, 表示为最大值的类别, 比如X1 = argmax(f(x))表示当f(x)中的自变量x=X1时, f(x)取最大值
即求自变量Bi的值, 当Bn = Bi时, 后验概率最大, 上式也称为朴素贝叶斯推导式
通过上式, 影响最终结果的有先验概率和条件概率, 另外满足特征条件独立假设时, 上式才会成立. 即当先验概率, 条件概率和特征条件独立假设均成立时, 根据朴素贝叶斯推导式得出的结果具有真正最小错误率..
1) 先验概率
当先验概率已知时, 可以直接通过公式计算.
当先验概率未知时, 基于最小最大损失准则(让其在最糟糕的情况下, 带来的损失最小)或者N-P(聂曼-皮尔逊)决策准则来进行分类
关于这部分的具体细节可参看 https://wenku.baidu.com/view/85e559104431b90d6d85c704.html
2) 条件概率(举例说明)
现需对某产品评价中"质量好, 价格便宜, 颜值高"这三个词语作出统计, 假设它们之间两两相互独立. 已知某论坛上关于该产品的1000条评价中未购买用户概率为0.2, 未购买用户的评价中"质量好"出现0次, "价格便宜"出现100次, "颜值高"出现150次; 已购买用户的评价中"质量好"出现600次, "价格便宜"出现500次, "颜值高"出现700次, 试问评价中同时出现"质量好, 价格便宜, 颜值高"这三个词语的用户是未购买用户的概率.
首先, 特征条件相互独立, 且先验概率已知, 可直接列举出我们的公式:
事件B1表示未购买用户, 事件B2表示已购买用户, 事件A1, A2, A3则分别表示"质量好, 价格便宜, 颜值高".
由题知, P(A1|B1)=0, 分子为0, P(B1|A1, A2, A3)也就为0, 如果我们根据计算结果直接就下定义: 做出"质量好, 价格便宜, 颜值高"这个评价的用户不可能是未购买用户, 会有点以偏概全了, 比如现新有一条包含这三个词语的新评价且为未购买用户, 经询问, 该用户在体验朋友(已购买用户)的产品一段时间后, 进而在论坛作此评价. 对于此种情况, 重新计算吗?假设该用户在半个月, 一个月...后才出现, 我们要等半个月, 一个月..再计算的话, 有点不切合实际.
对于此种情况, 法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率, 所以加法平滑也叫做拉普拉斯平滑. 假定训练样本很大时, 每个分量计数加1造成的估计概率变化可以忽略不计,但可以方便有效的避免零概率问题。(参考自博文: https://www.cnblogs.com/bqtang/p/3693827.html)
应用在我们的示例中就是, P(A1|B1)=1/203, P(A2|B1)=101/203, P(A3|B1)=151/203, 进而求解即可
3) 特征条件独立假设
假设特征条件独立, 但是实际中往往不是真正独立甚至有时特征之间存在某种联系(比如年龄和星座), 这时就需通过特征选择, 主成分分析等方法尽可能让特征之间独立.