Python机器学习及实践——基础篇9（SVM回归）

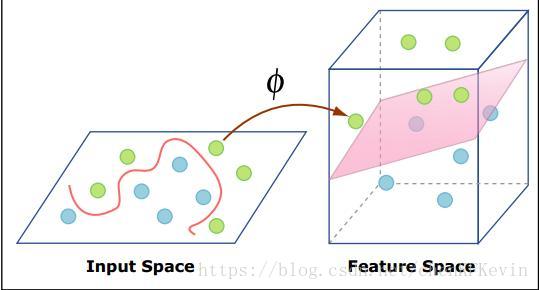
    小贴士：核函数是一项非常有用的特征映射技巧，同时在数学描述上也略为复杂。因此这里不做过度引申。简单一些理解，便是通过某种函数计算，将原有的特征映射到更高维度的空间，从而尽可能达到新的高维度特征线性可分的程度，如下图所示。结合支持向量机的特点，这种高维度线性可分的数据特征恰好可以发挥其模型优势。

    

    大家应该对基础篇3中的支持向量机（分类）中提到的分类模型的作用机理有所了解。本篇介绍的支持向量机（回归）也同样是从训练数据中选取一部分更加有效的支持向量，只是这少部分的训练样本所提供的并不是类别目标，而是具体的预测数值。

    我们继续使用上一篇分割处理好的训练和测试数据；同时我们第一次修改模型初始化的默认配置，以展现不同配置下模型性能的差异，也为后面要介绍的内容做个铺垫。

# 从sklearn.svm中导入支持向量机（回归）模型。
from sklearn.svm import SVR

# 使用线性核函数配置的支持向量机进行回归训练，并且对测试样本进行预测。
linear_svr = SVR(kernel='linear')
linear_svr.fit(X_train, y_train)
linear_svr_y_predict = linear_svr.predict(X_test)

# 使用多项式核函数配置的支持向量机进行回归训练，并且对测试样本进行预测。
poly_svr = SVR(kernel='poly')
poly_svr.fit(X_train, y_train)
poly_svr_y_predict = poly_svr.predict(X_test)

# 使用径向基核函数配置的支持向量机进行回归训练，并且对测试样本进行预测。
rbf_svr = SVR(kernel='rbf')
rbf_svr.fit(X_train, y_train)
rbf_svr_y_predict = rbf_svr.predict(X_test)

    接下来我们就不同核函数配置下的支持向量机回归模型在测试集上的回归性能作出评估。通过三组性能评测我们发现，不同配置下的模型在相同测试集上，存在非常重大的性能差异。并且在使用了径向基核函数对特征进行非线性映射之后，支持向量机展现了最佳的回归性能。 

# 使用R-squared、MSE和MAE指标对三种配置的支持向量机（回归）模型在相同测试集上进行性能评估。
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
print 'R-squared value of linear SVR is', linear_svr.score(X_test, y_test)
print 'The mean squared error of linear SVR is', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(linear_svr_y_predict))
print 'The mean absoluate error of linear SVR is', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(linear_svr_y_predict))

R-squared value of linear SVR is 0.65171709743
The mean squared error of linear SVR is 26.6433462972

The mean absoluate error of linear SVR is 3.53398125112

print 'R-squared value of Poly SVR is', poly_svr.score(X_test, y_test)
print 'The mean squared error of Poly SVR is', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(poly_svr_y_predict))
print 'The mean absoluate error of Poly SVR is', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(poly_svr_y_predict))

R-squared value of Poly SVR is 0.404454058003
The mean squared error of Poly SVR is 46.179403314

The mean absoluate error of Poly SVR is 3.75205926674

print 'R-squared value of RBF SVR is', rbf_svr.score(X_test, y_test)
print 'The mean squared error of RBF SVR is', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(rbf_svr_y_predict))
print 'The mean absoluate error of RBF SVR is', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(rbf_svr_y_predict))

R-squared value of RBF SVR is 0.756406891227
The mean squared error of RBF SVR is 18.8885250008
The mean absoluate error of RBF SVR is 2.60756329798
    本篇首次展示了不同配置模型在相同数据上所表现的性能差异。特别是除了基础篇3支持向量机（分类）模型里曾经提到过的特点之外，该系列模型还可以通过配置不同的核函数来改变模型性能。因此，建议大家使用时多尝试几种配置，进而获得更好的预测性能。