机器学习之主成分分析——基于Scikit-Learn

《Python数据科学手册》笔记

主成分分析（PCA）是一个快速灵活的数据降维无监督方法，是应用最广泛的无监督算法之一。尤其适用于数据可视化、噪音过滤、特征抽取和特征工程等领域。

用PCA降维意味着去除一个或多个最小主成分，得到一个更低维度且保留最大数据方差的数据投影。

PCA的主要弱点是经常受数据集的异常点影响。

一、“主成分”的含义

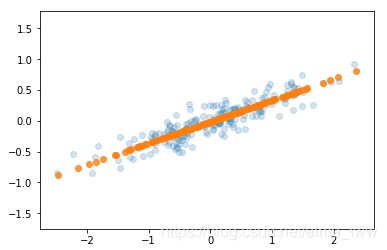
例如如下的数据点（左图），可以找出一个主轴（右图长箭头），每个数据点在主轴上的投影就是数据的主成分。

箭头长度表示输入数据中各个轴的“重要程度”，即衡量了数据投影到主轴上方差的大小，而主轴可以通过Scikit-Learn工具进行寻找。

将数据点投影到主轴上，结果如下：

由图可见，沿着最不重要的主轴的信息都被去除了，仅留下了含有最高方差值的数据成分。

二、“成分”的含义

以64像素的手写数据集为例，图像的向量表示为：x = [x1,x2,...,x64]，将向量的每个元素与对应描述的像素（单位列向量）相乘，然后将这些结果加和就是这幅图像：

image(x) = x1*(pixel 1) + x2*(pixel 2) + x3*(pixel 3) + ... + x64*(pixel 64) 

但逐像素表示方法并不是选择基向量的唯一方式，我们也可以使用其他基函数，这些函数包含预定义上的每个像素的贡献：

image(x) = mean + x1*(basis 1) + x2*(basis 2) + x3*(basis 3) + ...(按需要设置项数)

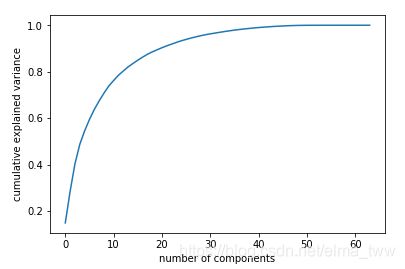
关于成分的数量，可以将累计方差贡献率看作是关于成分数量的函数，从而确定需要成分的数量。如下图：

横轴为成分数量，纵轴为累计方差，可按照精确度来选择成分数量。

三、相关代码

1. 生成散点图

（第1幅图）

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)

2.画主轴箭头

（第2幅图）

def draw_vector(v0,v1,ax=None):
    ax = ax or plt.gca()
    arrowprops = dict(arrowstyle='->',linewidth=2,shrinkA=0,shrinkB=0)
    ax.annotate('',v1,v0,arrowprops=arrowprops)
#画出数据
plt.scatter(X[:,0],X[:,1],alpha=0.2)
for length,vector in zip(pca.explained_variance_,pca.components_):
    v = vector*3*np.sqrt(length)
    draw_vector(pca.mean_,pca.mean_ + v)
plt.axis('equal')

 3.累计方差贡献率

from sklearn.datasets import load_digits
digits = load_digits()
pca = PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')