ML：非监督学习之 聚类_从KMeans到GMM高斯混合聚类

本文节选于《Python Data Science Handbook》by Jake VanderPlas 2016-11-17 First Edition

In Depth: Gaussian Mixture Model

k-means 聚类模型简单、易于理解，但是也因此无法处理比较复杂的聚类问题。尤其是它的非概率论本质，和它用简单的distance-from-cluster-center/中心点距离来进行聚类方法，导致在许多实际情况下模型效果不佳。本文要讨论的GMM/Gaussian Mixture Model可以看做是k-means的拓展，但是克服了KMeans缺点的有力工具。

Motivating GMM: Weaknesses of k-Means

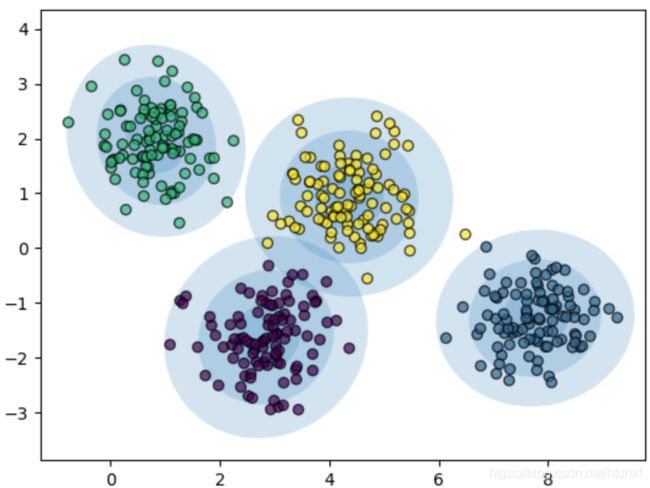
我们首先看些k-means的不足，然后想想增强聚类模型的方向。在（书的）前边我们看到，KMeans对于well-seperated的数据分类效果很棒。如下的例子，KMeans的分类结果和肉眼观察的非常接近：

# 首先生成一些数据
from sklearn.datasets import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.6, random_state=0)
X = X[:, ::-1] # 翻转坐标轴使做出来的图更直观（不翻转也差不多）

from sklearn.cluster import KMeans
kmeans = KMeans(4, random_state=0)
labels = kmeans.fit_predict(X)    # .fit_predict(X) 等价于 .fit(X).predict(X)
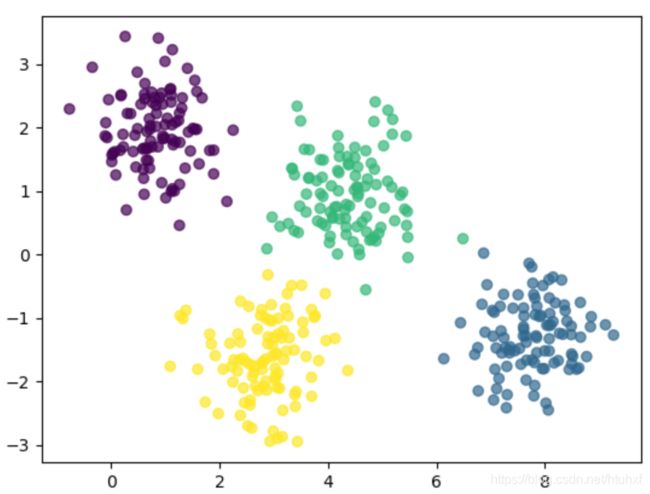
plt.scatter(X[:,0], X[:, 1], c=labels, alpha=0.7)
plt.show()

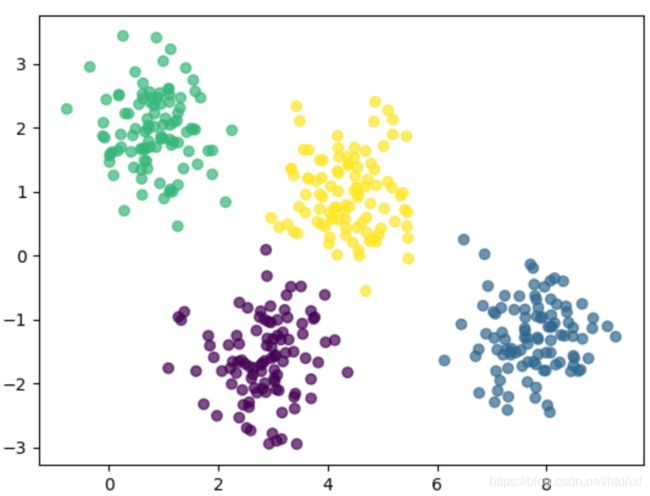如上图直观上，一些位置的数据点比其他的分类更确切一些，但是，中间的2个clusters之间的点就有些模糊，似乎归到无论哪边都说得通。同时，KMean又给不出cluster里每个点分到哪一类的概率数据，因此我们就得弄个能满足我们要求的分析工具（或许通过bootstrap来估计出来这些概率）。

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt


def plot_kmeans(kmeans, X, n_cluster=4, rseed=0, ax=None):
    labels = kmeans.fit_predict(X)

	# 先画个散点图
    ax = ax or plt.gca()
    ax.axis('equal')
    ax.scatter(X[:, 0], X[:, 1], 
    		   c=labels, alpha=0.7, ec='black', lw=1,
               cmap='viridis', s=40, zorder=2)  # zorder，计算机顺序用语，值越小越先画
	
	# 在画个圈圈
    centers = kmeans.cluster_centers_
    radii = [cdist(X[labels == i], [center]).max()
             for i, center in enumerate(centers)]
    for c, r in zip(centers, radii):
        ax.add_patch(plt.Circle(c, r,
                                fc='#CCCCCC', ec='black',
                                lw=3, alpha=0.5, zorder=1))


X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.6, random_state=0)
X = X[:, ::-1]
kmeans = KMeans(n_clusters=4, random_state=0)

plot_kmeans(kmeans, X)
plt.show()

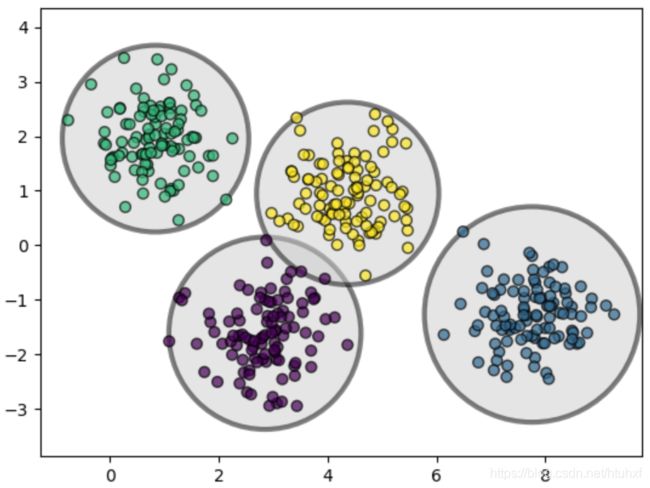上图很明显展示了KMeans是按圆圈子进行聚类的，也最适合离散分布呈现圆形的数据点。但是其他的形状就不行了，如矩形、椭圆啥的就。如下边这个例子：

import numpy as np

rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))

kmeans = KMeans(n_clusters=4, random_state=0)
plot_kmeans(kmeans, X_stretched)
plt.show()

上图直观显示了非圆形分布数据点并没有被聚好类；也形象地再次印证了在聚类上KMeans就会画圈圈这一招；

所以KMeans的两个缺点：一是适用的范围窄，二是无法给出每个数据点被聚到该某一类的概率；
我们自然会想到：如果KMeans的圆圈边界是椭圆而不局限于圆，并且是通过对比数据点到所有中心点的距离作为聚类的依据、而不是仅仅关注最近的中心是哪个，该有多好！其实满足这俩条件的模型是有的，它名字叫Guassian Mixture Models/高斯混合模型。

Generalizing E-M: Gaussian Mixture Models/GM

Gaussian Mixture模型用来对存在多维高斯概率分布特征数据进行建模。KMeans可以算是GM的一种简单情形：

from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
from sklearn.datesets import make_plobs

X, y_ture = make_plobs(n_samples=400, centers=4, 
						cluster_std=0.6, random_state=0) 
X = X[:, ::-1]

gm = Gaussian.Mixture(n_components=4)
labels = gm.fit_predict(X)

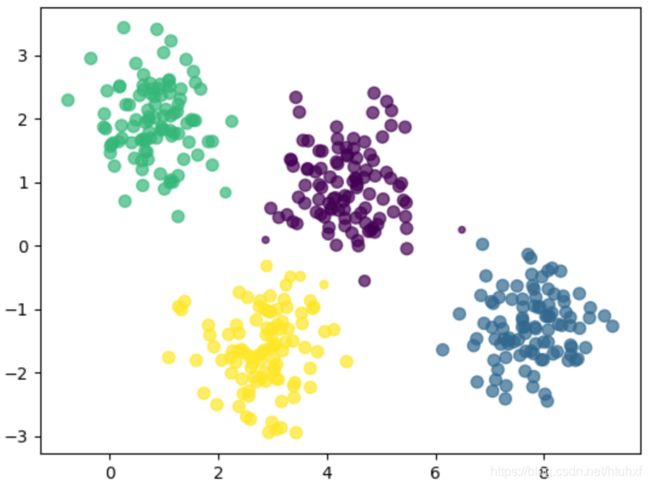
plt.scatter(X[:, 0], X[:, 1], c=labels, alpha=0.7)
plt.show()

除此之外，GM模型内含计算每个点聚到该类中心点的概率功能，predict_proba，应用如下：

probs = gm.predict_proba(X)
print(probs[:5])

# 结果如下
[[1.75162717e-22 4.69238090e-01 2.76240973e-07 5.30761633e-01]
 [4.71110558e-15 1.97106146e-17 9.99999999e-01 9.22826700e-10]
 [3.07981606e-17 2.34875746e-14 9.99999998e-01 2.09565089e-09]
 [5.00285665e-10 5.27592131e-11 9.15972926e-05 9.99908402e-01]
 [5.28028479e-14 3.86146363e-18 9.99999998e-01 1.69687673e-09]]

并且我们能够可视化每个点概率的大小

size = 50 * probs.max()
plt.scatter(X[:0], X[:1], s=size, c=labels, alpha=0.7)
plt.show()

GM的算法原理和KMeans是很相似的：使用expectation-maximization/EM/期望最大化为目标进行如下步骤：
1. Choose starting guesses for the location and shape
2. 满足条件之前进行如下循环：
a. 期望/E step：对于每一个数据点，find weights encoding the probability of membership in each cluster
b. 最大化/M step：对于每一个类，update its location, normalization, and shape based on all data points, making use of the weights

和KMeans相比它的最大特点是不同如下：

from matplot.patches import Ellipse
import matplot.pyplot as plt
from sklearn.mixture import GaussianMixture
from sklearn.datesets import make_blobs
import numpy as np

def draw_ellipse(position, covariance, ax=None, **kwargs):
	ax = ax or plt.gca()
	if covariance.shape == (2, 2):
		U, s, Vt = np.linalg.svd(covariance)
		angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
		width, height = 2 * np.sqrt(s)
	else:
		angle=0
		width, height = 2 * np.sqrt(covariance)
	
	for nsig in range(1, 4):
		ax.add_patch(Ellipse(position, nsig * width, nsig * height, 
							angle, ##kwargs))


def plot_gm(gm, X, label=True):
    labels = gm.fit_predict(X)
    if label:
        plt.scatter(X[:, 0], X[:, 1], c=labels, alpha=0.7, zorder=2,
                    ec='black')
    else:
        plt.scatter(X[:, 0], X[:, 1], alpha=0.7, zorder=2,
                    ec='black')
    plt.axis('equal')

	w_factor = 0.2 / gm.weights_.max()
	for pos, covar, w in zip(gm.means_, gm.covariances_, gm.weights_):
		draw_ellipse(pos, covar, alpha=w*w_factor)


X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.6, random_state=0)
X = X[:, ::-1]
gm = GaussianMixture(n_components=4, random_states=42)
plot_gm(gm, X)
plt.show()

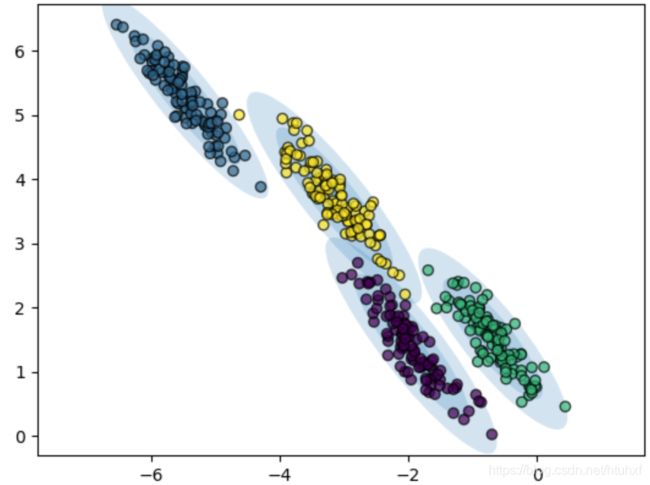
类似的，我们可以用GM模型再来模拟一下上边长条分布的数据，会发现效果好多了：

rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))

gm = GaussianMixture(n_components=4, random_state=0)
plot_gm(gm, X_stretched)
plt.show()

Choosing the covariance type

如果看sklearn.mixture.Gaussian()会发现有个选项$covariance\_type$的4个参数$\{‘full’(default),‘tied’,‘diag’,‘spherical’\}$：它们代表着不同的自由度，即决定画的椭圆朝向。
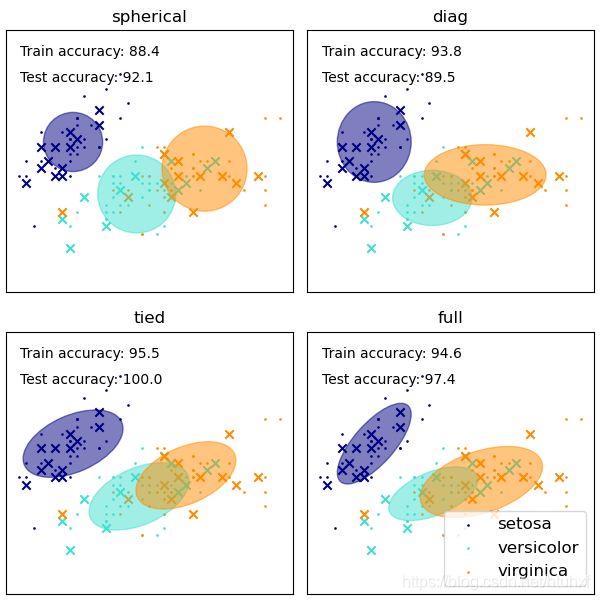
spherical：每个类的圈圈仅仅是方差不一样（表现出来就是圆的半径不同），图像和KMeans有点像（见下图），最简单、最快；
diag：每个类的圈圈的协方差矩阵都是自由独立的的对角阵，意味着圈圈的半径都平行于坐标轴但长度是自由的（见下图）；
tied：每个类的圈圈的协方差矩阵都一样，意味着圈圈大小、半径都一样，只是不要求半径方向和坐标轴平行，例如斜着的椭圆（见下图）；
full：每个类的圈圈的协方差矩阵都是自由独立的，意味着圈圈可以半径长度、和坐标轴的方向都是自由独立的（见下图）

convariance_type对应着线性变换。简单来说对角阵只是在原坐标轴方向上进行的拉伸缩短、非对角阵可以看做是拉伸缩短基础上对坐标轴也进行了旋转；
想进一步了解的可以看3Blue1Brown的非常棒非常易懂的视频展示《线性代数的本质》链接在此。

#### GM as Density Estimation
虽然GM经常被当做一种聚类的算法，但实质上它是基于density estimation/密度估计的算法。什么意思呢？就是模型对数据点的拟合技术上说不是聚类模型，而是一般意义上用于描述数据点分布的概率模型。举个栗子：

from sklearn.datasets import make_moons
import matplotlib.pyplot as plt

Xmoon, ymoon = make_moons(250, noise=0.05, random_state=0 )
plt.scatter(Xmoon[:, 0], Xmoon[:, 1], alpha=0.8, ec='black')
plt.show()

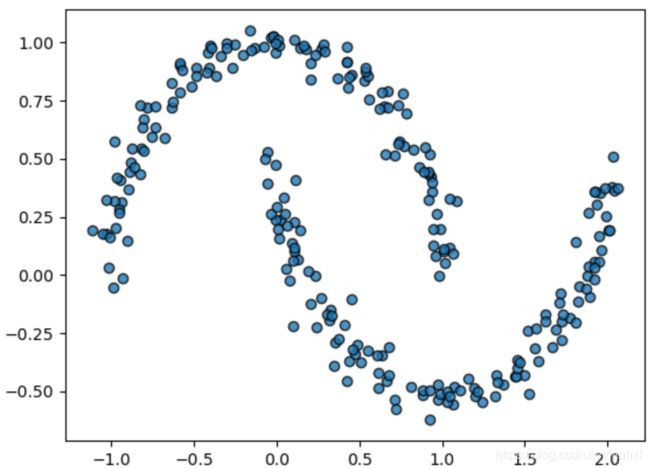如果我们直接设定n_compenents=2，结果并不理想：

from sklearn.datasets import make_moons

Xmoon, ymoon = make_moons(250, noise=0.05, random_state=0)
gm = GaussianMixture(n_components=2, random_state=0)
plot_gm(gm, Xmoon)
plt.show()

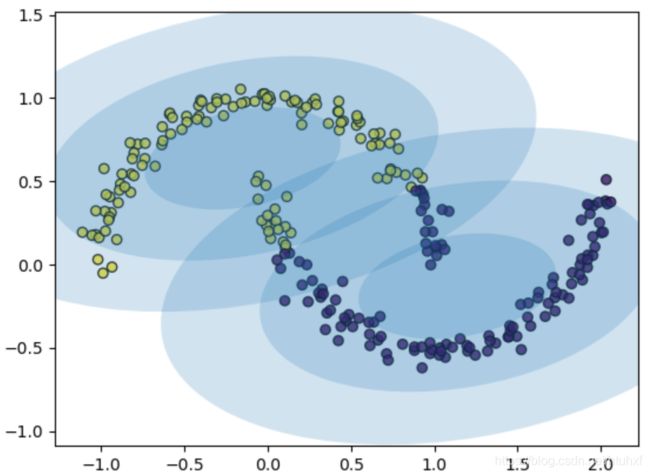但是，如果忽略标签，并且用更大的n_components，会发现：

gm = GaussianMixture(n_components=18, random_state=0)
plot_gm(gm, Xmoon, label=False)
plt.show()

上图并不是为了尽心聚类，而是拟合数据点的分布。它此时是一个分布模型，就是说我们可以用它产生类似原数据分布的新数据点，例如：

gm = GaussianMixture(n_components=18, random_state=0)
gm.fit(Xmoon)
Xnew, ynew = gm.sample(500)
plt.scatter(Xnew[:, 0], Xnew[:, 1], ec='black', alpha=0.8)
plt.show()

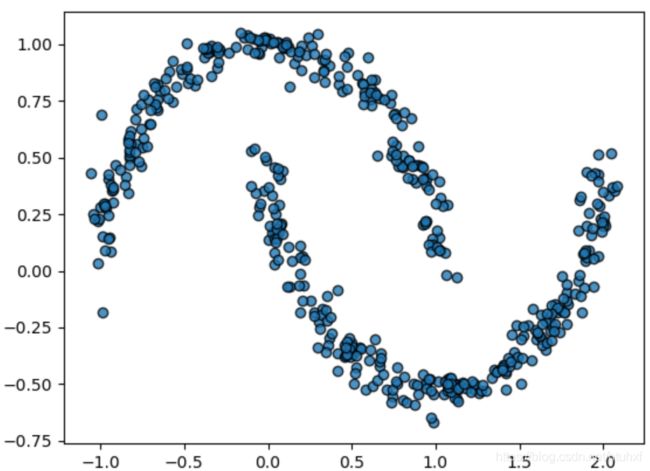对于任意的多维分布数据点集合，GM是一个方便灵活的的拟合模型。

How many components？

事实上GM作为一个generative model，提供了一些个确定最佳n_components的方法。Generative model本质上是一个拟合数据的概率分布模型， 所以我们可以轻易地量化数据点在模型里的$liklihood$，并通过cross-validation避免过拟合。另一种修正过拟合的途径是通过模型评判标准：Akaike information criterion(AIC)或者Bayesian information criterion(BIC)。Scikit-Learn的GM estimator内置AIC和BIC标准，可以非常方便的使用：

n_components = np.arange(1, 21)
models = [GaussianMixture(n, random_state=0).fit(Xmoon) for n in n_components]
plt.plot(n_components, [m.aic(Xmoon) for m in models], label='AIC')
plt.plot(n_components, [m.bic(Xmoon) for m in models], label='BIC')
plt.xlabel('n_components')
plt.legend()

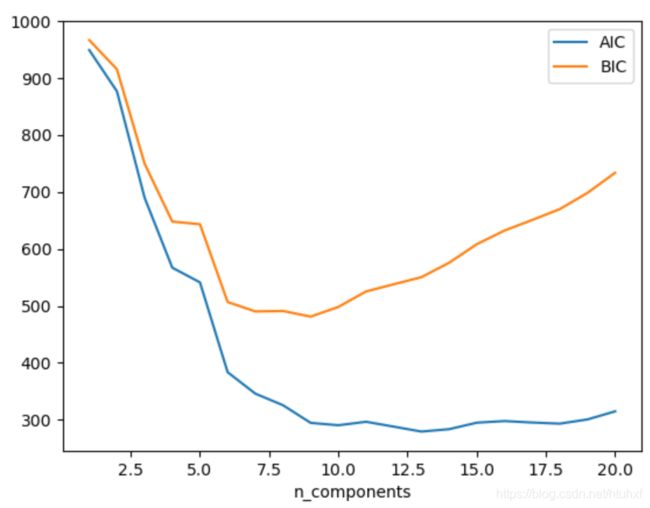AIC和BIC本质上是“熵”，即值越小越好，一般形式如下。
$$AIC=2k-2\ln (L)$$

$$BIC=k\ln (n)-2\ln (L)$$
其中$k$为模型参数个数，$n$为样本数量，$L$为极大似然函数估计。

AIC和BIC相同之处都是$L$越大越好，模型参数$k$越少，但是惩罚项的侧重不同，即当$n>e^2$即样本不小于7的时候，BIC的惩罚度更大，因为当1）其他条不变情况下，任何模型的拟合度都随着$n$的增大而增大，所以倾向于选择使用样本数较少的模型；2）只改变$k$同时$k$不小于7的情况下，AIC的结果增速较小。

需要再次强调的是，AIC和BIC选择的n_components仅针对GM作为density estimator，而不是作为聚类算法时的优选结果。不少人都更倾向于把GM作为一个density estimator，只有在简单数据集有保证的情况下用于聚类。