ML - numpy实现 PCA主成分分析

by Diwei Liu

• 原文还有PCA和LDA的区别等信息。此处仅转载PCA的Python实现部分。
• 在原文基础上有改动。

---

一、步骤简介

先把原始数据导入， 转化为m*n的矩阵，命名为XMat，再提取k个主成分，最后进行可视化。

1. 数据标准化、消除量纲影响。本例用x-E(x)做简化处理
2. 计算协方差矩阵。
3. 计算特征值和特征向量。
4. 保留最重要、即最大的k个特征值和其对应的特征向量。（通常k
5. 将m·n的矩阵，乘以n*k的特征向量，最后得到降维数据，
6. 作图输出。

– 行：代表sample，
– 列：代表feature（主成分PC是featrue的线性组合，所以k不能大于feature的个数n），PCA降维降低的是列数（即把个数多的feature，通过线性组合，降成个数少的PC），而不是行数（即向量坐标的维度）。

二、代码实现

data.txt 下载链接

• 第一步：自制PCA算法部分

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

"""
参数：
     -      XMat：原始数据矩阵
     -         k：主成分的个数   
返回值：
     - finalData：返回的低维矩阵，即(前2个)主成分矩阵
     - reconData：移动坐标轴后的矩阵，暂时没搞懂它的实际意思，所以return加了原始矩阵XMat
"""
def pca(XMat, k):
    m, n = np.shape(XMat)                          # 返回维度 m*n。本处 m*n = 150*4
    average = np.mean(XMat, axis=0)                # axis=0 返回列的平均值。
    data_adjust = XMat - average                   # 本例对数据进行的是中心化处理（也可以换成标准化）
    covX = np.cov(data_adjust.T)                   # 得到协方差矩阵
                                                   # 为什么要转置呢？转置后生成4*4的的协方差矩阵式，否则150*150。
    eigenValue, eigenVec = np.linalg.eig(covX)     # linear algebra 线性代数, eigen 特征。 |R - lambdaIp| = 0可求得p个特征根，以确定主成分，即 ∑lambda_n_of_all/∑lambda_all >=0.85。
                                                   # 得到的特征值，是从大到小排列的
    if k > n:
        print('k must be lower than feature number') 
        return
    else:
        selectVec = eigenVec[:, :k]                # 选取最大的K个特征向量。shape 是 (4, 2)
        finalData = np.dot(data_adjust, selectVec) # shape 是 (150, 2)
        reconData = np.dot(finalData, selectVec.T) + average # 为什么需要转置的原因见下边注释
    return finalData, reconData, XMat

• 注：selectVec为什么要转置？

"""第一：numpy.linalg()得到的eigenVec是这样的："""
[[eig_vector11 eig_vector21 eig_vector31 eig_vector41 ]      
 [eig_vector12 eig_vector22 eig_vector32 eig_vector42]     
 [eig_vector13 eig_vector23 eig_vector33 eig_vector43 ] 
 [eig_vector14 eig_vector24 eig_vector34 eig_vector44 ]]   
 """第二：假如是取前2大特征向量，那么 selectVec=eigenVec[:, :k]
 """
[[eig_vector11 eig_vector21]      
 [eig_vector12 eig_vector22]     
 [eig_vector13 eig_vector23] 
 [eig_vector14 eig_vector24]]  
 """因为np.dot()的运算（如下例所示），所以必须再转置回来。"""
a = np.array([[1, 1, 1],
              [2, 2, 2],
              [3, 3, 3]])
b = np.array([[1, 1],
              [1, 1],
              [1, 1]])
print(np.dot(a, b))
# 结果如下
[[3 3]
 [6 6]
 [9 9]]

numpy.ndarray类型运算规则如下：

• 选择np.cov() VS np.corrcoef():
  – 前者返回协方差矩阵，后者返回相关系数矩阵。后者其实是前者通过除以方差，消除量纲影响的矩阵 r = xy的协方差/x的方差*y的方差 = Sxy / SxSy。
  – 当数据源收量纲的影响（比如温度、产量），如果使用协方差矩阵，得到的PC即使方差贡献率很大（即特征值很大）也并不意味着它有很大的实际影响。
  – 当数据源是标准化之后的数据，那么无论用df.corr()还是np.cov(df)还是np.corrcoef(df)，得到的各个PC贡献率都是不变的。当然，特征值会（等比例）变化，特征向量也会变。

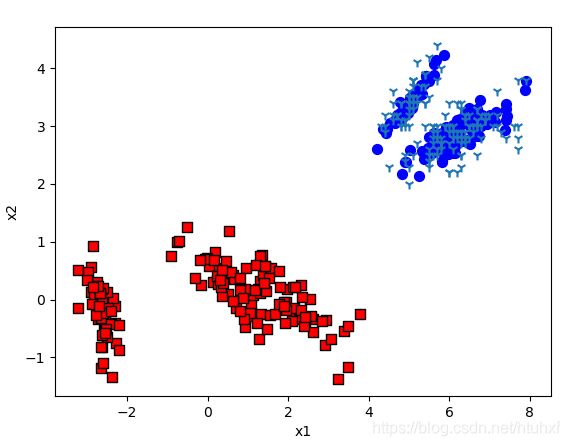
• 第二步：可视化PCA部分，即画散点图

def plotBestFit(dataArr1, dataArr2, XMat):
    m = np.shape(dataArr1)[0]
    axis_x1 = []
    axis_y1 = []
    axis_x2 = []
    axis_y2 = []
    axis_x3 = []
    axis_y3 = []
    for i in range(m):
        axis_x1.append(dataArr1[i, 0])
        axis_y1.append(dataArr1[i, 1])
        axis_x2.append(dataArr2[i, 0])
        axis_y2.append(dataArr2[i, 1])
        axis_x3.append(XMat[i, 0])
        axis_y3.append(XMat[i, 1])
        
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(axis_x1, axis_y1, s=50, c='red', marker='s', edgecolors='black')
    ax.scatter(axis_x2, axis_y2, s=50, c='blue')
    ax.scatter(axis_x3, axis_y3, s=50,  marker='1')
    
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.savefig('pathe/pic_name.png')
    plt.show()

• 第三步：定义并执行main函数部分

def main():
    XMat = np.array(pd.read_csv('path/data_name.txt', sep='\t', header=None)).astype(np.float)
    k = 2
    return pca(XMat, k)


if __name__ == '__main__':
    finalData, reconMat, XMat = main()
    plotBestFit(finalData, reconMat, XMat)

备注：

• np.array(DataFrame).astype() v.s. np.array(DataFrame)（stackoverflow链接）
  – 如果DataFrame的数字类型是INT，.astype(np.float)会把它转为float64，如果DataFrame已经是float类型，那么两者就没有什么区别。
  – PS：np.float默认是 float64，python的floats也是默认float64。

• 第四：结果输出
  蓝色圆点部分为重构后的原始数据，红色方框为提取后的二维特征，剩下的树杈为原始数据
  
• 第五：备注部分

---

其实PCA的本质就是对角化协方差矩阵。有必要解释一下为什么将特征值eigenValue按从大到小排序后再选。首先，要明白特征值表示的是什么：跳出线性代数 Linear Algebra范涛的话，它代表什么呢？

• 对一个n*n的对称矩阵进行分解，我们可以求出它的特征值和特征向量，就会产生n个n维的正交基，每个正交基会对应一个 eigen value。之后把矩阵投影到这n个正交基上，此时特征值的模就表示矩阵在该基的投影长度。eigen value越大，说明矩阵（样本）在对应的特征向量上，投影后的方差越大、样本点越离散、越容易区分，信息量也就越多。 因此，eigen value对应的特征向量eigen vector上所包含的信息量就越多，如果某几个eigen value很小，那么说明在该方向的信息量非常少，我们就可以删除小eigen value对应方向的数据，只保留大eigen value方向对应的数据，这样做以后数据量减少，但有用的信息量都保留下来了。PCA就是这个原理。

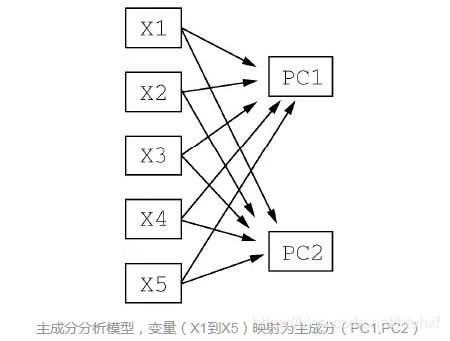
更具体的说，PCA（Principal Component Analysis）是在损失很小信息的前提下把多个指标转化为几个不相关的综合指标（Principal Component / PC），即每个PC都是原始标量的线性组合，且PC之间互不相关，使得PC比原始变量具有某些更优越的新能，从而达到简化系统结构，抓住问题的目的。

参考信息：

• 【A Beginner’s Guide to Eigenvectors, Eigenvalues, PCA, Covariance and Entropy】
• 【视频线性代数 - 系列合集（中英）】
• 【主成分分析（Principal components analysis）-最大方差解释】