数据竞赛入门系列——天池二手车交易价格预测【2】数据分析——EDA
数据竞赛入门系列——天池二手车交易价格预测【2】数据分析——EDA
- 一、介绍
- 二、数据集观察
- 2.1 加载数据
- 2.2 数据形状总览
- 2.2.1 训练集形状
- 2.2.2 测试集形状
- 2.3 数据集统计量总览
- 三、数据集的缺失和异常处理
- 3.1 查看缺失值情况
- 3.2 查看异常值检测
- 四、数据集分布情况
- 五、数据集特征分析
- 5.1 类别特征分析
- 5.2 数字特征分析
- 5.2.1 相关性分析
- 5.2.2 查看几个数值特征的偏度和峰度
- 5.2.3 数字特征相互之间的关系可视化
- 5.2.4 多变量互相回归关系可视化
- 六、生成数据报告
- 七、总结
一、介绍
本系列是记录我参加Datawhale入门数据竞赛过程中的内容和一些体会。希望能够提高自己!
竞赛为天池二手车交易价格预测。
整个系列分为五部分内容:
- 赛题理解
- 数据分析
- 特征工程
- 建模调参
- 模型融合
此为系列的第二部分,通过对数据的分析,来为后面的特征工程做好准备。本文将会从以下几个方面来记录:
- 数据集观察
- 数据集的缺失和异常处理
- 数据集分布情况
- 数据集特征分析
- 生成数据报告
就让我们开始吧!
二、数据集观察
数据探索在机器学习中我们一般称为EDA(Exploratory Data Analysis):是指对已有的数据(特别是调查或观察得来的原始数据)在尽量少的先验假定下进行探索,通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法。
2.1 加载数据
首先,需要导入各种数据科学和可视化库,并载入数据,具体代码如下:
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno
path = 'E:/JupyterNotebookProgram/Untitled Folder/'
Train_data = pd.read_csv(path+'used_car_train_20200313.csv', sep=' ')
Test_data = pd.read_csv(path+'used_car_testA_20200313.csv', sep=' ')
这里除了常用的numpy、pandas、matplotlib库之外,还使用了seaborn和missingno库。其中seaborn是一个可以理解成为更为简便的matplotlib的库,而missingno是“缺失值可视化处理”库,方便我们直接观察缺失值。
2.2 数据形状总览
2.2.1 训练集形状
首先要对导入的数据集的形状有一个大致的了解,下面是对训练集的浏览:
Train_data.head().append(Train_data.tail())
Train_data.shape
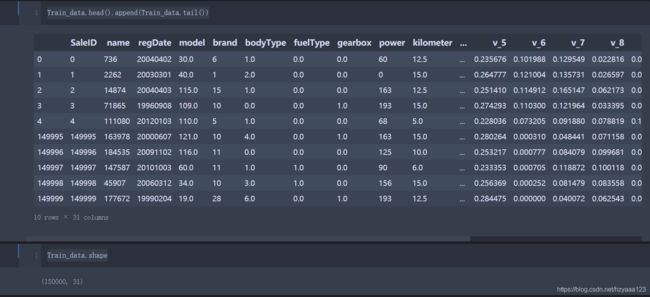
可以看到,训练数据集共有共150000个样本, 30列特征==(31列是30列特征+1列价格)==。获取数据的维度很重要,一定要首先知道数据的维度。
2.2.2 测试集形状
接下来是对测试集进行观察,观察方式与训练集相同,可以得到测试集的形状:
 测试集为50000个样本,30列特征。这里列数是30就是因为没有价格列。
测试集为50000个样本,30列特征。这里列数是30就是因为没有价格列。
为了不使内容冗长,下面的内容都不再单独描写测试集的数据情况了,只需要把代码中训练集换成测试集即可。
2.3 数据集统计量总览
-
使用describe()来了解数据集每列的统计量,包括个数(count)、平均值(mean)、方差(std)、最小值(min)、中位数(25%、50%、75%)、最大值(max)。主要用来掌握数据的大致范围,以及每个值异常值的判断。比如有时候会发现9999999 ,-1等值都是nan的另一种表达形式。
-
使用info()来了解数据每列的type,有助于了解是否存在除了nan以外的特殊符号异常。
Train_data.describe()
Train_data.info()
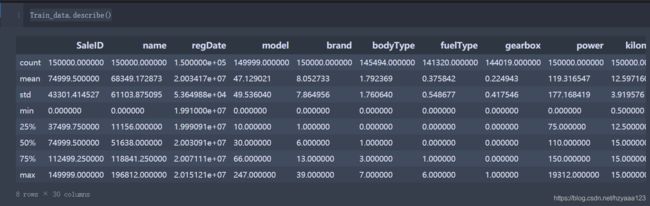
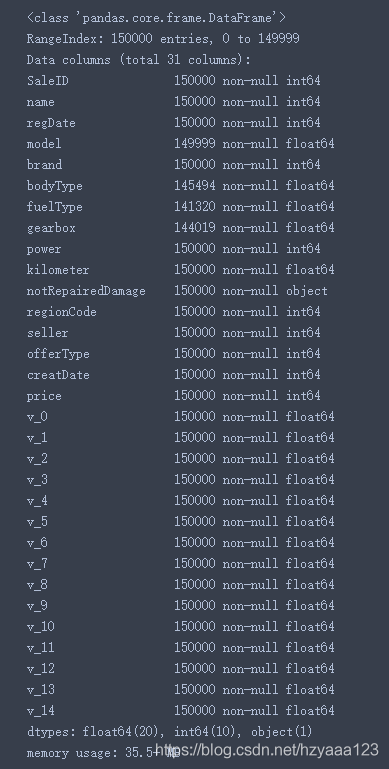
注意到有且仅有notRepairedDamage特征的类型是object,因此上面describe得到的数据统计特征里没有统计这个,所以最后describe得到的形状是8x30而不是8x31。
三、数据集的缺失和异常处理
3.1 查看缺失值情况
查看每列存在nan的情况:
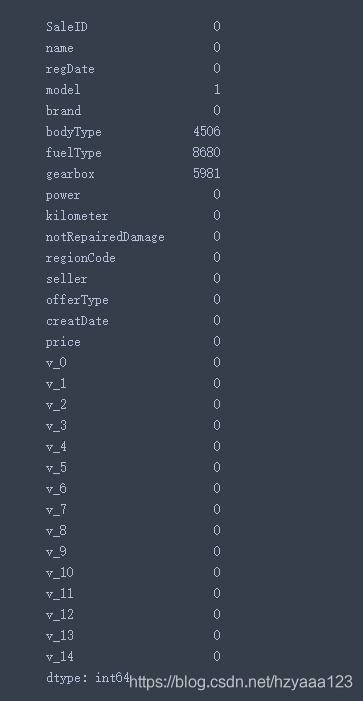
Train_data.isnull().sum()
missing = Train_data.isnull().sum()
missing = missing[missing>0]
missing.sort_values(inplace=True) # sort_values为按照指定列中数据大小排序,inplace=True为代替原数据
missing.plot.bar()
 可以很明显的看出,共有四个特征存在缺失值。如果nan的数量存在的很小一般选择填充,如果使用lgb等树模型可以直接空缺,让树自己去优化,但如果nan存在的过多、可以考虑删掉。
可以很明显的看出,共有四个特征存在缺失值。如果nan的数量存在的很小一般选择填充,如果使用lgb等树模型可以直接空缺,让树自己去优化,但如果nan存在的过多、可以考虑删掉。
接下来另缺失值可视化:
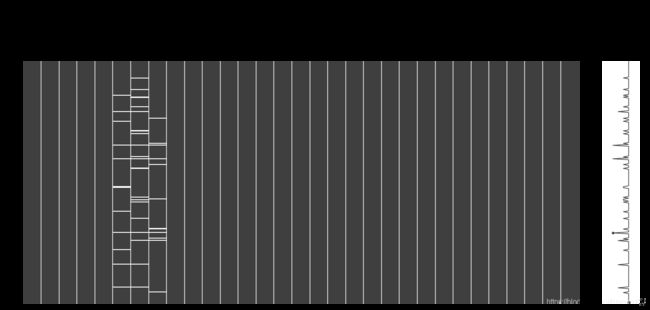
# 可视化看下缺省值
msno.matrix(Train_data.sample(250)) # sample(250)表示抽取样本中的250个样本。
3.2 查看异常值检测
我们这里先查看’notRepairedDamage’这一个特征的情况,因为它是一个object类型。
Train_data['notRepairedDamage'].value_counts() # 这里的即0的个数、空缺值的个数、1的个数
 这里的**-**为缺失值,因为很多模型对nan有直接的处理,因此先替换成nan。
这里的**-**为缺失值,因为很多模型对nan有直接的处理,因此先替换成nan。
Train_data['notRepairedDamage'].replace('-', np.nan, inplace=True) # 将'-'替换成nan
然后得到的结果为:

可以看到==-==已经没有了。
注意,在之前的统计中,notRepairedDamage特征是没有统计到有空缺值的,在替换为nan值以后再统计,就可以得到如下的结果:
 这时notRepairedDamage特征的缺失值变为了最多!
这时notRepairedDamage特征的缺失值变为了最多!
seller和offerType特征倾斜严重,一般对预测没什么帮助,先删掉。
del Train_data["seller"]
del Train_data["offerType"]
del Test_data["seller"]
del Test_data["offerType"]
四、数据集分布情况
既然要预测价格,因此一定要在训练集内了解价格特征的分布情况。
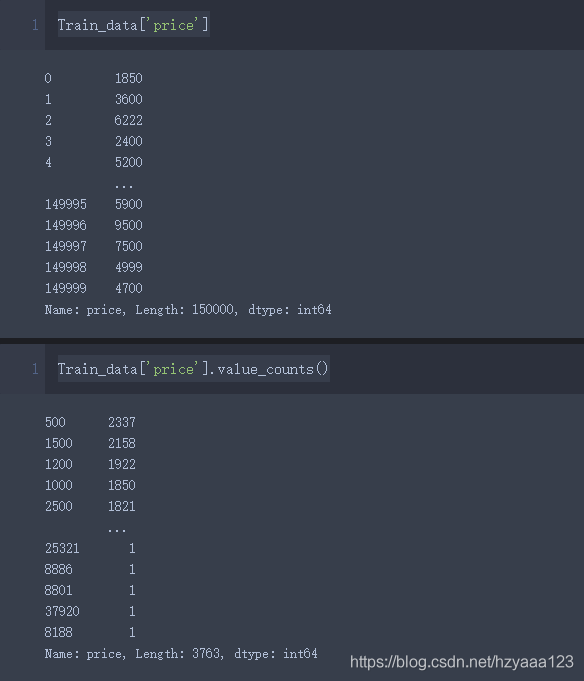
Train_data['price']
Train_data['price'].value_counts()
plt.hist(Train_data['price'], orientation='vertical', histtype='bar', color='red')
plt.show()
 可以看到,price>20000的值很少,其实可以把这些值当作异常值处理掉。
可以看到,price>20000的值很少,其实可以把这些值当作异常值处理掉。
查看price的分布情况:
import scipy.stats as st
y = Train_data['price']
plt.figure(1); plt.title('Johnson SU')
sns.distplot(y, kde=False, fit=st.johnsonsu)
plt.figure(2); plt.title('Normal')
sns.distplot(y, kde=False, fit=st.norm)
plt.figure(3);plt.title('Log Normal')
sns.distplot(y, kde=False, fit=st.lognorm)
 可以看到价格不服从正态分布,因此在进行回归之前,它必须进行转换。最佳拟合是约翰逊分布。
可以看到价格不服从正态分布,因此在进行回归之前,它必须进行转换。最佳拟合是约翰逊分布。
接下来查看价格的skewness和kurtosis:(偏度和峰度)
sns.distplot(Train_data['price'])
print('Skewness: %f' % Train_data['price'].skew())
print('Kurtosis: %f' % Train_data['price'].kurt())
plt.figure(figsize=(20,5))
plt.subplot(121)
sns.distplot(Train_data.skew(), color='blue', axlabel='Skewness')
plt.subplot(122)
sns.distplot(Train_data.kurt(), color='red', axlabel='Kurtness')
plt.hist(np.log(Train_data['price']), orientation='vertical', histtype='bar', color='red')
plt.show()
五、数据集特征分析
单独提出要预测的价格特征,并把特征分为数字特征和类别特征:
Y_train = Train_data['price']
numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13', 'v_14']
categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'regionCode',]
5.1 类别特征分析
利用nunique统计各特征中不同的值的数量:
for cat_fea in categorical_features:
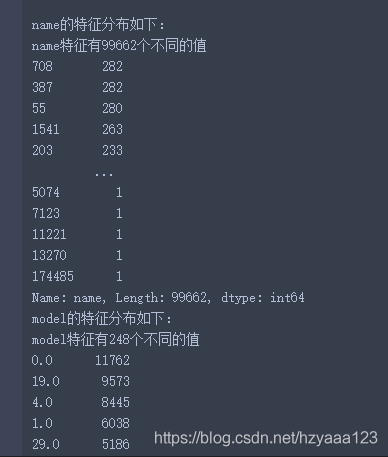
print(cat_fea + "的特征分布如下:")
print("{}特征有{}个不同的值".format(cat_fea, Train_data[cat_fea].nunique())) # nuinque()是查看该序列(axis=0/1对应着列或行)的不同值的数量。用这个函数可以查看数据有多少个不同值。
print(Train_data[cat_fea].value_counts())
注意这里是nunique而不是unique,关于后者unique的用法为:unique用法。
 类别特征的具体分析过程,包括箱形图可视化、小提琴图可视化等,不一一赘述了,详情见datawhale出的教程:Datawhale 零基础入门数据挖掘-Task2 数据分析。
类别特征的具体分析过程,包括箱形图可视化、小提琴图可视化等,不一一赘述了,详情见datawhale出的教程:Datawhale 零基础入门数据挖掘-Task2 数据分析。
5.2 数字特征分析
numeric_features.append('price')
numeric_features
Train_data.head() # 删掉了两个
5.2.1 相关性分析
# 相关性分析
price_numeric = Train_data[numeric_features]
correlation = price_numeric.corr() # 计算列的相关性,是两两变量之间的相关性
print(correlation)
print(correlation['price'].sort_values(ascending=False), '\n') # 降序排列
f, ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price', y=1, size=16)
sns.heatmap(correlation, square=True, vmax=0.8)
 颜色越淡,说明相关性越高。
颜色越淡,说明相关性越高。
关于具体什么情况适合用什么图,参见这位大佬的博客:matplotlib和Seaborn数据可视化快速入门。
5.2.2 查看几个数值特征的偏度和峰度
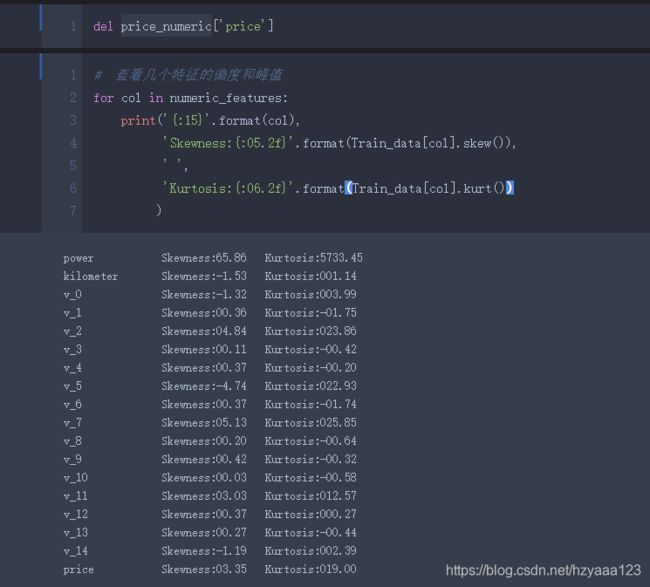
# 删除price
del numeric_train_data['price']
"""查看几个数值特征的偏度和峰度"""
for col in numeric_train_data.columns:
print('{:15}'.format(col),
'Skewness: {:05.2f}'.format(numeric_train_data[col].skew()) ,
' ' ,
'Kurtosis: {:06.2f}'.format(numeric_train_data[col].kurt())
)
"""对每个数字特征得分布可视化"""
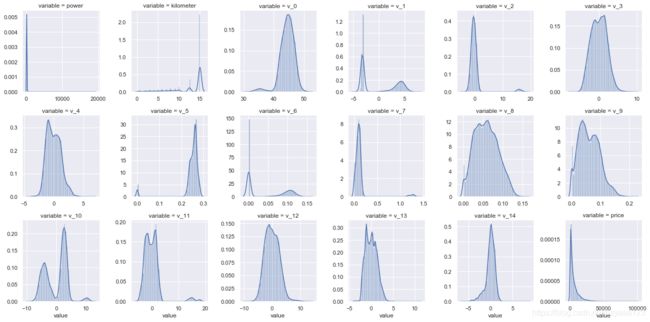
f = pd.melt(train_data, value_vars=numeric_features)
g = sns.FacetGrid(f, col="variable", col_wrap=6, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")
5.2.3 数字特征相互之间的关系可视化
sns.set()
columns = ['price', 'v_12', 'v_8', 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
sns.pairplot(Train_data[columns], size=2, kind='scatter', diag_kind='kde')
plt.show()
关于多变量之间的关系可视化的参考文章:Seaborn-05-Pairplot多变量图。
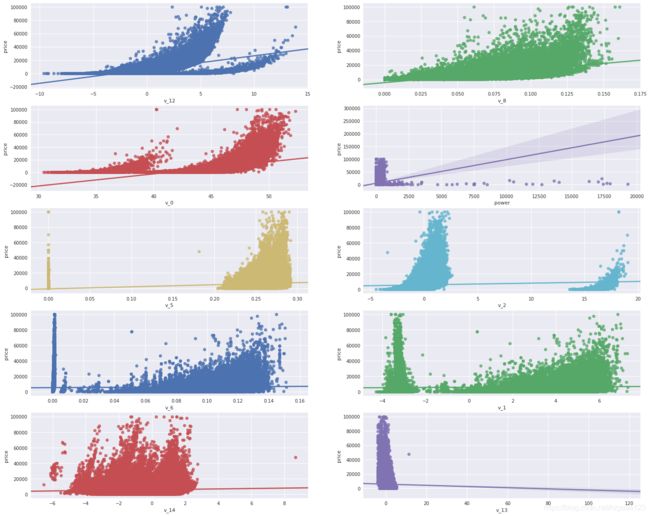
5.2.4 多变量互相回归关系可视化
#多变量互相回归关系可视化
fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6), (ax7, ax8), (ax9, ax10)) = plt.subplots(nrows=5, ncols=2, figsize=(24, 20))
# ['v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
v_12_scatter_plot = pd.concat([Y_train,Train_data['v_12']],axis = 1)
sns.regplot(x='v_12',y = 'price', data = v_12_scatter_plot,scatter= True, fit_reg=True, ax=ax1)
v_8_scatter_plot = pd.concat([Y_train,Train_data['v_8']],axis = 1)
sns.regplot(x='v_8',y = 'price',data = v_8_scatter_plot,scatter= True, fit_reg=True, ax=ax2)
v_0_scatter_plot = pd.concat([Y_train,Train_data['v_0']],axis = 1)
sns.regplot(x='v_0',y = 'price',data = v_0_scatter_plot,scatter= True, fit_reg=True, ax=ax3)
power_scatter_plot = pd.concat([Y_train,Train_data['power']],axis = 1)
sns.regplot(x='power',y = 'price',data = power_scatter_plot,scatter= True, fit_reg=True, ax=ax4)
v_5_scatter_plot = pd.concat([Y_train,Train_data['v_5']],axis = 1)
sns.regplot(x='v_5',y = 'price',data = v_5_scatter_plot,scatter= True, fit_reg=True, ax=ax5)
v_2_scatter_plot = pd.concat([Y_train,Train_data['v_2']],axis = 1)
sns.regplot(x='v_2',y = 'price',data = v_2_scatter_plot,scatter= True, fit_reg=True, ax=ax6)
v_6_scatter_plot = pd.concat([Y_train,Train_data['v_6']],axis = 1)
sns.regplot(x='v_6',y = 'price',data = v_6_scatter_plot,scatter= True, fit_reg=True, ax=ax7)
v_1_scatter_plot = pd.concat([Y_train,Train_data['v_1']],axis = 1)
sns.regplot(x='v_1',y = 'price',data = v_1_scatter_plot,scatter= True, fit_reg=True, ax=ax8)
v_14_scatter_plot = pd.concat([Y_train,Train_data['v_14']],axis = 1)
sns.regplot(x='v_14',y = 'price',data = v_14_scatter_plot,scatter= True, fit_reg=True, ax=ax9)
v_13_scatter_plot = pd.concat([Y_train,Train_data['v_13']],axis = 1)
sns.regplot(x='v_13',y = 'price',data = v_13_scatter_plot,scatter= True, fit_reg=True, ax=ax10)
六、生成数据报告
用pandas_profiling生成一个较为全面的可视化和数据报告(较为简单、方便) 最终打开html文件即可。
import pandas_profiling
pfr = pandas_profiling.ProfileReport(Train_data)
pfr.to_file("./example.html")
七、总结
数据分析对于整个的比赛过程来说还是非常有意义的,毕竟是与数据打交道,对数据越熟悉,我们后面进行特征工程就更方便一点。希望后面加油吧!